Тема 3. Статистические методы анализа взаимосвязи

Различают два типа связей между различными явлениями и их признаками: функциональную, то есть жестко детерминированную, с одной стороны, и корреляционную, статистическую — с другой.

При функциональной связи изменение признака-результата полностью обусловлено изменением признака-фактора.

При корреляционной связи изменение признака-результата обусловлено влиянием признака-фактора не полностью, а лишь в некоторой мере, так как существует еще влияние других причин, многие из которых неизвестны. Особенно это относится к взаимосвязям между социально-экономическими явлениями. Характерной особенностью корреляционной взаимосвязи является то, что она проявляется лишь на совокупности в целом и может не выполняться для отдельных ее элементов. Поэтому корреляционные зависимости изучаются по эмпирическим данным, полученным при статистическом наблюдении, так как в них отражается совокупное действие всех причин и условий на изучаемый признак.

Если исследуется зависимость признака-результата от одного фактора, то такая корреляционная связь называется парной, если факторов много, то такая корреляционная связь называется множественной. В данной контрольной работе рассматривается пример только парной корреляции. При этом признак-результат обозначим y, а признак-фактор — х.

Порядок изучения корреляционной зависимости может быть следующим:

* во-первых, на основе анализа имеющихся данных устанавливается, существует ли какая-либо зависимость между рассматриваемыми признаками;

* во-вторых, устанавливается форма, характер зависимости и мера тесноты связи;

* в-третьих, выявленная взаимосвязь описывается аналитической зависимостью.

На первом этапе анализ зависимости осуществляется на основе аналитической группировки. Так как при выполнении задания по данной теме используются те же исходные данные, то выводы, полученные в результате аналитической группировки, произведенной при выполнении задания № 1 данной контрольной работы, являются исходными для более глубокого изучения зависимости между признаками.

Так как ряд значений признака-фактора 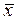и относящихся к ним групповых средних признака-результата показывает характер зависимости, то таким образом выражает в табличной форме эмпирическую функцию регрессии. Если в системе координат, где по оси (у) указываются значения признака-результата, а по оси (х) — значения признака-фактора, отметить групповые средние и соединить их прямолинейными отрезками, то полученная ломаная будет графически представлять ту же функцию. Эта линия называется эмпирической линией регрессии, которая отражает главную тенденцию рассматриваемой зависимости.

Для измерения тесноты связи применяется несколько показателей. При парной корреляции теснота связи измеряется прежде всего коэффициентом детерминации и корреляционным отношением, основанными на измерении вариации результирующего признака и ее составляющих. По теореме о разложении дисперсии:

,

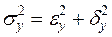где — полная дисперсия (вариация) признака-результата;

— внутригрупповая дисперсия;

— межгрупповая дисперсия.

Внутригрупповая дисперсия характеризует ту часть общей дисперсии признака-результата, которая не зависит от изменения величины признака-фактора. Тем самым она отражает влияние неучтенных причин вариации признака-результата, то есть показывает степень неопределенности. В корреляционном анализе она называется остаточной дисперсией и определяется по формуле:

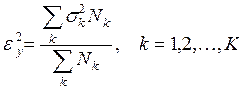
где — дисперсия признака-результата в пределах отдельной группы по признаку-фактору;

— численность отдельной группы.

Межгрупповая дисперсия отражает ту часть общей дисперсии признака-результата, которая объясняется влиянием рассматриваемого признака-фактора. Она определяется по формуле:

,

где 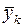— групповое среднее k -й группы.

Межгрупповая дисперсия в корреляционном анализе называется объясненной дисперсией.

Коэффициент детерминации определяется как доля объясненной дисперсии в общей дисперсии признака-результата. Он показывает, какая часть общей вариации признака-результата y объясняется влиянием изучаемого фактора х:

.

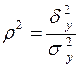Корреляционное отношение определяется как отношение средних квадратичных отклонений:

Максимально тесная связь - это связь функциональная, когда каждое значение признака-результата у может быть однозначно определено значением х, при этом остаточная дисперсия равна нулю, а коэффициент детерминации равен 1. Если связь между признаками отсутствует, то объясненная дисперсия равна 0, а следовательно, и коэффициент детерминации равен 0. Таким образом, чем ближе значение показателя к единице, тем сильнее связь между признаками.

При линейной форме зависимости (а именно линейная зависимость между признаками предполагается при выполнении задания по этой теме для упрощения расчетов) для измерения тесноты связи кроме корреляционного отношения используется также другой показатель, который называется коэффициентом корреляции. Он может быть исчислен по следующей формуле:

Коэффициент корреляции может быть рассчитан на основе корреляционной таблицы по формуле:

.

Коэффициент корреляции может принимать значения от -1 до +1.

Отрицательные значения указывают на наличие обратной (убывающей) линейной зависимости, положительные — прямой (возрастающей) линейной зависимости. Если коэффициент корреляции равен нулю, то можно сделать, вывод, что линейная связь отсутствует.

Наиболее точный результат при расчете статистических показателей может быть получен на основе обработки исходных данных, однако это значительно увеличивает объем вычислений, если объем совокупности значительный. При выполнении контрольной работы точностью расчетов можно пожертвовать ради упрощения вычислений на основе сгруппированных данных, так как целью работы является выработка навыков использования статистических методов. Однако право выбора метода расчета остается за студентом. Так, при расчете коэффициента корреляции расчеты значительно упрощаются, если осуществлять их, используя корреляционную таблицу. Она строится на основе комбинационной таблицы, полученной при выполнении задания № 1.

Следующий этап исследования корреляционной связи заключается в том, чтобы описать зависимость признака-результата от признака-фактора некоторым аналитическим выражением. Так как исследуемая зависимость является корреляционной, то функция, описывающая зависимость (аналитическое уравнение регрессии), должна быть "ближайшей" к рассматриваемой корреляционной связи. Эта задача решается на основе метода наименьших квадратов, который позволяет по исходным данным оценить параметры функции, относящейся к заданному классу. Так, если считать, что связь между исследуемыми признаками - линейная, то нужно определить параметры линейного уравнения регрессии

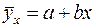
на основе системы нормальных уравнений:

Решение системы дает следующие значения параметров:

Однако определить параметры линейного уравнения регрессии можно по-другому. Существует взаимосвязь между коэффициентом (b) линейного уравнения регрессии и коэффициентом корреляции:

Помня, что средние значения признаков и их средние квадратичные отклонения были определены в предыдущем задании, коэффициент корреляции уже вычислен, можно довольно просто определить значения параметров а и b.

Задание № 3

С помощью корреляционного анализа изучить связь между признаками, указанными в Вашем варианте. Для этого:

1.Построить, эмпирическую линию регрессии.

2.Оценить тесноту связи между признаками, рассчитав коэффициент детерминации, коэффициент корреляции.

3.Найти линейное уравнение связи, график которого представить в той же системе координат, что и эмпирическая линия регрессии.

4.Интерпретировать полученные результаты, сделать выводы.

Дата добавления: 2014-12-24