Принцип, метод, алгоритм и методика измерений

Классификация измерений

Сущность основных понятий, использованных в классификации измерений, заключается в следующем.

Равноточные измерения – ряд измерений какой-либо физической величины, выполненных одинаковыми по точности средствами в одних и тех же условиях.

Неравноточные измерения – ряд измерений какой-либо физической величины, выполненных различными по точности средствами измерений и (или) в разных условиях.

Однократное измерение – измерение, выполненное один раз.

Однократное измерение иногда еще называют измерительным наблюдением. При этом предполагается, что в результате такого наблюдения получают одно значение из возможной группы значений исследуемой физической величины.

Многократное измерение – измерение одной и той же физической величины, состоящее из ряда п однократных измерений. Обычно многократным считают измерение, если п > 4, так как в этом случае результат многократного измерения может быть получен на основе статистической обработки ряда однократных измерений.

Статическое измерение – измерение физической величины, которая в процессе измерения остается постоянной во времени.

Динамическое измерение – измерение, в процессе которого размер измеряемой физической величины изменяется с течением времени. Примером динамического измерения может служить локационное измерение расстояния до быстро приближающейся цели или измерение температуры воды в процессе ее интенсивного нагревания.

Технические измерения – измерения, проводимые в заданных условиях по определенной методике, которая разработана и исследо­вана заранее, до проведения измерений. Технические измерения осуществляют для решения практических задач контроля и управления в различных областях хозяйства страны. Эти измерения носят, как правило, массовый характер. При их реализации нет необходимости определять и анализировать погрешности получаемых результатов измерений, поскольку эти погрешности заранее регламентированы соответствующими нормативными и методическими документами.

Исследовательские измерения – измерения, при которых погрешность получаемого результата оценивают по данным, полученным в процессе самого измерения или аналогичного измерения, проведенного точно в таких же условиях. Эти измерения проводят, в основном, при различных научных исследованиях, когда на первый план выступают требования высокой точности. Исследовательские измерения часто называют лабораторными, что не исключает проведение их в полевых или цеховых условиях.

Метрологические измерения – измерения, осуществляемые с целью воспроизведения единиц физических величин или передачи их размера рабочим средствам измерения. Их осуществляют при помощи эталонов и образцовых средств измерений.

Абсолютное измерение – измерение, обеспечивающее получение измеряемой величины, которая выражена в ее единицах. Примером абсолютных измерений может служить измерение длины какого-либо объекта с помощью линейки, отградуированной в миллиметрах.

Относительное измерение – измерение отношения (или изменения) величин к одноименной величине, играющей роль единицы (или принимаемой за исходную).

Прямое измерение – измерение, при котором искомое значение физической величины находят непосредственно из опытных данных. Например, измерение силы электрического тока посредством амперметра, временного интервала с помощью секундомера и т.п.

Косвенное измерение характеризуется тем, что значение искомой величины А определяют на основе известной математической зависимости F, связывающей эту величину с другими физическими величинами, значения а, которых находят чаще всего путем прямых измерений, т.е.

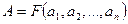(1.2)

Аргументы в формуле (1.2) иногда получают также совокупными, совместными или косвенными измерениями. Пример косвенных измерений: нахождение скорости С распространения упругих колебаний на основе прямых измерений времени t их прохождения от излучателя к приемнику и расстояния L между последними (уравнение связи С = L/t).

К косвенным измерениям обычно прибегают в тех случаях, когда прямые измерения провести невозможно или слишком сложно, либо когда косвенные измерения обеспечивают более точный результат, чем прямые.

Совокупные измерения представляют собой неоднократные, обычно прямые измерения одной или нескольких одноименных величин с получением искомого результата путем решения системы уравнений, составляемых по частным результатам измерений.

Примером совокупных измерений может служить определение взаимоиндуктивности М между двумя катушками с индуктивностями L₁ и L₂ соответственно. Если сначала соединить катушки таким образом, чтобы их магнитные поля складывались, то общую индуктивность определим по формуле

(1.3)

Соединив катушки так, чтобыих магнитные поля вычитались, для общей индуктивности будем иметь

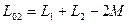(1.4)

Определив путем прямых измерений значения L ₀₁ и L ₀₂,извыражений (1.3) и (1.4), получим:

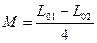(1.5)

Совместные измерения – это проводимые одновременно измерения двух или нескольких неодноименных величин с последующим вычислением искомого результата на основе зависимостей, связывающих его с указанными величинами.

Например, требуется определить зависимость сопротивления R от температуры Т, если известно уравнение связи между этими величинами

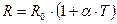(1.6)

где R ₀ – сопротивление резистора при 0 °С; 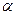– температурный коэффициент сопротивления.

Нахождение значений R ₀ и 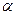сводится к измерению сопротивлений резистора R ₁ и R ₂ при двух произвольных значениях температуры Т ₁ и T ₂, соответственно и решению системы уравнений

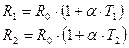(1.7)

В основе измерительного эксперимента лежат определенные принципы, а его реализация предполагает использование тех илииных методов, алгоритмов и методик.

Под принципами измерений понимают совокупность физических явлений, на которых эти измерения основаны.

Измерение одних и тех же физических величин может быть реализовано с использованием самых различных принципов, которые во многом определяют выбор средств измерений и потенциальные показатели качества последних.

Метод измерения отражает путь, способ экспериментального нахождения физической величины и представляет собой совокупность приемов использования принципов и средств измерений.

С точки зрения организации сравнения измеряемой величины с единицей измерения все методы измерения подразделяют на две группы: методы непосредственной оценки и методы сравнения.

Метод непосредственной оценки предполагает определение измеряемой величины непосредственно по отсчетному устройству измерительного прибора прямого действия, который предварительно градуируют с помощью образцовых измерительных приборов или мер. Под последними понимают средства, воспроизводящие физическую величину данного значения.

На этом методе основаны все показывающие измерительные приборы: вольтметры, амперметры, ваттметры, манометры, динамометры, термометры, тахометры и т.д.

Метод непосредственной оценки отличается быстротой получения результата измерений и обеспечивает возможность непосредственного наблюдения изменений измеряемой величины. В то же время точность измерений этим методом относительно низка.

Метод сравнения с мерой – метод измерения, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой. Этот метод позволяет получить более точные результаты измерений и имеет несколько разновидностей.

Нулевой метод – метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и величины, воспроизводимой мерой на прибор сравнения, доводят до нуля. Это достигается за счет изменения размера величины, воспроизводимой мерой.

Дифференциальный метод – метод сравнения с мерой, при котором измерительным прибором измеряется разность 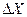между искомым значением определяемой величины Х и известным значением этой величины Х_М, воспроизводимым мерой. При этом .

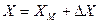Дифференциальный метод обеспечивает высокую точность измерений даже в том случае, когда точность используемого измерительного прибора относительно невелика, это достигается применением меры высокой точности, значение которой близко к значению измеряемой величины.

Еще одной разновидностью метода сравнения является метод замещения, который предполагает замещение измеряемой величины известной величиной, воспроизводимой мерой. Примером реализации метода может служить взвешивание поочередным помещением измеряемой массы груза и гирь на одну и ту же чашу весов.

К методам сравнения относят также метод совпадений, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадения отметок шкал измерительного прибора или периодических сигналов. Например, метод сравнения используют при измерении длины с помощью штангенциркуля с нониусом. Другим примером может служить измерение частоты вращения стробоскопом.

Процесс измерения значения физической величины предполагает выполнение некоторой совокупности операций. Точное предписание, определяющее порядок выполнения этих операций, носит название алгоритма измерения.

Методика измерений – порядок процесса измерений, регламентирующий методы, средства и алгоритм выполнения измерений, а также обработку их результатов, который в определенных условиях обеспечивает получение искомого результата с заданной точностью. Конкретные методики обычно регламентируются соответствующими нормативно-техническими документами, что позволяет обеспечить единство измерений. В то же время необходимо отметить, что требования к указанной регламентации для технических и исследовательских (лабораторных) измерений существенно различны. Первые требуют, как правило, жесткой метрологической, нормативной и методической базы, а вторые допускают даже принципиальные изменения в содержании методики, если эти изменения позволяют оптимизировать решение поставленной измерительной задачи.

Дата добавления: 2014-12-24