Статистическое распределение случайной величины

Случайные погрешности

Из самого названия следует, что при повторных измерениях погрешности этого типа демонстрируют свою случайную природу. Возникают они вследствие множества причин, воздействие которых на каждое отдельное измерение невозможно учесть или заранее установить. Такими причинами могут оказаться, к примеру, незначительные колебания температуры различных деталей установки, скачки напряжения, вибрации, турбулентные движения воздуха, трение в механизмах, ошибки считывания показаний приборов и т.п. Единственно возможный способ объективного учета случайных погрешностей состоит в определении их статистических закономерностей, проявляемых в результатах многократных измерений. Рассчитанные статистические оценки вносят в окончательный результат измерения.

Основным типом погрешностей являются случайные погрешности. Они поддаются строгому математическому описанию, что позволяет делать выводы о качестве измерений, в которых они присутствуют.

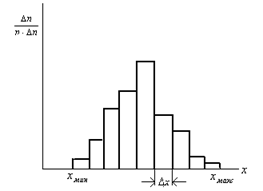Гистограмма – ступенчатая диаграмма, показывающая как часто при измерениях появляются результаты, попадающие в тот или иной интервал 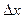между наименьшим 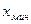и наибольшим 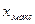из измеренных значений величины (рис.2). Гистограмма строится в следующих координатах: по оси абсцисс откладывается измеряемая величина , по оси ординат – . Здесь – полное количество проведенных измерений, 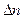– количество результатов, попавших в интервал .

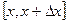Рис. 2. Гистограмма.

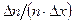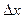Отношение есть доля результатов, оказавшихся в указанном интервале. Оно имеет смысл вероятности попадания результата отдельного измерения в данный интервал. Выражение , получаемое после деления на ширину интервала , приобретает смысл плотности вероятности.

При очень большом количестве измерений 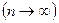весь диапазон измерения величины можно разбить на бесконечно малые интервалы 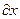, как это делается в математике, и найти количество результатов в каждом из них. В этом случае гистограмма превратится в плавную кривую – график функции

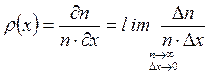(2.7)

Такую функцию называют плотностью вероятности, или распределением вероятности. Распределение выступает в роли исчерпывающей характеристики случайной величины. Закон распределения можно задать в виде функционального выражения, графика, таблицы или каким-то другим способом. Распределение содержит наиболее полную информацию о случайной величине, однако пользоваться им не всегда удобно. Оперируя результатами проведенного эксперимента, вместо функции распределения лучше иметь привычные числовые величины – ими являются среднее значение и дисперсия.

Среднее значение 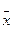измеряемой величины указывает центр распределения, около которого группируются результаты отдельных измерений

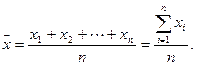(2.8)

Дисперсия вводится как средний квадрат отклонения отдельных результатов от среднего значения случайной величины

(2.9)

Среднее квадратичное отклонение (СКО), называемое также стандартным, определяется как корень из дисперсии

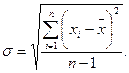(2.10)

Как следует из способа вычисления σ, эта величина характеризует разброс результатов отдельных измерений вокруг среднего значения, получаемого после обработки всех данных многократного измерения. СКО является характеристикой точности примененного метода измерения.

Связь среднего квадратичного отклонения σ_x окончательного результата (другими словами, погрешности определения среднего значения) и среднего квадратичного отклонения 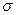отдельного измерения задается соотношением

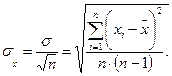(2.11)

Важным практическим выводом из (2.11), который относится к многократным измерениям, содержащим только случайные ошибки, является заключение о возможности уменьшить погрешность окончательного результата при увеличении количества отдельных измерений. Однако также следует помнить, что повышение точности не дается бесплатно. Так, чтобы повысить точность в 10 раз, количество измерений требуется увеличить в 100 раз.

Рассмотрим самый распространенный случай нормального распределения как результатов отдельных измерений . За оценку погрешности окончательного результата многократного измерения примем величину 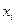, задающую симметричный относительно 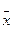интервал значений от 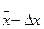до , называемый доверительным интервалом.

При небольшом числе измерений выполняется так называемое распределение Стьюдента. Случайной величиной в распределении Стьюдента является величина 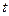, зависящая от числа измерений и уровня доверительной вероятности 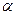. Величина t(α,n) называется коэффициентом Стьюдента, выражается следующим образом:

(2.12)

Отсюда видно, что предельная ошибка величины 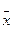при уровне доверительной вероятности 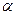выражается через коэффициент Стьюдента и среднеквадратичную ошибку арифметического среднего:

(2.13)

Для определения предельной ошибки при заданном уровне доверительной вероятности надо, прежде всего, найти среднее арифметическое результатов измерений и оценку его стандартного отклонения . По таблице (1), соответственно числу измерений и уровню доверительной вероятности, берется коэффициент Стьюдента и затем по формуле (2.13) находится .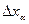

Таблица 1 – Коэффициенты Стьюдента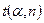

n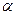
0,68	0,90	0,95	0,99	0,999
	2,0	6,31	12,70	63,70	636,6
	1,4	2,92	4,30	9,92	31,6
	1,3	2,35	3,18	5,84	12,9
	1,2	2,13	2,78	4,60	8,6
	1,2	2,02	2,57	4,03	6,9
	1,1	1,94	2,45	3,71	6,0
	1,1	1,89	2,36	3,50	5,4
	1,1	1,86	2,31	3,36	5,0
	1,1	1,83	2,26	3,25	4,8
	1,1	1,76	2,14	2,98	4,1
	1,1	1,73	2,09	2,86	3,9
	1,1	1,68	2,01	2,68	3,5
	1.0	1,66	1,98	2,63	3,4

Уровень доверительной вероятности в физическом практикуме экспериментатор выбирает сам, если в руководстве к работе нет на это специальных указаний. На практике по мировым стандартам считается достаточным уровень доверительной вероятности .

Наиболее простым, экспрессным методом оценки ошибки косвенных измерений является метод наихудшего случая. «Наихудшим» называют такой случай, когда все ошибки измерений влияют на результат измерения в одном направлении, например, увеличивают величину x. Так можно оценить верхний предел x⁺ величины x, измеряемой косвенным путем. Для этого нужно выяснить по поводу каждого аргумента в отдельности, что с ним следует делать, уменьшать или увеличивать, чтобы величина x увеличивалась.

Дата добавления: 2014-12-24