Погрешности косвенных измерений

В большинстве экспериментов используют косвенные измерения. Исследуемую величину f определяют по результатам прямых измерений других физических величин, например, x, y, z,…, с которыми она связана заранее установленным математическим соотношением

f =f (x,y,z,….) (2.15)

Эта связь должна быть известна экспериментатору. Помимо данных прямых измерений, параметрами (2.15) могут оказаться другие величины, точно заданные или полученные в других измерениях, – они составляют набор исходных данных.

Выражение (2.15), записанное в явном виде, называют рабочей формулой и используют как для оценивания результатов косвенного измерения 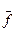, так и для оценивания погрешности измерений . Естественно, обе оценки связаны с окончательными результатами прямых измерений 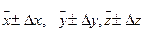,…. Обычно, чтобы получить (2.15), используют модельное описание и, во избежание модельных погрешностей при измерении f, оно должно адекватно отражать исследуемое физическое явление. Если модель точна, то модельные погрешности исключены, а косвенные измерения дают надежные результаты.

Как и в предыдущем разделе, рассмотрим случай, когда погрешности измерения величин x, y, z,… носят только случайный характер и соответствуют нормальному закону распределения. Кроме этого, погрешность каждого определенно взятого прямого измерения не зависима, т.е. не подвержена воздействию случайных факторов, вызывающих погрешности других прямых измерений, выполненных в эксперименте. Такие измерения и сами измеряемые величины носят название статистически независимых, или просто независимых. При выполнении указанных условий среднее значение величины f определяют на основе (2.15), исходя из средних значений величин x, y, z,….:

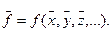(2.16)

Если точность прямых измерений достаточно высока, т.е.

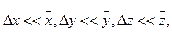…, то погрешности результатов прямых измерений переносятся на результат косвенного измерения как независимые нормальные распределения f вокруг 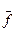по каждому из аргументов функции (2.16). Строгое обоснование этого утверждения можно найти в математической статистике. Погрешность измерения f вследствие малых случайных вариаций только величины х:

,

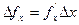только величины y – 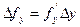, (2.17)

только величины z – 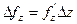, и т.д.

Здесь … – производные функции f(x,y,z,….) по соответствующим переменным, являющиеся частными производными и обозначаемые в виде …… аргументами в вычисленных производных (2.17) служат оценки средних значений …..

Совместное распределение f вокруг 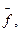которое учитывает отдельные распределения по каждому из аргументов (2.16), должно определять погрешность косвенного измерения . Эти распределения нормальны и независимы, поэтому дисперсия их совместного распределения равна сумме их дисперсий, что строго доказано в математической статистике. Тогда среднее квадратичное отклонение совместного распределения, вычисляемое как корень из дисперсии, следует находить из выражения:

(2.18)

Это выражение имеет общий характер и его можно использовать для оценивания погрешности косвенного измерения, выполненного при любом виде функции f(x,y,z,….). Однако следует твердо помнить, что при непосредственных расчетах в (2.18) необходимо поставить только погрешности 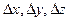…, найденные для одного и того же значения доверительной вероятности. Погрешность косвенного измерения 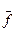так же будет соответствовать этому значению доверительной вероятности. Рекомендуется использовать значение вероятности 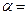0, 68.

Таблица 2 – Связь погрешностей прямых и косвенных измерений

Рабочая формула	Формула погрешности

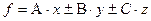
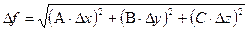
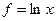
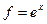
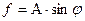
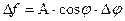
Применим (2.18) к некоторым распространенным зависимостям. Интерес представляют те случаи, когда с помощью (2.18) удается установить функциональную связь между погрешностями прямых измерений и погрешностью косвенного измерения.

В таблице №2 приняты следующие обозначения: 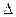– для абсолютной погрешности, 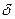– для относительной погрешности, 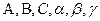– постоянные, – результаты прямых измерений, f – результат косвенного измерения.

Дата добавления: 2014-12-24