
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методологічні основи статистичного аналізу соціально-економічних явищ і процесів 1 страница
|
|
|
|
2.1 Методологія статистичних групувань. Оформлення статистичного угрупування у вигляді ряду розподілу та його графічне зображення.
Групування поділяються на прості (об’єднання одиниць сукупності в групи за однією будь-якою ознакою) і комбінаційні (розподіл сукупності на групи за двома і більше ознаками).
У групуваннях за кількісними ознаками постає питання про кількість груп і величину інтервалу. Величина інтервалу – це різниця між максимальним і мінімальним значеннями ознаки в кожній групі. Інтервали груп можуть бути рівними і нерівними. Перші застосовують тоді, коли ознака групування розподілена в сукупності більш-менш рівномірно, другі – при значній варіації розміру ознаки.
Серед методів визначення ширини рівних інтервалів розглядають метод Стреджеса та метод середнього квадратичного відхилення.
За методом Стреджеса ширину кожного інтервалу визначають за формулою 
 (2.1)
(2.1)
де Хmax, Хmin - найбільше та якнайменше значення ознаки,
m - кількість груп.
Кількість груп визначається або самостійно, або за формулою:
m = 1 + 2,30259 lg n, (2.2)
де n — обсяг сукупності;
m — число інтервалів (груп).
Визначаючи межі інтервалів, ширину h доцільно округлювати.
Надалі, шляхом добавлення величини інтервалу до мінімального значення ознаки у групі («нижньої границі»), одержують групи об'єктів за розміром аналізованої ознаки. Результати такого угрупування надаються у таблиці за формою таблиці 2.1
Таблиця 2.1 - Схема угрупування
| № групи | Межі групи | Кількість одиниць сукупності | |
| в абсолютному вираженні | % до підсумку | ||
| … | … | … | … |
| … | …. | … | … |
| Разом | 100,0 |
Таким чином, на основі групування одиниць спостереження за однією ознакою та підрахунків числа одиниць в кожній групі одержують ряд розподілу, який складається з двох елементів: варіант (окремі значення ознаки, що варіює) та частот.
Після визначення меж інтервалів формують таблицю згрупованих даних (табл. 3.1). Контрольними числами у побудованій таблиці будуть: сума стовпця “Кількості” (дорівнює обсягу вибірки N), сума стовпця “Відносні частоти” (дорівнює 1). Зазначимо, що кожен з інтервалів охоплює праву і не охоплює лівої межі, а тому деколи крайні межі дещо розширюють, щоб охопити найменші та найбільші значення.
Таблиця 2.2 - Згруповані дані для побудови гістограми
| Номер інтервалу (групи) | Межі | Кількості вимірювань | Відносні частоти | Накопичені частоти | |
| нижня | верхня | ||||
- 
| z 0 =x min | n 0 | p 0  n 0 /N n 0 /N
| F (z 0) = p 1 | |
| z 0 =x min | z 1 = z 0 +∆ | n 1 | p 1  n 1 /N n 1 /N
| F (z 1) = =F (z 0) + p 2 | |
| … | zi | zi+ 1 = zi+∆ | … | … | F (zi+ 1) = =F (pi) + pi+ 1 |
| [ k ] | zk- 1 | zk= zk- 1+  =x max =x max
| nk | pk  nk/N nk/N
| F (zk) = 1 |
Цю таблицю використовують для отримання оцінок ймовірності попадання результатів вимірювань у той чи інших інтервал (за стовпцем "Відносні частоти"), або в декілька сусідніх інтервалів (за різницею значень у стовпці "Накопичені частоти"), або ймовірності появи значень, що не перевищують (чи більші) заданого значення (теж за стовпцем "Накопичені частоти").
Графік (стовпцева діаграма), побудований за стовпцем "Відносні частоти”, називають гістограмою. Якщо сполучити середини стовпців частот, то утворена ламана буде полігоном частот (як синонім, вживають також термін " варіаційна крива "). Якщо ж сполучити середини стовпців гістограми накопичених частот, то отримаємо графік кумуляти.
2.2 Розрахунок середньої та характеристик варіації. Оцінка довірчих меж для середньої.
Середні величини використовують тоді, коли значення досліджуваної ознаки змінюються (варіюють) залежно від конкретних умов. Варіація ознак і зумовлює потребу у використанні середніх величин.
Середня величина характеризує типовий рівень варіюючої ознаки і відображує те спільне, характерне, що об’єднує всю масу елементів, тобто статистичну сукупність. Проте необхідно знати, що середня буде відображати типовий рівень ознаки лише в тому випадку, коли статистична сукупність, за якою вона обчислюється, є якісно однорідна (однотипна) і складається із значної кількості одиниць.
При вивченні масових суспільних явищ і процесів, що відбуваються на підприємствах міського господарства, найбільш часто використовують такі середні величини:
♦ арифметична:
а) проста:
 =
= 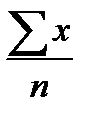 ,
,
б) зважена:
 =
= 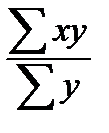 ,
,
♦ гармонійна:
а) проста:
 =
=  ,
,
б) зважена:
 =
= 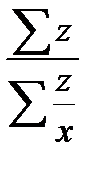 ,
, 
♦ геометрична:
а) проста:

 =
=  ,
,
б) зважена:
 =
=  ,
,
♦ хронологічна:
 =
= 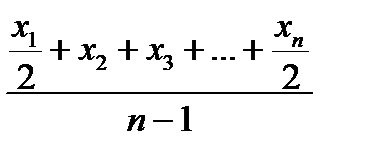 ,
,
де  – середня величина;
– середня величина;
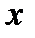 – індивідуальні значення варіюючої ознаки (варіанти);
– індивідуальні значення варіюючої ознаки (варіанти);
 – число варіант;
– число варіант;
 – частоти (ваги);
– частоти (ваги);
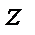 – загальний обсяг (об’єм, рівень) досліджуваної статистичної сукупності.
– загальний обсяг (об’єм, рівень) досліджуваної статистичної сукупності.
Слід зазначити, що середню арифметичну і гармонійну величину застосовують для вивчення розподілу статистичної сукупності, середню геометричну – для розрахунку середнього темпу зростання того чи іншого показника, середню хронологічну – для визначення середнього рівня динамічного ряду (моментного).
Для виміру і оцінювання варіації застосовують абсолютні й відносні показники.
До абсолютних показників варіації відносяться:
◊ розмах варіації (R) – це різниця між найбільшим (хmax) і найменшим (хmin) значеннями ознаки:
R = хmax - хmin;
◊ середнє лінійне відхилення (d) – являє собою арифметичну суму з абсолютних значень усіх відхилень індивідуальних значень ознаки від середньої:
а) просте:
d =  ;
;
б) зважене:
d =  ;
;
◊ дисперсія ( ϭ2 ) – це середня арифметична сума квадратів відхилень індивідуальних значень ознаки:
а) проста:
ϭ2 =  ;
;
б) зважена:
ϭ2 =  ;
;
◊ середнє квадратичне відхилення (δ) – його обчислюють, здобувши квадратичний корінь з дисперсії:
а) просте:
δ = 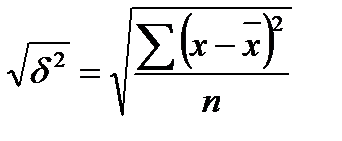 ;
;
б) зважене:
δ = 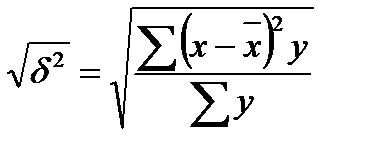 .
.
Для порівняння варіації різних ознак в одній статистичній сукупності або однієї ознаки в кількох сукупностях з різною середньою величиною використовуються відносні показники варіації (коефіцієнти), що обчислюються як відношення абсолютних показників варіації до середньої арифметичної та виражаються в відсотках.
До цих показників відносяться наступні:
♦ коефіцієнт осциляції (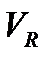 ):
):

 ;
;
♦ лінійний коефіцієнт варіації (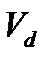 ):
):

 ;
;
♦ квадратичний коефіцієнт варіації ( ):
):
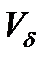
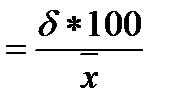 .
.
Найбільш широке використання отримав квадратичний коефіцієнт варіації, який застосовується в якості критерію оцінки ступеня однорідності сукупності.
Чим більший коефіцієнт варіації, тим менш однорідна статистична сукупність і тим менш типова середня для даної сукупності. Розрізняють такі значення відносних коливань:
* незначне коливання при 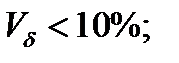
* середнє коливання при 



* велике коливання при 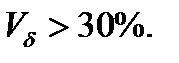
Вважають, що сукупність є однорідною, а середня – типовою, коли квадратичний коефіцієнт варіації не перевищує 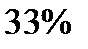 .
.
Враховуючи, що аналіз показників буде проводитися за вибірковими даними, визначають поняття довірчих меж показника, у тому числі наводять відповідні формули. Так межі довірчого інтервалу для середньої визначаються на основі точкової оцінки та граничної помилки вибірки  . Наприклад, для факторного показника визначення довірчих меж ввідбувається наступним чином:
. Наприклад, для факторного показника визначення довірчих меж ввідбувається наступним чином:
 ; (2.3)
; (2.3)
де m — стандартна (середня) помилка вибірки (необхідно надати її поняття);
t — квантиль розподілу ймовірностей (коефіцієнт довіри, що відповідає ймовірності g).
Величину стандартної помилки можна визначити за формулою для відбору:
повторного 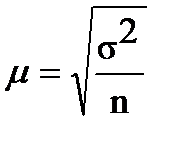 (2.4)
(2.4)
без повторного 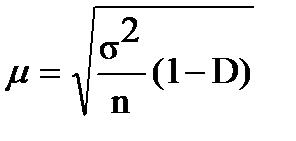 (2.5)
(2.5)
де n - обсяг вибірки,
D – частка вибіркової сукупності в генеральній
Розрахунок середньої може відбуватися за згрупованими або незгрупованими даними. У кожному випадку застосовують відповідні розрахункові формули, які необхідно навести у підрозділі.
Вказують, що для характеристики статистичного розподілу недостатньо охарактеризувати лише центр угрупування (середню величину), але необхідно знати також ступінь варіації елементів сукупності. Тому у підрозділі наводять формули розрахунків різних показників варіації (за згрупованими та незгрупованими даними), у тому числі відносних (коефіцієнтів варіації).
Окремо визначається значення для статистичного аналізу таких показників варіації, як дисперсія та середнє квадратичне відхилення, у тому числі надаються різні формули розрахунку дисперсії.
2.3 Методологія побудови та аналізу моделі парної регресії
Оскільки статистичні явища пов'язані між собою та обумовлюють одне одне, то необхідні спеціальні статистичні методи аналізу, які дозволяють вивчити форму, близькість та інші параметри статистичних взаємозв'язків. Одним з таких методів є кореляційний аналіз. На відміну від функціональних залежностей, при яких зміна будь-якої ознаки – функції – повністю та однозначно визначається зміною іншої ознаки-аргументу, при кореляційних формах зв'язку змінам одного або декількох факторів відповідає зміна середнього значення результативної ознаки. При цьому фактори, що розглядаються визначають результативну ознаку повністю.
За даними курсової роботи на рівень продуктивності праці оказують вплив не тільки показники фондомісткості, стажу та інші, але й багато інших: технічний рівень виробництва, характер організації праці і т.д. У тому випадку, якщо досліджується зв'язок між одним фактором та однією ознакою, зв'язок має назву однофакторного та кореляція є парною. Якщо досліджується зв'язок між декількома факторами та однією ознакою, зв'язок має назву багатофакторного та кореляція є множинною.
На першому етапі дослідження взаємозв'язків між факторами необхідно з множини факторів, які сформовані шляхом інтуітивних міркувань, відібрати ті, які дійсно вагомі з точки зору їхнього впливу на показник. Рішення завдань такого виду здійснюється за допомогою дисперсійного аналізу – однофакторного, якщо перевіряється істотність впливу того чи іншого фактора, або багатофакторного у випадку вивчення впливу на нього комбінації факторів.
Для вивчення зв'язку між явищами та їх ознакам будують кореляційну таблицю та аналітичне угрупування.
Кореляційна таблиця – це спеціальна комбінаційна таблиця, в якій наведено групування за двома пов'язаними ознаками: факторною та результативною. Концентрація частот біля діагоналей матриці свідчить про наявність кореляційного зв'язку між ознаками.
Аналітичне угрупування дозволяє вивчити взаємозв'язок факторної та результативної ознаки. Основні етапи проведення такого угрупування:
1. Обґрунтування факторної та результативної ознаки.
2. Підрахунок кількості одиниць в кожній з груп, що утворені.
3. Визначення обсягу ознак, що варіюють, в границях створених груп.
4. Розрахунок середніх значень результативної ознаки.
Результати групування оформлюються у таблиці (див. табл. 2.2).
Кількість груп можна визначити за формулою Стреджесса, методом «сігм» або прийняти самостійно.
Таблиця 2.3- Схема аналітичного угрупування
| Межі угрупування по факторній ознаці, хj | Кількість одиниць сукупності, fi | Середнє значення результативної ознаки у групі j, уj |
| f1 | у1 | |
| f2 | у2 | |
| :: | :: | |
| Разом |  fi fi
| х |
Відомо, що якщо сукупність розбито на групи за певною ознакою х, то для будь-якої іншої ознаки у можна обчислити середню як у цілому по сукупності, так і в кожній групі. Центром розподілу сукупності в цілому є загальна середня
 або
або  або
або  (2.6)
(2.6)
центром розподілу в j -й групі — групова середня
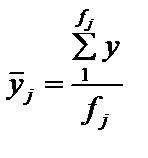 або
або  (2.7)
(2.7)
де fi – частота і-го елементу сукупності,
nj = fj - обсяг j -ї групи,
n - обсяг сукупності
Для перевірки істотності зв'язку можна використовувати характеристику F-критерій (критерій Фішера), який визначається за формулою: 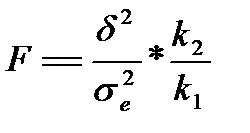 , (2.8)
, (2.8)
де 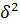 ,
, 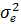 - відповідно факторна (міжгрупова) та залишкова дисперсія
- відповідно факторна (міжгрупова) та залишкова дисперсія
k1, k2 - число ступенів свободи відповідно факторної та залишкової дисперсії
 = m - 1;
= m - 1;
 = n – m (2.9)
= n – m (2.9)
де n, m - відповідно число одиниць сукупності та кількість груп.
 (2.10)
(2.10)
 (2.11)
(2.11)
Тобто
 , (2.12)
, (2.12)
де  (2.13)
(2.13)
 (2.14)
(2.14)
де уij – значення показника у, якій відповідає і -му елементу в j –й групі
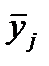 - середнє значення показника у в j –й групі
- середнє значення показника у в j –й групі
Надалі одержане розрахункове значення F порівнюється за табличним (критичним), для визначеного рівня істотності a (звичайно 0,05 або 0,01) та ступенів свободи k1 та k2.
Якщо Fрозр ≤ F табл, то вплив відповідного фактора визнається неістотним. Якщо, навпаки, Fрозр ≥ Fтабл – вплив істотний.
Сформований у результаті процедури, що описана, набір істотних факторів використовується на наступних етапах дослідження: при побудові відповідних парних моделей регресії або рівняння множинної регресії.
Надалі проведемо дослідження зв'язку між одним фактором та однією ознакою, тобто аналіз моделі парної регресії. Рівняння регресії будемо досліджувати у вигляді Y=| 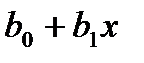 (де Y — розрахунковий (теоретичний) рівень результативної ознаки).
(де Y — розрахунковий (теоретичний) рівень результативної ознаки).
Розрахунок коефіцієнтів рівняння можна здійснити за формулами
 (2.15)
(2.15)
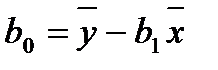
Необхідно побудувати кореляційне поле за емпіричними (вихідними) даними та «наложити» на нього лінію регресію, що побудована за визначенним рівнянням регресії, що дозволяє зробити попередні висновки про відповідність рівняння вихідним даним.
Вплив та напрямок однофакторного зв'язку характеризує лінійний коефіцієнт кореляції, який можна визначити за формулою
 (2.16)
(2.16)
Зауважимо, що за формулою лінійного коефіцієнту розраховуються також парні коефіцієнти кореляції, які характеризують тісноту зв'язку між парами змінних, що розглядаються (без урахування їх взаємодії з іншими змінними).
Показником тісноти зв'язку між результативною та факторною ознакою є коефіцієнт детермінації (множинної кореляції)
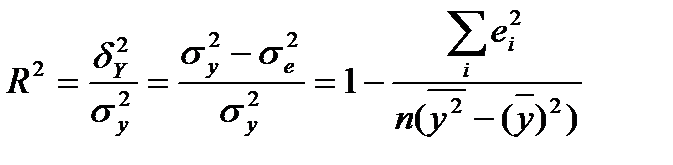 (2.17)
(2.17)
де  — загальна дисперсія ознаки y;
— загальна дисперсія ознаки y;
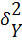 - факторна дисперсія;
- факторна дисперсія;
σ - залишкова дисперсія
 (2.18)
(2.18)
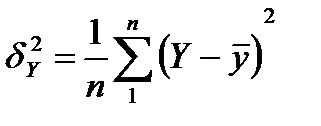 (2.19)
(2.19)
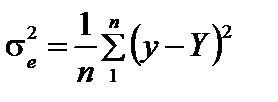 (2.20)
(2.20)
де Y, у |в| - відповідно розрахункові та фактичні значення результативної ознаки.
Тобто 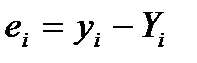 (2.21)
(2.21)
Якщо 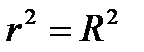 , це свідчить про лінійний зв'зок між х та у.
, це свідчить про лінійний зв'зок між х та у.
Для встановлення адекватності моделі можна також використовувати F-критерій Фішера
 (2.22)
(2.22)
Тобто у випадку парної кореляції для лінійної моделі розрахункове значення F можна знайти за формулою
 (2.23)
(2.23)
Як і в методі аналітичних групувань, надалі одержане розрахункове значення F порівнюється за табличним (критичним) для визначеного рівня істотності a (звичайно 0,05 або 0,01), тобто з Fα(1, n-2)
Якщо Fрозр ≤ F табл, то вплив відповідного фактора визнається неістотним. Якщо, навпаки, Fрозр ≥ Fтабл – вплив істотний.
Необхідно також здійснювати оцінку статистичної значущості коефіцієнтів b0 та b1. Така оцінка здійснюється за допомогою t -критерію Ст'юдента. При цьому визначають розрахункові (фактичні) значення:
- для параметру b1
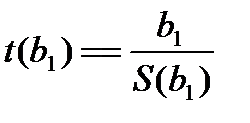 (2.24)
(2.24)
- для параметру b0
 (2.25)
(2.25)
де S(b) – середньоквадратичне відхилення відповідного параметру
 (2.26)
(2.26)
 (2.27)
(2.27)
де S2(b) – дисперсія відповідного параметру
Розрахункові значення t -критерію Ст'юдента порівнюють з табличними, які обираються в залежності від рівня істотності a та числа ступенів свободи n - m -1 (де n – обсяг вибірки, m - кількість факторних ознак, що включено до моделі, тобто для однофакторної моделі число ступенів свободи дорівнює n-2). Критичні значення можна визначити за додатком 3 (наприклад, для одностороньої критичної області t0,05;14 =1,76). Параметр визнається істотним, якщо розрахункове значення більше табличного.
За відповідними розрахунками можливо також одержати прогноз довірчого інтервалу для значення yn+1 та для його математичного очікування Myn+1.
Для значення yn+1 границі довірчих меж визначаються за формулою
 (2.28)
(2.28)
Для значення Myn+1 границі довірчих меж визначаються за формулою
 , (2.29)
, (2.29)
де S2- незсунена оцінка для залишкової вибіркової дисперсії
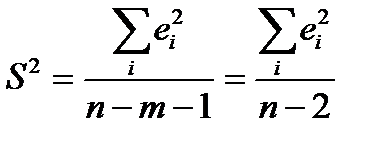 , (2.30)
, (2.30)
2.4. Методологія множинного регресійного аналізу.
Економічні явища залежать від великої кількості факторів. Тому на практиці часто використовують рівняння множинної факторів регресії, коли на величину результативної ознаки впливають два і більш фактори.
Одна з умов кореляційного аналізу - однорідність досліджуваної інформації. Критерієм однорідності інформації служать коефіцієнти варіації, які розраховуються по кожному факторному й результативному показнику.
Коефіцієнт варіації показує відносну міру відхилення окремих значень від середньоарифметичної.
Після відбору факторів і оцінки початкової інформації важливим завданням є моделювання зв'язку між факторним і результативним показником. На практиці найчастіше використовують багатофакторні лінійні моделі і моделі, які приводяться до лінійного вигляду відповідними перетвореннями, тобто
 (2.31)
(2.31)
Рішення задачі багатофакторного кореляційного аналізу передбачає визначення парних коефіцієнтів кореляції, які характеризують тісноту зв'язку між парами змінних, що розглядаються (без врахування їхньої взаємодії з іншими змінними). Парні коефіцієнти кореляції можна розрахувати за формулою лінійного коефіцієнту.
Показником тісноти зв'язку між результативною та факторними ознаками є коефіцієнт множинної кореляції. У випадку лінійного двохфакторного зв'язку він може бути розрахован за формулою
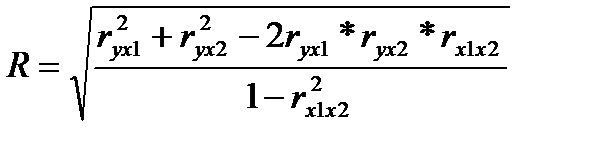 (2.32)
(2.32)
де r – лінійні (парні) коефіцієнти кореляції.
Значення цього коефіцієнту змінюється від 0 до 1. Коефіцієнт R2 має назву множинного коефіцієнту детермінації та показує, яка частка варіації результативної ознаки обумовлена впливом факторів, що враховано.
Наступним етапом кореляційно регресійного аналізу є побудова рівняння множинної регресії та визначення невідомих параметрів b0, b1,b2,….,b m обраноїх функції. Наприклад, рівняння двохфакторної лінійної регресії має вигляд  (2.33)
(2.33)
де Y - розрахункові значення результативної ознаки,
хі – значення факторних ознак,
b0, b1,b2 – параметри рівняння регресії
Для визначення параметрів 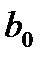 ,
,  ... необхідно скласти і вирішити систему нормальних рівнянь. При двох факторах система рівнянь набуває вигляду
... необхідно скласти і вирішити систему нормальних рівнянь. При двох факторах система рівнянь набуває вигляду
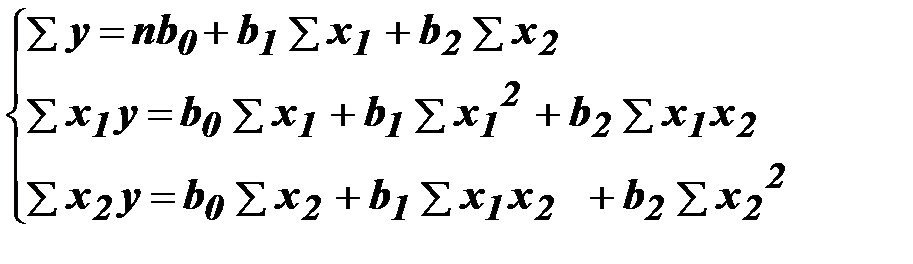 (2.34)
(2.34)
Рівняння лінійної множинної регресії можна також одержати, використовуючи програму «Microsoft Excel – Статистические функции – ЛИНЕЙН». Функція ЛИНЕЙН повертає масив { bm; bm-1;...; b1;b }, де m - кількість факторних ознак, що включено до моделі
Синтаксис функції ЛИНЕЙН
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 755; Нарушение авторских прав?; Мы поможем в написании вашей работы!