Побудова економіко-математичної моделі для однофакторного зв'язку. Перевірка якості моделі

На першому етапі вирішується питання про істотність впливу факторів, що досліджуються. Для цього необхідно побудувати кореляційні таблиці (табл. 3.5 та 3.6) відповідно за результативною та кожною з факторних ознак.

Таблиця 3.5 – Комбінаційний розподіл підприємств за рівнем витрат робочого часу та продуктивністю праці працівників

Рівень втрат робочого часу, %	Продуктивність праці, грн. / люд.-годину	Середній рівень продуктивності праці робітника, грн./люд-годину
70,1- 76,6	76,6- 83,1	83,1- 89,6	89,6- 96,1	96,1- 102,6	Разом
3,4-6,06							98,05
6,06-8,72							87,98
8,72-11,38							83,1
11,38-14,04							87,65
14,04-16,7							74,98
По сукупнос­ті в цілому							85,27

Для розрахунку 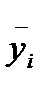скористаймося формулою 2.24, тоді:

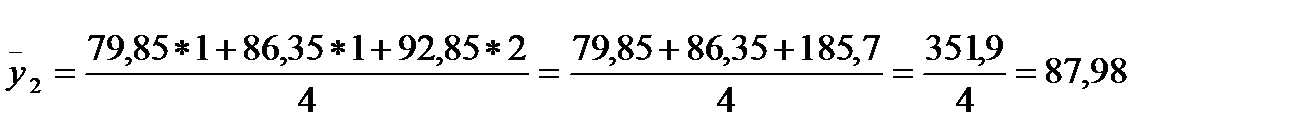
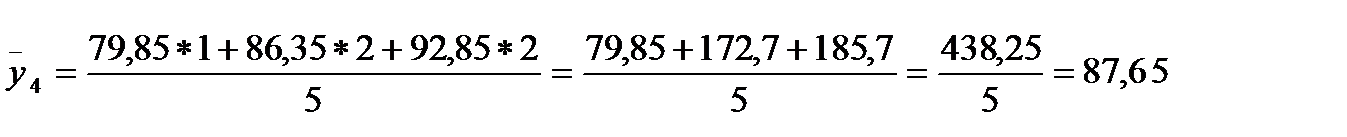
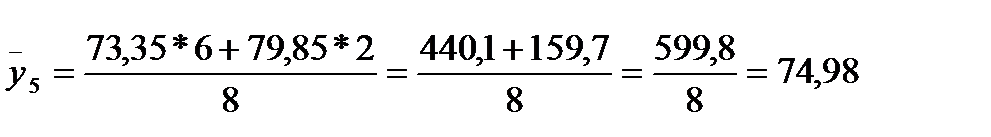
Для розрахунку скористаймося формулою 2.25, тоді:

Таблиця 3.6 – Комбінаційний розподіл підприємств за стажем та продуктивністю праці працівників

Стаж років	Продуктивність праці, грн. / люд.-годину	Середній рівень продуктивності праці робітника, грн./люд-годину
70,1- 76,6	76,6- 83,1	83,1- 89,6	89,6- 96,1	96,1- 102,6	Разом
8,4- 10,22							78,67
10,22-12,04							87,98
12,04-13,86							86,35
13,86-15,68							96,1
15,68-17,5							94,48
По сукупнос­ті в цілому							85,27

Для розрахунку 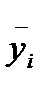скористаймося формулою 2.24, тоді:

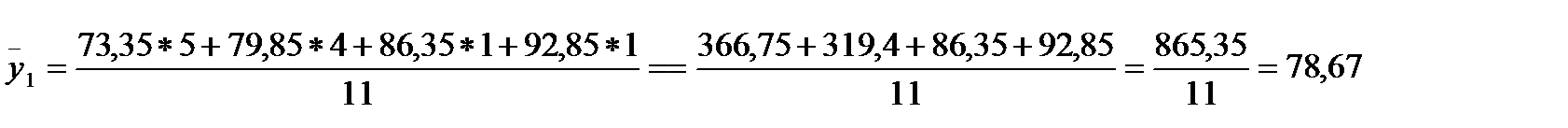
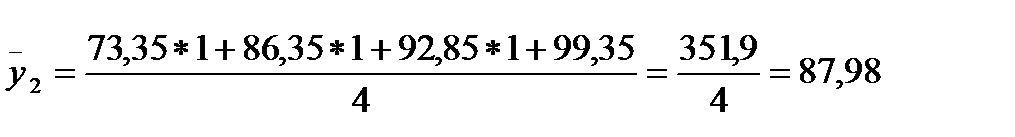
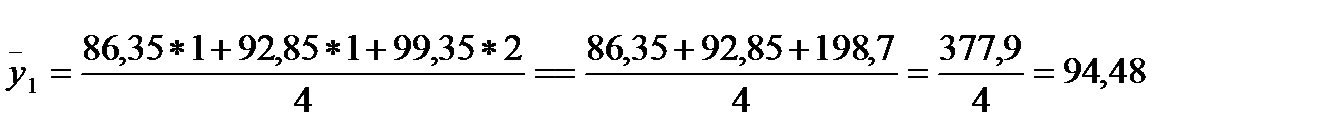
Для розрахунку скористаймося формулою 2.25, тоді:

Визначення істотності впливу рівня втрат робочого часу на продуктивність праці

За вихідними даними показник рівень втрат робочого часу має мінімальне значення 3,4, максимальне 16,7. Розподілимо значення на групи, визначив n =5. У цьому випадку ширина інтервалу становить (16,7– 3,4): 5 = 2,66. Побудуємо розрахункову таблицю для відбору факторів, що впливають на вихідний показник.

Таблиця 3.7 – Розрахунки для обґрунтування відбору факторів, що впливають на вихідний показник

Номер групи	Значення границь груп за фактором х	Кількість елементів у групі (частота)	Значення показника у, що відповідають елементам групи	Групові середні
	3,4-6,06		96,9; 91,5; 96,9; 100,4; 102,6	97,66
	6,07-8,73		80,2; 91,2; 90; 84,8	86,55
	8,74-11,4		82,2; 83,6	82,9
	11,41-14,07		79,7; 90; 87,8; 85,1; 91,8	86,88
	14,08-16,74		74,3; 70,1; 79,6; 75,5; 70,8; 74,6; 82,6; 74,8	75,29

Розрахуємо за формулою (2.7) групові середні та занесемо їх у графу 5

таблиці 3.7.

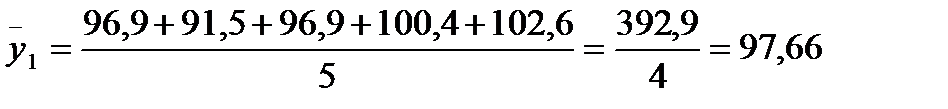
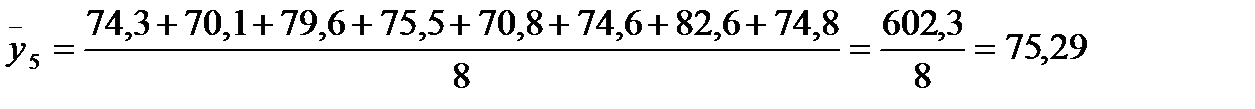
Розрахуємо загальну середню за формулою (2.6)

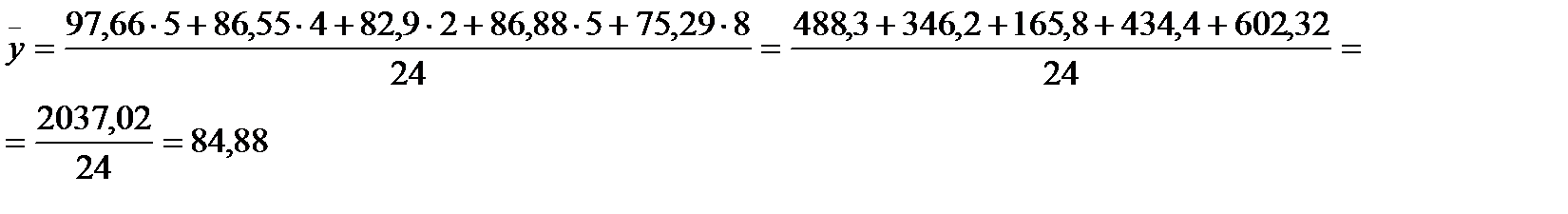Надамо розрахунки до міжгрупової варіації (дисперсії). Допоміжні розрахунки наведено у таблиці 3.8.

Таблиця 3.8. – Розрахунок до міжгрупової дисперсії

Групові середні,
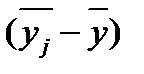
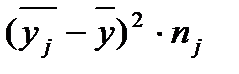
97,66	12,78	163,33	816,64
86,55	1,67	2,79	11,16
82,9	-1,98	3,92	7,84
86,88		4,00	20,00
75,29	-9,59	91,97	735,74
Усього			1591,38

Тобто Q₁= 1591,38.

Залишкова варіація характеризується величиною Q₂, яка розраховується наступним чином:

Q2=(96,9-97,66)²+(91,5-97,66)²+(96,9-97,66)²+(100,4-97,66)²+(102,6-97,66)²++(80,2-86,55)²+(91,2-86,55)²+(90-86,55)²+(84,8-86,55)²+ (82,2-82,9)²+(83,6-82,9)²+(79,7 -86,88)²+(90-86,88)²+(87,8-86,88)²+ (85,1—86,88)²++ (91,8-86,88)²+(74,3-75,29)²+(70,1-75,29)²+(79,6-75,29)²+(75,5-75,29)²+(70,8-75,29)²+(74,6-75,29)²+(82,6-75,29)²+(74,8-75,29)²=0,58+37,95+0,58+7,51 +24,4++40,32+21,62+11,9+3,06+0,49+0,49+51,55+9,73+0,85+3,17+24,21+0,98++26,94+18,58+0,04+20,16+0,48+53,44+0,24=359,27

Тоді

Ϝ=

Табличне значення критерію Фішеру дорівнює F_0,05 (4;19)=2,87, тобто розрахункове значення перевищує критичне, відповідно вплив фактора на вихідний показник визнається істотним.

Визначення істотності впливу рівня стажу на продуктивність праці

За вихідними даними показник стаж років мінімальне значення 8,4, максимальне 17,5. Розподілимо значення на групи, визначив n =5. У цьому випадку ширина інтервалу становить (17,5–8,4):5=1,82. Побудуємо розрахункову таблицю для відбору факторів, що впливають на вихідний показник.

Таблиця 3.9 – Розрахунки для обґрунтування відбору факторів, що впливають на вихідний показник

Номер групи	Значення границь груп за фактором х	Кількість елементів у групі (частота)	Значення показника у, що відповідають елементам групи	Групові середні
	8,4-10,22		74,3; 70,1; 79,6; 75,5; 70,8; 79,7; 74,6; 82,9; 90; 87,8; 80,2	78,68
	10,23-12,05		74,8; 85,1; 90; 96,9	86,7
	12,06-13,88		82,2; 83,6; 91,2	85,7
	13,89-15,71		91,8; 100,4	96,1
	15,72-17,54		84,8; 91,5; 96,9; 102,6	93,95

Розрахуємо за формулою (2.7) групові середні та занесемо їх у графу 5

таблиці 3.9.

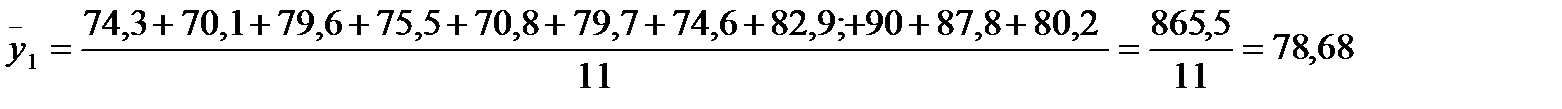
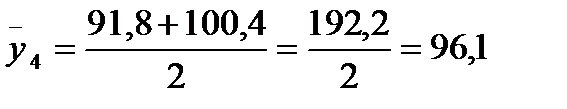
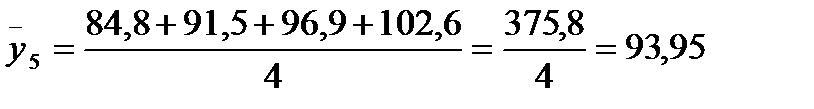
Розрахуємо загальну середню за формулою (2.6)

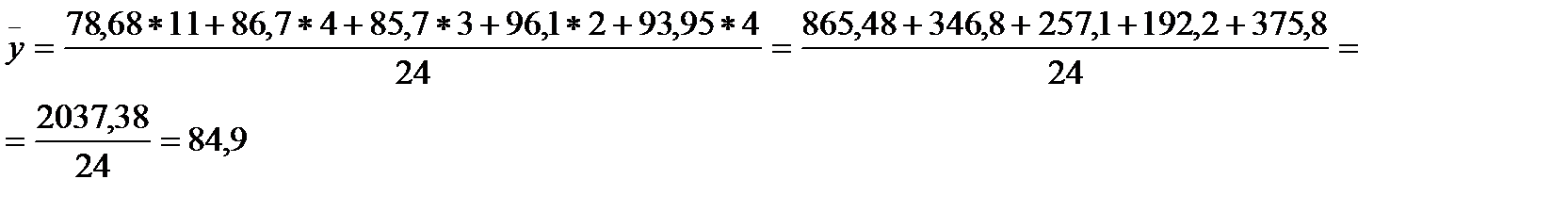
Надамо розрахунки до міжгрупової варіації (дисперсії) (табл.. 3.10).

Таблиця 3.10. – Розрахунок до міжгрупової дисперсії

Групові середні,
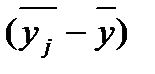
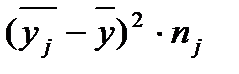
78,68	-6,22	38,69	425,57
86,7	1,8	3,24	12,96
85,7	0,8	0,64	1,92
96,1	11,2	125,44	250,88
93,95	9,05	81,90	327,61
Усього			1018,94

Тобто Q₂= 1018,94.

Залишкова варіація характеризується величиною Q₂, яка розраховується наступним чином:

Q2=(74,3-78,68)²+(70,1-78,68)²+(79,6-78,68)²+(75,5-78,68)²+(70,8-78,68)²+ +(79,7-78,68)²+(74,6-78,68)²+(82,2-78,68)²+(90-78,68)²+(87,8-78,68)²+ +(80,2-78,68)²+(74,8-86,7)²+(85,1-86,7)²+(90-86,7)²+(96,9-86,7)²+ (82,2-85,7)²+(83,6-85,7)²+(91,2-85,7)²+(91,8-96,1)²+ (100,4-96,1)²+(84,8-93,95)²+(91,5-93,95)²+(96,9-93,95)²+(102,6-93,95)²= 19,18+73,62+0,85+10,11 +62,09+1,04+16,65+12,39+11,32+83,17+2,31+141,61+2,56+10,89+104,04+12,25+4,41+30,25+18,49+18,49+83,72+6,00+8,7+74,82=808,96

Тоді

Ϝ=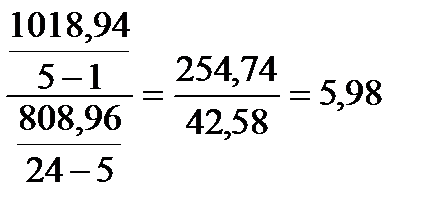

Табличне значення критерію Фішеру дорівнює F_0,05 (4;19)=2,87, тобто розрахункове значення перевищує критичне, відповідно вплив фактора на вихідний показник визнається істотним.

Надалі проведено дослідження однофакторного зв'язку між рівнем втрат робочого часу та продуктивності праці. Рівняння регресії досліджується у вигляді Y=| (де Y — розрахунковий (теоретичний) рівень результативної ознаки). На рисунку 3.7 представлено кореляційне поле за вихідними даними.

Визначення коефіцієнтів рівняння здійснилось за формулами 2.15-2.16, розрахунки представлені в таблиці 3.11 Y= b₀+b₁x

Для знаходження b₀ та b₁ скористаймося формулами 2.15:

b₁ =

b₀ = 84,89-(-1,74*10,62)=84,89+18,48=103,37

Y= 103,37-1,74х

Таблиця 3.11 – Розрахункова таблиця для визначення параметрів одно факторного зв’язку та їхньої оцінки

№ з/п							ei= =yi-Yi
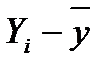
	15,4	74,3	237,16	5520,49	1144,22	76,574	-2,27	5,17	-8,316	69,15586
	16,7	70,1	278,89	4914,01	1170,67	74,312	-4,21	17,74	-10,578	111,8941
	15,9	79,6	252,81	6336,16	1265,64	75,704	3,90	15,18	-9,186	84,3826
	14,1	75,5	198,81	5700,25	1064,55	78,836	-3,34	11,13	-6,054	36,65092
	14,3	70,8	204,49	5012,64	1012,44	78,488	-7,69	59,11	-6,402	40,9856
	12,6	79,7	158,76	6352,09	1004,22	81,446	-1,75	3,05	-3,444	11,86114
	15,8	74,6	249,64	5565,16	1178,68	75,878	-1,28	1,63	-9,012	81,21614
	14,9	82,9	222,01	6872,41	1235,21	77,444	5,46	29,77	-7,446	55,44292
			144,00	8100,00	1080,00	82,49	7,51	56,40	-2,4	5,76
	14,2	74,8	201,64	5595,04	1062,16	78,662	-3,86	14,92	-6,228	38,78798
	13,2	87,8	174,24	7708,84	1158,96	80,402	7,40	54,73	-4,488	20,14214
	12,8	85,1	163,84	7242,01	1089,28	81,098	4,00	16,02	-3,792	14,37926
	11,3	82,2	127,69	6756,84	928,86	83,708	-1,51	2,27	-1,182	1,397124
	11,8	91,8	139,24	8427,24	1083,24	82,838	8,96	80,32	-2,052	4,210704
	10,7	83,6	114,49	6988,96	894,52	84,752	-1,15	1,33	-0,138	0,019044
	8,7	80,2	75,69	6432,04	697,74	88,232	-8,03	64,51	3,342	11,16896
	7,1	91,2	50,41	8317,44	647,52	91,016	0,18	0,03	6,126	37,52788
	6,5		42,25	8100,00	585,00	92,06	-2,06	4,24	7,17	51,4089
	6,1	84,8	37,21	7191,04	517,28	92,756	-7,96	63,30	7,866	61,87396
	5,2	96,9	27,04	9389,61	503,88	94,322	2,58	6,65	9,432	88,96262
	4,3	91,5	18,49	8372,25	393,45	95,888	-4,39	19,25	10,998	120,956
	4,4	96,9	19,36	9389,61	426,36	95,714	1,19	1,41	10,824	117,159
	3,4	100,4	11,56	10080,16	341,36	97,454	2,95	8,68	12,564	157,8541
	3,5	102,6	12,25	10526,76	359,10	97,28	5,32	28,30	12,39	153,5121
	254,9	2037,3	3161,97	174891,05	20844,34	2037,354	-0,05	565,13	-0,006	1376,709
	10,62	84,89	131,75	7287,13	868,51	84,89	-0,002	23,55	0,0004	57,363

r = зворотній сильний зв'язок

r² =0,71

Рисунок 3.7 – Кореляційне поле

Для знаходження коефіцієнту детермінації скористаймося формулою 2.17:

Якщо 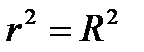, це свідчить про лінійний зв'язок між рівнем втрат робочого часу та продуктивністю праці.

Для встановлення адекватності моделі скористаймося F-критерієм Фішера за формулою 2.23:

Якщо F_розр ≥ F_табл то вплив рівня втрат робочого часу на продуктивність праці є істотним.

Оцінка статистичної значущості коефіцієнтів b₀ та b₁. Така оцінка здійснюється за допомогою t -критерію Ст'юдента. При цьому визначають розрахункові (фактичні) значення для рівня втрат робочого часу:

Оцінка для параметру b₁ визначається за формулою 2.24, для параметру b₂ за формулою 2.25. При цьому попередньо за формулами 2.26 та 2.27 визначаються

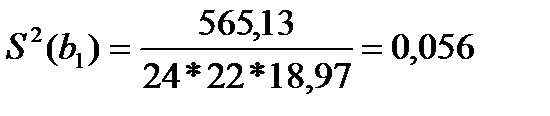
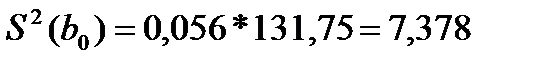
Тоді

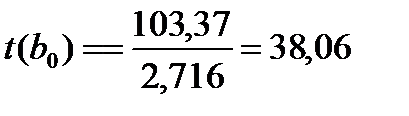
Розрахункові значення t-критерію Ст'юдента більше табличних для одностороньої критичної області t_0,05;22=1,72, одже параметри визначаються істотними.

На останньому етапі аналізу однофакторної регресії розробимо прогноз довірчого інтервалу для значення y_n+1 та для його математичного очікування My_n+1 за формулами 2.28 - 2.30. При цьому слід виконати розрахунки двох прогнозів. У першому випадку покладемо 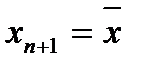, тобто прогнозне значення фактора прийнято на середньому рівні поточного року, у другому випадку розрахунок прогнозу здійснити за умови зростання середньої величини факторної ознаки на 15%, тобто

Щоб дізнатися незсунену оцінку для залишкової вибіркової дисперсії підставимо дані у формулу 2.30: ,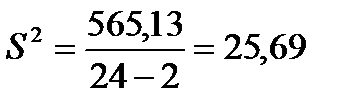

Для значення y₂₅ границі довірчих меж дорівнюють

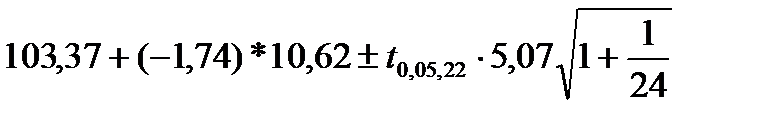
Таким чином, значення y₂₅ будуть не менше 75,999 грн./людино-годину, та не більше 93,783 грн./людино-годину.

Для значення My₂₅ границі довірчих меж дорівнюють

,

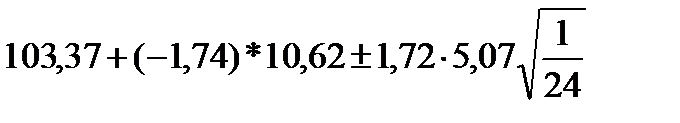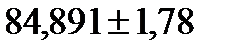
Таким чином значення My₂₅ будуть не менше 83,111 грн./людино-годину та не більше 86,671 грн./людино-годину.

У другому випадку, коли здійснюється зростання середньої величини факторної ознаки на 15%, тобто , значення y₂₅ границі довірчих меж дорівнюють

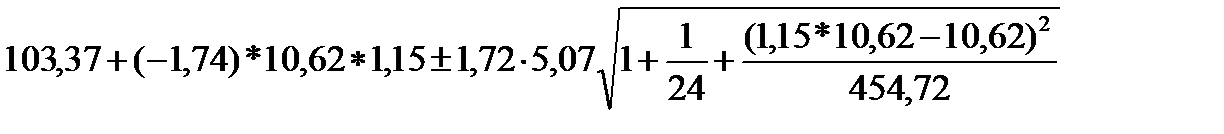
Тобто, значення y₂₅ будуть не менше 73,19 грн./людино-годину, та не більше 91,05 грн./людино-годину.

Для значення My₂₅ границі довірчих меж дорівнюють

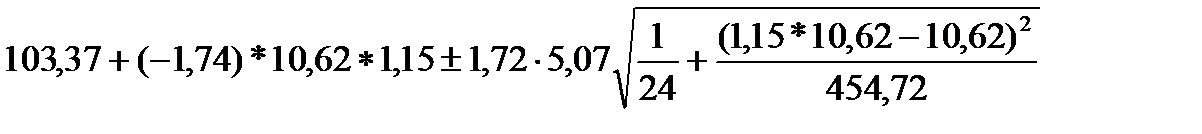
Таким чином значення My₂₅ будуть не менше 80,21 грн./людино-годину та не більше 84,03 грн./людино-годину.

3.3 Побудова та аналіз моделі багатофакторного зв'язку

Треба здійснити моделювання зв'язку між факторними|факторами| і результативним показником, використовуючи багатофакторну лінійну модель вигляду:

Так, як =0,81>0,7, то зв’язок між рівнем втрат робочого часу та стажем роботи сильний.

Множинний коефіцієнт детермінації буде дорівнюватися

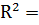0,72

Наступним етапом кореляційно регресійного аналізу є побудова рівняння множинної регресії та визначення невідомих параметрів b₀, b₁,b₂,….,b_m обраної функції. Рівняння двохфакторної лінійної регресії має вигляд

де Y - розрахункові значення результативної ознаки,

х_і – значення факторних ознак,

b₀, b₁,b₂ – параметри рівняння регресії

Для визначення параметрів 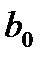, ... необхідно скласти і вирішити систему нормальних рівнянь:

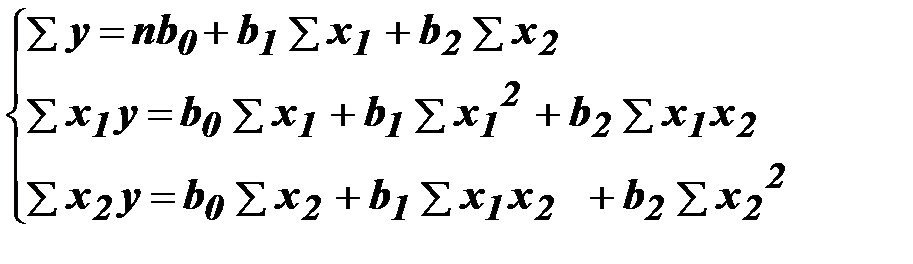
Але цей етап можна виконати використовуючи програму «Microsoft Excel – Статистическиефункции – ЛИНЕЙН». Вихідні дані набрані у програмі представлені в табл. 3.12.

Таблиця 3.12 – Вихідні дані

	Х1	Х2	У
	15,4	8,9	74,3
	16,7		70,1
	15,9	9,9	79,6
	14,1	8,9	75,5
	14,3	8,4	70,8
	12,6	10,1	79,7
	15,8	9,9	74,6
	14,9	9,7	82,9
		8,7
	14,2	10,8	74,8
	13,2	9,9	87,8
	12,8	10,5	85,1
	11,3	12,3	82,2
	11,8	13,9	91,8
	10,7	12,9	83,6
	8,7	9,8	80,2
	7,1	12,7	91,2
	6,5	10,9
	6,1	15,8	84,8
	5,2	11,4	96,9
	4,3	17,2	91,5
	4,4	17,5	96,9
	3,4	14,7	100,4
	3,5	17,4	102,6

Після того як вибрали функцію ЛИНЕЙН, у рядку формул з’явився такий запис: ЛИНЕЙН(С2:С25;A2:B25;ИСТИНА, ИСТИНА). При вводі у вигляді масиву приведена вище формула повертає результат по формі табл. 3.13.

Таблиця 3.13 – Додаткова регресійна статистика

0,354316	-1,55773	97,28051	#Н/Д	#Н/Д
0,621832	0,407787	11,12689	#Н/Д	#Н/Д
0,71457	5,147892	#Н/Д	#Н/Д	#Н/Д
26,28657		#Н/Д	#Н/Д	#Н/Д
1393,23	556,5166	#Н/Д	#Н/Д	#Н/Д

Використовуючи одержані дані можна записати рівняння множинної регресії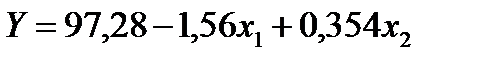

Наступним етапом є розрахунок та перевірка статистичної значущості коефіцієнту детермінації, що відповідає визначенному теоретичному рівнянню, та значущості коефіцієнтів регресії.

Коефіцієнт детермінації, який надає оцінку загальної якості моделі, визначаэться за формулою 2.35 на основі розрахунків, які провелися у табл. 3.14.

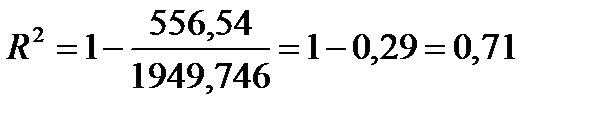
Розраховане значення коефіцієнту =0,71 дорівнює одержаному завдяки використанню програми «Microsoft Excel – Статистические функции – ЛИНЕЙН» (додаткова регресійна статистика), який дорівнює теж 0,71457.

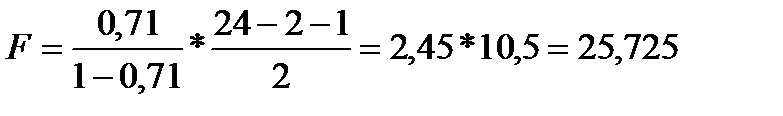
Одержане розрахункове значення F=42,525 більше табличного для рівня істотності a=0,05, тобто з F_0,05 (2; 21)=3,49. Так як F_розр > F_табл, то вплив рівня втрат робочого часу та стажу роботи на продуктивність праці визначається істотним та коефіцієнт детермінації статистично значущ.

Таблиця 3.14 – Розрахункова таблиця для визначення параметрів багатофакторного зв’язку та їхньої оцінки

№ з/п
	74,3	15,4	8,9	76,41	-2,11	4,44	-10,59	112,1481
	70,1	16,7		74,41	-4,31	18,61	-14,79	218,7441
	79,6	15,9	9,9	75,98	3,62	13,10	-5,29	27,9841
	75,5	14,1	8,9	78,43	-2,93	8,61	-9,39	88,1721
	70,8	14,3	8,4	77,95	-7,15	51,06	-14,09	198,5281
	79,7	12,6	10,1	81,20	-1,50	2,25	-5,19	26,9361
	74,6	15,8	9,9	76,14	-1,54	2,36	-10,29	105,8841
	82,9	14,9	9,7	77,47	5,43	29,49	-1,99	3,9601
			8,7	81,64	8,36	69,89	5,11	26,1121
	74,8	14,2	10,8	78,95	-4,15	17,23	-10,09	101,8081
	87,8	13,2	9,9	80,19	7,61	57,87	2,91	8,4681
	85,1	12,8	10,5	81,03	4,07	16,57	0,21	0,0441
	82,2	11,3	12,3	84,01	-1,81	3,26	-2,69	7,2361
	91,8	11,8	13,9	83,79	8,01	64,12	6,91	47,7481
	83,6	10,7	12,9	85,15	-1,55	2,42	-1,29	1,6641
	80,2	8,7	9,8	87,18	-6,98	48,68	-4,69	21,9961
	91,2	7,1	12,7	90,70	0,50	0,25	6,31	39,8161
		6,5	10,9	91,00	-1,00	1,00	5,11	26,1121
	84,8	6,1	15,8	93,36	-8,56	73,23	-0,09	0,0081
	96,9	5,2	11,4	93,20	3,70	13,66	12,01	144,2401
	91,5	4,3	17,2	96,66	-5,16	26,63	6,61	43,6921
	96,9	4,4	17,5	96,61	0,29	0,08	12,01	144,2401
	100,4	3,4	14,7	97,18	3,22	10,37	15,51	240,5601
	102,6	3,5	17,4	97,98	4,62	21,35	17,71	313,6441
Ʃ	2037,3	254,9	281,2	2036,62		556,54		1949,746
1/nƩ	84,89	10,62	11,72	84,86

Оцінка істотності коефіцієнтів регресії здійснюється за допомогою t-критерію Ст'юдента. При цьому визначають розрахункові (фактичні) значення t-критерію за формулою 2.37 на основі даних, одержаних за допомогою програми «Microsoft Excel – Статистические функции – ЛИНЕЙН» (додаткова регресійна статистика) (див. табл. 3.13).

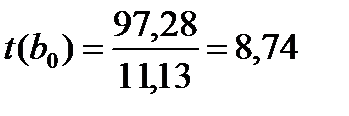
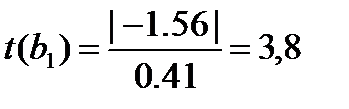
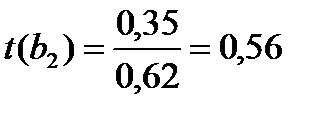
Розрахункові значення t-критерію Ст'юдента для параметрів b0 та b1 більше табличного, який дорівнює t_0,05;21=1,72, таким чином ці параметри рівняння визначаються істотними.. t(b₂) =0.56, цей параметр рівняння не є істотними.

Висновки по розділу 3

На основі вихідних незгрупованих даних визначено середні величини, які для продуктивності праці дорівнює 84,89 грн./люд.-годину, рівня втрат робочого часу 10,62%, а для стажу роботи 11,72 рр. Дисперсія дорівнює 80,82; 18,97; 8,07 відповідно. Проаналізувавши коефіцієнти варіації можна зробити висновок, що сукупність є однорідною по всім ознакам. У генеральній сукупності в 95,4 випадках із 100 ми можемо стверджувати, що середня продуктивність праці не менше 81,15 грн./люд.-годину та не більше 88,63 грн./люд.-годину; середній рівень втрат робочого часу не менше 8,8% та не більше 12,44%; середній стаж роботи не менше 10,54 років та не більше 12,9 років.

Проведена перевірка істотності зв'язку для кожної ознаки, використовуючи F-критерій Фішера, так як розрахункові значення більше табличного, то виплив факторних ознак на результативною визначається істотним. Знайдені коефіцієнти рівняння регресії та проведен аналіз статистичної значущості цих коефіцієнтів. Між продуктивністю праці та рівнем втрат робочого часу є кореляційний зв'язок. Так як частоти розташовані по діагоналі з нижнього кутка справо на ліво, то зв'язок зворотній. Між продуктивністю праці та стажем роботи також спостерігається кореляційний зв'язок. Так як частоти розташовані по діагоналі з верхнього кутка зліва праворуч, то зв'язок прямий.

Побудована статистико-економічна модель багатофакторного зв’язку між продуктивністю праці та рівнем втрат робочого часу, стажу роботи. Визначення параметрів рівняння регресії відбулося за допомогою програми «Microsoft Excel – Статистические функции – ЛИНЕЙН». Розрахований коефіцієнт детермінації дорівнюється коефіцієнту детермінації, який знайден за допомогою програми. Перевірена статистична істотність коефіцієнту детермінації за допомогою критерію Фішера. За допомогою t-критерію Ст'юдента визначена істотність параметрів рівняння регресії.

ВИСНОВКИ

1. В результаті виконання курсової роботи були досліджені важливіші статистичні характеристики, їх сутність та умови використання; методи розрахунку та аналізу статистичних показників; методи встановлення та аналізу взаємозв'язків соціально-економічних явищ; методи та прийоми економіко-статистичного аналізу розвитку виробництва.

2. В результаті виконання курсової роботи були проведені розрахунки показників статистичних рядів та рядів розподілу; проводились математико-статистичний і економіко-статистичний аналіз результатів спостережень та були розраховані узагальнюючі техніко-економічні показники роботи підприємств; проведений обґрунтований аналіз взаємозв'язків між показниками, самостійного творчого мислення; кількісної оцінки та якісної характеристики стану підприємства; проведення аналізу взаємозв'язків показників діяльності підприємства; розрахунків узагальнюючих показників роботи підприємства та аналізу показників статистичних рядів та рядів розподілу з метою використання їх для прогнозування показників діяльності підприємств.

3. У третьому розділі роботи за вихідними даними були побудовані угрупування за результативною та кожною факторною ознакою. Ряди розподілу представлені графічно у вигляді полігону та гістограми. Між продуктивністю праці та рівнем втрат робочого часу є кореляційний зв'язок. Так як частоти розташовані по діагоналі з нижнього кутка справо на ліво, то зв'язок зворотній. Між продуктивністю праці та стажем роботи також спостерігається кореляційний зв'язок. Проведена перевірка істотності зв'язку для кожної ознаки, використовуючи F-критерій Фішера, так як розрахункові значення більше табличного, то виплив факторних ознак на результативною визначається істотним. Знайдені коефіцієнти рівняння регресії та проведен аналіз статистичної значущості цих коефіцієнтів.

ПЕРЕЛІК ПОСИЛАНЬ

1.. Статистика: Курс лекцій (для студентів денної та заочної форм навчання напрямів підготовки 6.030504 „Економіка підприємства” та 6.030507 „Маркетинг” галузі знань 0305 „Економіка та підприємництво”) / Уклад.: Мізіна О.В. – Донецьк: ДонНТУ, 2009. - 134 с.

2. Методичні рекомендації щодо виконання завдань практичних занять з нормативної навчальної дисципліни циклу природничо-наукової та загальноекономічної підготовки «Статистика» для студентів денної (заочної, денно-заочної) форми навчання галузі знань: 0305 «Економіка та підприємництво», напрями підготовки: 6.030504 «Економіка підприємства», 6.030507 «Маркетинг» / Укл.: О.В. Мізіна, Г.А. Какуніна. - Донецьк: ДоНТУ, 2010. – 111 с.

3. Харченко Л.П., Долженкова В.Г. і др. Статистика: курс лекцій. Москва, 2000. 310 с.

4. Статистика: Підручник / С. С. Герасименко, А. В. Головач, А. М. Єріна та ін.; За наук. ред. д-ра екон. наук С. С. Герасименка. — 2-ге вид., перероб. і доп. — К.: КНЕУ, 2000. — 467 с.

5. Статистика: Підручник/ А.В. Головач, А.М. Єріна та ін.; 3а ред. А.В.Головача. - К.: Вища шк., 1993. - 623 с.

6. Статистика: Підручник / С. С. Герасименко та ін. — К.: КНЕУ, 1998. — 468 с.

7. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 7-е, стер. - М.: Высш. школа, 2000. - 479 с.

Дата добавления: 2014-12-24