В партии из 7 деталей имеется пять деталей первого сорта. Наудачу отобраны 4 детали для проверки. Найти закон распределения числа деталей первого сорта среди отобранных. 1 страница

Сигнализатор снабжен 3 независимо работающими элементами. Вероятность того, что при аварии сработает 1-ый элемент, равна 0,4, для остальных эти вероятности соответственно равны 0,6 и 0,75. Найти закон распределения числа сработавших элементов.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	1	2	-1	3
Y	2	3	1	4

Предполагая, что между X и Y имеется зависимость вида 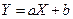найти неизвестные коэффициенты a и b по методу наименьших квадратов. Вычислить Y при .

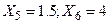10. По схеме собственно-случайной бесповторной выборки проведено 10%-ное обследование предприятий одной из отраслей экономики в отчетном году. Результаты обследования представлены в таблице:

Выпуск продукции, млн.руб.	Менее 30	30– –40	40– –50	50– –60	60– –70	70– –80	80– –90	Более 90	Итого:
Число предприятий

Используя -критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X –объем выпуска продукции – распределена равномерно.

Вариант №6

1. В группе 14 человек, 4 из которых неуспевающих. По списку вызывают сразу пять человек. Найти вероятность того, что два из них будут неуспевающими.

2. Вероятности выполнить норму для каждого из трех спортсменов соответственно равны 0,7; 0,8 и 0,9. Найти вероятность того, что ее выполнят хотя бы один из них.

3. Вероятности поймать карпа у трех рыбаков равны: 0,5, 0,7, 0,95. Найти вероятность того, что поймал карпа только один рыбак.

4. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго – 0,9. Найти вероятность того, что взятая наудачу из наудачу взятого набора деталь стандартная.

5. Вероятность выиграть в студенческой новогодней лотерее равна 0,3. Найти вероятность того, что среди 30 купленных студентом билетов окажется 10 выигрышных.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,3, математическое ожидание М(Х) = 3,7 и дисперсия D(X) = 0,21. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), D(X), если задан ряд распределения случайной величины Х:

Х
Р(Х)	0,28	0,12	0,45	??

8. Производится ряд выстрелов по мишени с вероятностью попадания 0,6 при каждом. Стрельба ведётся до первого попадания в мишень, но не более четырёх выстрелов. Найти закон распределения числа произведённых выстрелов.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	1	2	4	6
Y	2	2,5	2,3	2,1

Предполагая, что между X и Y имеется зависимость вида 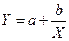найти неизвестные коэффициенты a и b по методу наименьших квадратов. Вычислить Y при .

10. Распределение 50 российских коммерческих банков по объему вложений в ценные бумаги X (тыс. руб.) и полученной прибыли Y (тыс. руб.) представлены в таблице:

Y x	100–120	120–140	140–160	160–180	180–200	200–220	Итого:
1000–1300
1300–1600
1600–1900
1900–2200
2200–2500
Итого:

Необходимо: вычислить коэффициент корреляции и сделать вывод о тесноте и направлении связи между переменными X и Y.

Вариант №7

1. В урне 3 белых и 8 черных шаров. Из урны вынимают сразу шесть шаров. Найти вероятность того, что три из них будут белыми.

2. Вероятности землетрясения в каждом из трех городов соответственно равны 0,2; 0,8 и 0,6. Найти вероятность того, что землетрясение произойдет только в двух городах.

3. Три стрелка произвели залп по цели. Вероятности поражения цели каждым стрелком соответственно равны 0,8, 0,9, 0,6. Найти вероятность того, что хотя бы один стрелок поразит цель.

4. На предприятии работают две бригады рабочих: первая производит ¾ продукции с процентом брака 5%, вторая - ¼ продукции с процентом брака 2%. Найти вероятность того, что наугад взятое не-бракованное изделие изготовлено второй бригадой.

5. Институт выпускает 80% специалистов высокого класса. Найти вероятность того, что среди 5000 выпущенных специалистов окажется 3700 высокого класса

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,9, математическое ожидание М(Х) = 2,2 и дисперсия D(X) = 0,36. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), D(X), если задан ряд распределения случайной величины Х:

Х
Р(Х)	??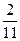

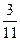
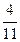
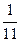
8. Вероятность попадания в цель из орудия при первом выстреле равна 0,7, при втором – 0,3, при третьем – 0,5. Найти закон распределения числа попаданий в цель, если произведено три выстрела.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	-1	0	1	4
Y	0	1	2	5

Предполагая, что между X и Y имеется зависимость вида 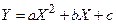найти неизвестные коэффициенты a, b и c по методу наименьших квадратов. Вычислить Y при .

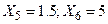10. Данные об урожайности зерновых культур в некотором регионе получены с помощью собственно-случайной бесповторной выборки. Результаты обследования 100 предприятий из 1000 приведены в таблице:

Урожайность, ц/га	20– –30	30– –40	40– –50	50– –60	60– –70	70– –80	80– –90	90– –100	Итого:
Число предприятий

Используя -критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X – урожайность зерновых культур – распределена равномерно.

Вариант №8

1. В ящике 15 деталей, 9 из которых стандартных. Из ящика вынимают сразу шесть деталей. Найти вероятность того, что три из них будут стандартными.

2. Вероятности попадания в цель для каждого из трех орудий соответственно равны 0,9; 0,8 и 0,55. Найти вероятность того, что попадет в цель хотя бы одно орудие.

3. Чему равна вероятность того, что при бросании трех игральных костей хотя бы на двух из них появится 6 очков?

4. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы 5, из второй 6, из третьей – 10 студентов. Вероятность того, что студент первой, второй и третьей группы попадают в сборную института, соответственно равны 0,9, 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования не попал в сборную. Найти вероятность того, что студент из первой группы.

5. Вероятность того, что расход электроэнергии за одни сутки не превысит нормы, равна 0,8. Найти вероятность того, что в ближайшие 10 суток расход электроэнергии в течение хотя бы 4 суток не превысит нормы.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,9, математическое ожидание М(Х) = 3,1 и дисперсия D(X) = 0,09. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), D(X), если задан ряд распределения случайной величины Х:

Х
Р(Х)	0,25	0,05	??	0,3

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	0	1	5	6
Y	5	3	4	7

Предполагая, что между X и Y имеется зависимость вида 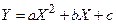найти неизвестные коэффициенты a, b и c по методу наименьших квадратов. Вычислить Y при .

10. Распределение 80 литейных цехов машиностроительных заводов по степени компьютеризации процессов производства X (%) и производственным затратам Y (млн. руб.) представлено в таблице:

y x	5–6	6–7	7–8	8–9	9–10	Итого:
10–20
20–30
30–40
40–50
50–60
60–70
Итого:

Необходимо: вычислить коэффициент корреляции и сделать вывод о тесноте и направлении связи между переменными X и Y.

Вариант №9

1. В урне 4 белых и 7 черных шаров. Из урны вынимают сразу пять шаров. Найти вероятность того, что два из них будут белыми.

2. Вероятности землетрясения в каждом из трех городов соответственно равны 0,1; 0,8 и 0,6. Найти вероятность того, что землетрясение произойдет только в одном городе.

3. В типографии имеется 10 плоскопечатных машин. Для каждой машины вероятность того, что она работает в данный момент, равна 0,85.Найти вероятность того, что в данный момент работают только три машины.

4. В группе спортсменов 10 лыжников, 7 велосипедистов и 8 бегунов. Вероятности выполнить квалификационную норму соответственно равны 0,6, 0,8, 0,9. Наудачу выбранный спортсмен выполнил норму. Найти вероятность того, что это лыжник.

5. Вероятность поражения мишени стрелком при одном выстреле 0,7. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень не менее 6 раз.

6.. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,1, математическое ожидание М(Х) = 3,9 и дисперсия D(X) = 0,09. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), s(Х), если задан ряд распределения случайной величины Х:

Х
Р(Х)	0,4	0,25	0,25	0,1

8. Испытуемый прибор состоит из трёх малонадёжных элементов. Отказы элементов независимы, а их вероятности равны соответственно 0,05; 0,2; 0,1. Найти закон распределения числа отказавших за время Т элементов.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	1	2	-1	3
Y	2	3	1	4

Предполагая, что между X и Y имеется зависимость вида 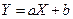найти неизвестные коэффициенты a и b по методу наименьших квадратов. Вычислить Y при .

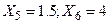10. В результате выборочного обследования 100 предприятий из 1000 по схеме собственно-случайной бесповторной выборки, получено следующее распределение предприятий по росту производительности труда (в процентах по отношению к предыдущему году):

Рост производительности труда, %	13–17	17–21	21–25	25–29	29–33	33–37	Итого:
Число предприятий

Используя -критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X – рост производительности труда – распределена равномерно.

Вариант №10

1. В группе 14 человек, 4 из которых неуспевающих. По списку вызывают сразу пять человек. Найти вероятность того, что два из них будут неуспевающими.

2. Вероятности выполнить норму для каждого из трех спортсменов соответственно равны 0,7; 0,8 и 0,9. Найти вероятность того, что ее выполнят хотя бы один из них.

3. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна 0,4, для второго и третьего стрелков эти вероятности равны по 0,6. Найти вероятность того, что все 3 стрелка поразят цель.

4. В телевизионном ателье имеется 4 кинескопа. Вероятность того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0,9, 0,85, 0,6, 0,8. Наудачу взятый кинескоп не выдержал гарантийный срок. Найти вероятность того, что этот кинескоп второго типа.

5. В цехе 10 моторов. Для каждого мотора вероятность того, что он в данный момент отключен равна 0,1. Найти вероятность того, что в данный момент включены 4 мотора.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,5, математическое ожидание М(Х) = 3,5 и дисперсия D(X) = 0,25. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), D(X), если задан ряд распределения случайной величины Х:

Х
Р(Х)	0,105	0,49	0,005	??

8. Студент купил 4 лотерейных билета. Вероятность выигрыша по одному билету равна 0,3. Найти закон распределения числа выигрышей.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	1	2	4	6
Y	2	2,5	2,3	2,1

Предполагая, что между X и Y имеется зависимость вида 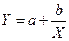найти неизвестные коэффициенты a и b по методу наименьших квадратов. Вычислить Y при .

10. Распределение 80 предприятий, выпускающих однотипную продукцию, по количеству реализованных товаров X (тыс. ед.) и цене на производимые товары Y (тыс. руб. за ед. продукции) представлено в таблице:

y x	10–20	20–30	30–40	40–50	50–60	Итого:
60–70
70–80
80–90
90–00
100–110
110–120
Итого:

Необходимо вычислить коэффициент корреляции и сделать вывод о тесноте и направлении связи между переменными X и Y.

Вариант №11

1. В ящике 11 деталей, 6 из которых стандартных. Из ящика вынимают сразу пять деталей. Найти вероятность того, что три из них будут стандартными.

2. Вероятности попадания в цель для каждого из трех орудий соответственно равны 0,9; 0,8 и 0,6. Найти вероятность того, что попадет в цель только два орудия.

3. Чему равна вероятность того, что при бросании трех игральных костей хотя бы на одной из них появится 6 очков?

4. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы 4, из второй 6, из третьей – 5 студентов. Вероятность того, что студент первой, второй и третьей группы попадают в сборную института, соответственно равны 0,9, 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. Найти вероятность того, что студент из третьей группы.

5. Вероятность того, что расход электроэнергии за одни сутки не превысит нормы равна 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,7, математическое ожидание М(Х) = 3,3 и дисперсия D(X) = 0,21. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), s(Х), если задан ряд распределения случайной величины Х:

Х
Р(Х)		??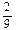

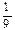
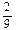
8. В конверте 14 карточек, среди которых 5 разыскиваемых. Наудачу отбирают 3 карточки. Найти закон распределения числа разыскиваемых карточек среди отобранных.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	-1	0	1	4
Y	0	1	2	5

Предполагая, что между X и Y имеется зависимость вида 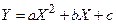найти неизвестные коэффициенты a, b и c по методу наименьших квадратов. Вычислить Y при .

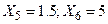10. Для нахождения средней цены продовольственной корзины из 1000 городов России по схеме собственно-случайной бесповторной выборки отобрали 100 городов. Полученные данные представлены в таблице:

Стоимость продовольственной корзины, тыс. руб.	Менее 1,0	1,0–1,2	1,2–1,4	1,4–1,6	Более 1,6	Итого
Число городов

Используя -критерий Пирсона, на уровне значимости α = 0,05 проверить гипотезу о том, что случайная величина Х – стоимость продовольственной корзины – распределена равномерно.

Вариант №12

1. Студент знает 10 вопросов из 25 вопросов программы. Найти вероятность того, что студент ответит на два из трех заданных вопросов.

2. Батарея из трех орудий производит залп по цели. Вероятности попадания в цель для каждого из них соответственно равны 0,7; 0,8 и 0,6. Найти вероятность того, что попадет в цель только одно орудие.

3. Три электрические лампочки последовательно включены в цепь. Вероятность того, что одна любая лампочка перегорит, если напряжение в сети превысит номинальное, равна 0,6. Найти вероятность того, что при повышенном напряжении тока в цепи не будет.

4. В мастерскую поступают телевизоры –75% от общего количества, стиральные машины - 15% и микроволновые печи – 10%. Вероятности того, что отремонтированный бытовой прибор прослужит в течение гарантийного срока, соответственно равны 0,9, 0,7 и 0,85. Найти вероятность того, что наудачу выбранный прибор сломался в гарантийное время.

5. Монету подбрасывают 6 раз. Найти вероятность того, что герб выпадет не менее двух раз.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,8, математическое ожидание М(Х) = 3,2 и дисперсия D(X) = 0,16. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), D(X), если задан ряд распределения случайной величины Х:

Х
Р(Х)	0,05	0,35	0,3	??

8. В группе 20 студентов, 8 из которых – отличники. На математическую олимпиаду наудачу отобраны 3 студента. Найти закон распределения числа отличников среди отобранных.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	0	1	5	6
Y	5	3	4	7

Предполагая, что между X и Y имеется зависимость вида 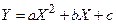найти неизвестные коэффициенты a, b и c по методу наименьших квадратов. Вычислить Y при .

10. Распределение 100 средних фермерских хозяйств по числу наемных рабочих X (чел.) и их средней месячной заработной плате на 1 человека Y (тыс. руб.) представлено в таблице:

y x	2 – 4	4 – 6	6 – 8	8 – 10	10 – 12	Итого
1–3
3–5
5–7
7–9
9–11
Итого

Необходимо вычислить коэффициент корреляции, на уровне значимости α = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y.

Вариант №13

1. В урне 3 белых и 8 черных шаров. Из урны вынимают сразу шесть шаров. Найти вероятность того, что три из них будут белыми.

2. Вероятности землетрясения в каждом из трех городов соответственно равны 0,2; 0,8 и 0,6. Найти вероятность того, что землетрясение произойдет только в двух городах.

3. Один стрелок делает 5 из 10 попаданий в цель, а другой – 9 из 10. Оба стрелка выстрелили одновременно. Найти вероятность попадания хотя бы одного попадания.

4. В библиотеке 10 учебников по математике разных лет издания: 2 - 1972г., 5 – 1983г и 3 – 1995г. Вероятности того, что учебники удовлетворяют программе, соответственно равны 0,6, 0,9, 0,95. Наудачу взятый учебник не соответствует программе. Найти вероятность того, что это учебник 1972 года.

5. Среднее число вызовов, поступающих на АТС за 1 мин., равно двум. Найти вероят-ность того, что за 4 мин. поступит не менее 5 вызовов.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,7, математическое ожидание М(Х) = 3,3 и дисперсия D(X) = 0,21. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), s(Х), если задан ряд распределения случайной величины Х:

Х
Р(Х)				??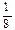

8. В конверте 18 карточек, среди которых 7 разыскиваемых. Наудачу отбирают 3 карточки. Найти закон распределения числа разыскиваемых карточек среди отобранных.

Дата добавления: 2014-12-24