В партии из 7 деталей имеется пять деталей первого сорта. Наудачу отобраны 4 детали для проверки. Найти закон распределения числа деталей первого сорта среди отобранных. 2 страница

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	0	1	5	6
Y	5	3	4	7

Предполагая, что между X и Y имеется зависимость вида 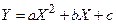найти неизвестные коэффициенты a, b и c по методу наименьших квадратов. Вычислить Y при .

10. Данные о продолжительности телефонных разговоров, отобранные по схеме собственно-случайной бесповторной выборки, приведены в таблице:

Время, мин	1,5––2,5	2,5––3,5	3,5––4,5	4,5––5,5	5,5––6,5	6,5––7,5	7,5––8,5	8,5––9,5	9,5– –10,5	Итого
Число разговоров

Используя -критерий Пирсона, уровне значимости α = 0,05 проверить гипотезу о том, что случайная величина Х – продолжительность телефонных разговоров – распределена равномерно.

Вариант №14

1. В группе 14 человек, 5 из которых неуспевающих. По списку вызывают сразу шесть человек. Найти вероятность того, что два из них будут неуспевающими.

2. Вероятности выполнить норму для каждого из трех спортсменов соответственно равны 0,7; 0,85 и 0,9. Найти вероятность того, что ее выполнят только один из них.

3. Вероятность того, при одном выстреле стрелок попадет в десятку, равна 0,6. Сколько выстрелов должен стрелок, чтобы с вероятностью не менее 0,8 он попал в десятку хотя бы один раз?

4. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятности того, что деталь попадет к одному из них, соответственно равны 0,6 и 0,4.Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,96, а вторым 0,78. Годная деталь при проверке была признана не стандартной. Найти вероятность того, что эту деталь проверил первый контролер.

5. В новом микрорайоне построен новый дом, в котором 500. Вероятность продажи квартиры в доме равна 0,9. Найти вероятность того, что продано 490.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,4, математическое ожидание М(Х) = 3,6 и дисперсия D(X) = 0,24. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), D(X), если задан ряд распределения случайной величины Х:

Х
Р(Х)	0,18	0,22	??	0,2

8. Три друга пришли сдавать экзамен. Вероятности успешной сдачи для каждого соответственно равны 0,7; 0,8; 0,5. Найти закон распределения числа успешно сдавших экзамен среди них.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	1	2	-1	3
Y	2	3	1	4

Предполагая, что между X и Y имеется зависимость вида 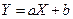найти неизвестные коэффициенты a и b по методу наименьших квадратов. Вычислить Y при .

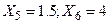10. Распределение 100 новых видов тарифов на сотовую связь всех известных мобильных систем X (ден. ед.) и выручка от них Y (ден. ед.) приводится в таблице:

y x							Итого
Итого

Необходимо вычислить коэффициент корреляции и сделать вывод о тесноте и направлении связи между переменными X и Y.

Вариант №15

1. В ящике 15 деталей, 9 из которых стандартных. Из ящика вынимают сразу шесть деталей. Найти вероятность того, что три из них будут стандартными.

2. Вероятности попадания в цель для каждого из трех орудий соответственно равны 0,9; 0,8 и 0,55. Найти вероятность того, что попадет в цель хотя бы одно орудие.

3. В типографии имеется 4 плоско-печатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,7. Найти вероятность того, что в данный момент работает хотя бы одна машина.

4. В группе спортсменов 15 лыжников, 7 велосипедистов и 3 бегуна. Вероятности выполнить квалификационную норму, соответственно равны 0,65, 0,8, 0,9. Найти вероятность того, что выбранный наудачу спортсмен выполнит норму.

5. Вероятность поражения мишени стрелком при одном выстреле 0,75. Найти вероятность того, что при 5 выстрелах стрелок поразит мишень не менее 2 раз.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,6, математическое ожидание М(Х) = 3,4 и дисперсия D(X) = 0,24. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), s(Х), если задан ряд распределения случайной величины Х:

Х
Р(Х)				??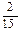

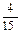
8. Производится ряд выстрелов по мишени с вероятностью попадания 0,7 при каждом выстреле. Стрельба ведется до первого попадания, но не свыше 4 выстрелов. Найти закон распределения числа произведенных выстрелов.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	1	2	4	6
Y	2	2,5	2,3	2,1

Предполагая, что между X и Y имеется зависимость вида 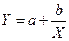найти неизвестные коэффициенты a и b по методу наименьших квадратов. Вычислить Y при .

10. Для нахождения среднего времени прорастания семян из большой партии по схеме собственно-случайной бесповторной выборки было отобрано 200 семян. Распределение семян по времени их прорастания представлено в таблице:

Время прорастания, дни	Менее	4–6	6–8	8–10	10–12	12–14	Более 14	Итого
Число семян

Используя -критерий Пирсона, уровне значимости α = 0,05 проверить гипотезу о том, что случайная величина Х – время прорастания семян – распределена равномерно.

Вариант №16

1. Студент знает 15 вопросов из 25 вопросов программы. Найти вероятность того, что студент ответит на два из четырех заданных вопросов.

2. Батарея из трех орудий производит залп по цели. Вероятности попадания в цель для каждого из них соответственно равны 0,7; 0,8 и 0,45. Найти вероятность того, что попадет в цель только два орудия.

3. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна 0,8, для второго и третьего стрелков эти вероятности соответственно равны 0,8 и 0,6. Найти вероятность того, что только два стрелка поразят цель.

4. В телевизионном ателье имеется 4 кинескопа. Вероятность того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0,8, 0,85, 0,9, 0,95. Найти вероятность того, что наудачу взятый кинескоп выдержит гарантийный срок службы.

5. В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен равна 0,8. Найти вероятность того, что в данный момент включены 4 мотора.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,9, математическое ожидание М(Х) = 2,2 и дисперсия D(X) = 0,36. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), D(X), если задан ряд распределения случайной величины Х:

Х	-2	-1
Р(Х)				??

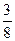
8. Вероятность попадания в цель из орудия при первом выстреле равна 0,1, при втором – 0,4, при третьем – 0,7. Найти закон распределения числа попаданий в цель, если произведено три выстрела.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	-1	0	1	4
Y	0	1	2	5

Предполагая, что между X и Y имеется зависимость вида 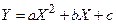найти неизвестные коэффициенты a, b и c по методу наименьших квадратов. Вычислить Y при .

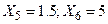10. Распределение 50 курящих мужчин по количеству выкуриваемых в день сигарет X (штук) и продолжительности жизни Y (лет) представлено в таблице:

y x	Менее 60	60–65	65–70	70 –75	Более 75	Итого
Менее 10
10–20
20–30
30–40
Более 40
Итого

Необходимо: вычислить коэффициент корреляции и сделать вывод о тесноте и направлении связи между переменными X и Y.

Вариант №17

1. В урне 5 белых и 9 черных шаров. Из урны вынимают сразу шесть шаров. Найти вероятность того, что два из них будут белыми.

2. Вероятности землетрясения в каждом из трех городов соответственно равны 0,1; 0,8 и 0,6. Найти вероятность того, что землетрясение произойдет хотя бы в одном городе.

3. В студии телевидении 3 телевизионных камеры. Для каждой камеры вероятность, что она включена в данный момент равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера.

4. Две перфораторщицы набили по одинаковому комплекту перфокарт. Вероятности того, что каждая из них допустит ошибку соответственно равны 0,05, 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица.

5. Всхожесть семян огурцов равна 0,8. Найти вероятность того, что среди пяти посеянных семян взойдут не менее 4.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,9, математическое ожидание М(Х) = 3,1 и дисперсия D(X) = 0,09. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), D(X), если задан ряд распределения случайной величины Х:

Х
Р(Х)	0,27	0,03	??	0,2

8. В партии из 7 деталей имеется пять деталей первого сорта. Наудачу отобраны 4 детали для проверки. Найти закон распределения числа деталей первого сорта среди отобранных.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	0	1	5	6
Y	5	3	4	7

Предполагая, что между X и Y имеется зависимость вида 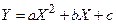найти неизвестные коэффициенты a, b и c по методу наименьших квадратов. Вычислить Y при .

10. По схеме собственно-случайной бесповторной выборки из 1500 участников соревнования было отобрано 100 человек. Их распределение по числу набранных баллов дано в таблице:

Число набранных баллов	52– –56	56– –60	60– –64	64– –68	68–72	72–76	Итого
Число участников

Используя -критерий Пирсона, на уровне значимости α = 0,05 проверить гипотезу о том, что случайная величина Х – число набранных баллов – распределена равномерно.

Вариант №18

1. В группе 20 человек, 4 из которых неуспевающих. По списку вызывают сразу шесть человек. Найти вероятность того, что три из них будут неуспевающими.

2. Вероятности выполнить норму для каждого из трех спортсменов соответственно равны 0,85; 0,8 и 0,9. Найти вероятность того, что ее выполнят только два из них.

3. Три стрелка произвели залп по цели. Вероятности поражения цели каждым стрелком соответственно равны 0,8, 0,9, 0,6. Найти вероятность того, что только один стрелок поразит цель.

4. На предприятии работают две бригады рабочих: первая производит ¾ продукции с процентом брака 4%, вторая - ¼ продукции с процентом брака 6%. Найти вероятность того, что наугад взятое бракованное изделие изготовлено второй бригадой.

5. Институт выпускает 70% специалистов высокого класса. Найти вероятность того, что среди 1000 выпущенных специалистов окажется 652 высокого класса.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,5, математическое ожидание М(Х) = 3,5 и дисперсия D(X) = 0,25. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), D(X), если задан ряд распределения случайной величины Х:

Х
Р(Х)	0,15	0,25	0,5	??

8. Студент купил 3 лотерейных билета. Вероятность выигрыша по одному билету равна 0,6. Найти закон распределения числа выигрышей.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	1	2	-1	3
Y	2	3	1	4

Предполагая, что между X и Y имеется зависимость вида 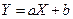найти неизвестные коэффициенты a и b по методу наименьших квадратов. Вычислить Y при .

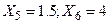10. В таблице приведено распределение 120 коров по дневному надою Y (в кг) и по жирности X (в %):

y x						Итого
3,3
3,5
3,7
3,9
4,1
Итого

Необходимо вычислить коэффициент корреляции и сделать вывод о тесноте и направлении связи между переменными X и Y.

Вариант №19

1. В ящике 18 деталей, 12 из которых стандартных. Из ящика вынимают сразу семь деталей. Найти вероятность того, что три из них будут стандартными.

2. Вероятности попадания в цель для каждого из трех орудий соответственно равны 0,9; 0,9 и 0,6. Найти вероятность того, что попадет в цель только одно орудие.

3. Один стрелок делает 80% попаданий в цель, а другой – 90%. Оба стрелка выстрелили одновременно. Найти вероятность попадания хотя бы одного попадания.

4. В библиотеке 90 учебников по математике разных лет издания: 25 - 1972г., 35 – 1983г и 30 – 1995г. Вероятности того, что учебники удовлетворяют программе соответственно равны 0,6, 0,7, 0,8. Наудачу взятый учебник соответствует программе. Найти вероятность того, что это учебник 1983 года.

5. Среднее число вызовов, поступающих на АТС за 1 мин., равно двум. Найти вероятность того, что за 3 мин. Поступит менее 4 вызовов.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,3, математическое ожидание М(Х) = 3,7 и дисперсия D(X) = 0,21. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), D(X), если задан ряд распределения случайной величины Х:

Х
Р(Х)	??	0,15	0,45	0,2

8. Производится ряд выстрелов по мишени с вероятностью попадания 0,8 при каждом. Стрельба ведётся до первого попадания в мишень, но не более четырёх выстрелов. Найти закон распределения числа произведённых выстрелов.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	-1	0	1	4
Y	0	1	2	5

Предполагая, что между X и Y имеется зависимость вида 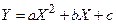найти неизвестные коэффициенты a, b и c по методу наименьших квадратов. Вычислить Y при .

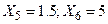10. Для нахождения средней стоимости компьютера определенной комплектации из 500 компьютерных магазинов региона по схеме собственно-случайной бесповторной выборки было отобрано 100 магазинов. Распределение компьютеров по их стоимости представлено в таблице:

Стоимость компьютера, тыс. руб.	10– –12	12– –14	14–16	16– –18	18– –20	20–22	Итого
Число магазинов

Используя -критерий Пирсона, на уровне значимости α = 0,05 проверить гипотезу о том, что случайная величина Х – стоимость компьютера – распределена равномерно.

Вариант №20

1. Студент знает 20 вопросов из 30 вопросов программы. Найти вероятность того, что студент ответит на два из четырех заданных вопросов.

2. Батарея из трех орудий производит залп по цели. Вероятности попадания в цель для каждого из них соответственно равны 0,4; 0,8 и 0,6. Найти вероятность того, что попадет в цель хотя бы одно орудие.

3. Предприятие обеспечивает регулярный выпуск комплектующих от двух смежников. Вероятность отказа в поставке продукции от первых смежников равна 0,05, от второго – 0,08. Найти вероятность отказа хотя бы одного.

4. В корзине 3 сорта яблок: 20 – первого, 15 – второго и 25 – третьего. Вероятность высокого содержания сахара в каждом из них соответственно равны 0,5, 0,6, 0,7. Наудачу взятое яблоко оказалось с высоким содержанием сахара. Найти, что это яблоко 1 сорта.

5. Станок – автомат штампует детали. Вероятность, что изготовленная деталь бракованная равна 0,01. Найти вероятность того, что среди 200 деталей окажется 4 бракованных.

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,1, математическое ожидание М(Х) = 3,9 и дисперсия D(X) = 0,09. Составить закон распределения этой случайной величины.

7. Вычислить М(Х), s(Х), если задан ряд распределения случайной величины Х:

Х
Р(Х)	??	0,15	0,35	0,4

8. Испытуемый прибор состоит из трёх малонадёжных элементов. Отказы элементов независимы, а их вероятности равны соответственно 0,1; 0,2; 0,25. Найти закон распределения числа отказавших за время Т элементов.

9. Результаты наблюдений над величинами X и Y приведены в следующей таблице:

X	-1	0	1	4
Y	0	1	2	5

Предполагая, что между X и Y имеется зависимость вида 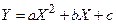найти неизвестные коэффициенты a, b и c по методу наименьших квадратов. Вычислить Y при .

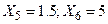10. Распределение 50 городов по численности населения X (тыс. чел.) и среднемесячному доходу на одного человека Y (тыс. руб.) представлено в таблице:

y x	2–3	3 – 4	4 – 5	5 – 6	6 – 7	7–8	Итого
0–50
50–100
100–150
150–200
200–250 Более 250
Итого

Необходимо вычислить коэффициент корреляции и сделать вывод о тесноте и направлении связи между переменными X и Y.

Дата добавления: 2014-12-24