Абсолютные показатели вариации

К примерам вариаций относятся следующие показатели: 1. размах вариаций 2. среднее линейное отклонение 3. среднее квадратическое отклонение 4. дисперсия5. Коэффициент. К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение (стандартное отклонение). Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака. Среднее линейное отклонение (d)представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от средней величины. Если ряд не сгруппирован, то рассчитывается простое среднее линейное отклонение:

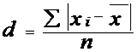.Для вариационного ряда с неравными частотами следует использовать взвешенное среднее линейное отклонение, где весами выступают частоты соответствующих вариант
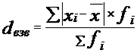. Дисперсией (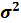) называется средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней величины. По несгруппированным данным она рассчитывается по формуле: 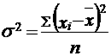, (7.3) для сгруппированных данных с неравными частотами: 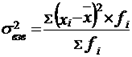(7.4) Квадратный корень из дисперсии называется средним квадратическим отклонением (стандартныым отклонением). Среднее квадратическое отклонение для несгруппированных данных рассчитывается по формуле: 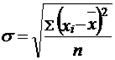(7.5) для сгруппированных данных с неравными частотами: 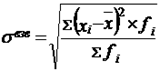(7.6) Абсолютные показатели вариации за исключением дисперсии имеют те же единицы измерения, что и исследуемый показатель вариационного ряда. Это затрудняет сравнение вариации в статистических совокупностях, где признаки выражены в разных единицах измерения (например, дифференциация доходов населения разных стран в национальной валюте). Поэтому, если экономическая интерпретация, например, среднего линейного отклонения проста и понятна, то в случае с дисперсией - затруднена. Если признак характеризует численность работников и единицей измерения является количество человек, то дисперсия будет измеряться количеством человек в квадрате. Однако дисперсия применяется в статистическом анализе гораздо чаще, чем другие показатели вариации. Она используется в методе наименьших квадратов, в корреляционном, регрессионном, дисперсионном анализе и выборочном наблюдении. Дисперсия может быть рассчитана упрощенным способом как разность между средним значением квадратов индивидуальных значений признака и квадрата среднего значения этого же признака: 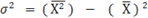(7.7) Если совокупность единиц наблюдения разделена по какому-либо признаку на некоторое количество групп, то можно оценить зависимость вариации значений какого-либо показателя, характеризующую единицы наблюдения, от признака, положенного в основу группировки. Общая дисперсия характеризует вариацию значений признака за счет всех факторов,как положенного в основу группировки, так и остальных не учтенных в группировке, но действующих на исследуемый признак. Внутригрупповые дисперсии характеризуют вариацию значений исследуемого признака внутри групп независимо от того, какое значение принимает группировочный признак(оценивается влияние на показатель факторов, отличных от группировочного). Мсжгрупповая дисперсия характеризует вариацию значений показателя за счет действия на него только группировочного признака. Между средней из внутригрупповых дисперсий, межгрупповой и общей дисперсиями существует зависимость, известная как «правило сложения дисперсий»: общая дисперсия равна сумме межгрупповой и средней внутригрупповой.

Дата добавления: 2014-12-24