Проверка гипотезы о равенстве средних двух выборок при помощи критерия Стьюдента

Проверка гипотеза о равенстве средних двух выборок проводится использованием режима работы «Парный двухвыборочный t-тест для средних», который запускается через действие меню «Сервис/Анализ данных…».

Суть проверки в примере заключается в проверке влияния группопорождающего признака (гум. и техн.) на величину оценки шкалы 2. Если будет доказано, что средние двух выборок a_гум и a_техн по критерию Стьюдента равны, то это означает, что показатели шкалы 2 не зависят от группопорождающего признака, т.е. все равно с кого снимать оказания по шкале 2 с респондента «гум» или с респондента «техн» (результат или вывод будет одинаков).

Диалоговое окно режима с заданными параметрами приведено на рис.10. При использовании этого режима необходимо помнить, что выборочные данные должны быть парными.

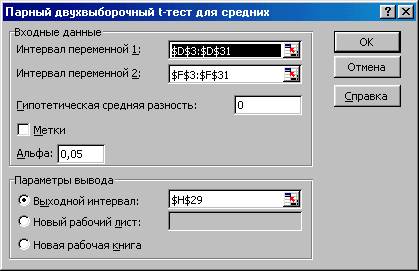
Рис.10. Вид заполненного окна режима оценки гипотезы оценки равенства средних двух выборок.

Рассчитанные в данном режиме показатели приведены в следующей таблице:

Парный двухвыборочный t-тест для средних
	Переменная 1	Переменная 2
Среднее	11,69	11,14
Дисперсия	3,44	3,98
Наблюдения
Корреляция Пирсона	0,958
Гипотетическая разность средних
df
t-статистика	5,19
P(T<=t) одностороннее	0,0000082
t критическое одностороннее	1,70
P(T<=t) двухстороннее	0,0000165
t критическое двухстороннее	2,05

Из полученной таблицы видно, что расчетное значение t-критерия t_р=5,19, а критическая область образуется двумя интервалами (-∞; -2,05) и (+2,05; +∞). Так как t_р попадает в критический интервал (+2,05; +∞), то гипотезу о равенстве средних a_гум и a_техн отвергаем, т.е. отнесение респондентов к группе гум. или техн. влияет на величину показателя шкалы 2.

Результаты и выводы по заданию 2 включить в итоговый документWord.

Решение задания 3

Дата добавления: 2014-12-24