АВС – трійки

Радикал числа

Гіпотеза АВС була сформульована в 1986 році, Массером и Остерле. На думку Сержа Ленга вона представляє собою одну з найкращих математичних гіпотез ХХ століття. Для її формулювання нам знадобляться визначення радикала натурального числа.

Визначення. Радикалом натурального числа (в анголомовному варіанті Radical of an integer) називають добуток усіх простих дільників данного числа

.

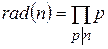За означенням .

Якщо відомо канонічне розкладання числа 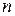на прості множники, то

.

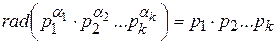Рівність має місце тоді і тільки тоді, коли 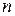вільне від квадратів, тобто коли

Приклад: , .

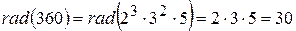Очевидні наступні властивості:

Якщо числа 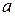і взаємно прості, то .

1. .

2. якщо , то .

Нехай - взаємно прості натуральні числа, такі що 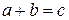. Такі тройки будемо називати допустимими.

Задамося питанням: що більше, найбільше з чисел допустимої тройки (число ) або радикал добутку елементів цієї тройки (в силу взаємної простоти її елементів )?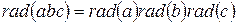

Наприклад, якщо взяти тройку , то 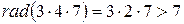. Анализ цього приклада дозволяє прийти до висновку, що якщо число вільне від квадратів, то радикал добутку завідома більше. Виявляється, що такі тройки, в яких радикал добутку більше, ніж , зустрічаються набагато частіше, ніж ті, в яких має місце зворотна нерівність.

Визначення. Тройка взаємно простих натуральних чисел , таких що 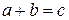називається 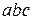-тройкою, якщо

.

Приклад: 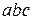-тройками являются тройки 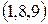, та інші.

Покажем це:

,

.

Може скластися уявлення, що всі 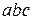-тройки починаються з одиниці, але це не так. 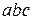-тройкою є тройка (4,121,125,).

Прямі обчислення показують, що серед допустимих троек, у яких , кількість 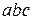-троек дорівнює 276. Оскільки їх не так багато, то природно виникає питання о їх конечності або нескінченності.

Виявляється, на це питання достатньо легко можна дати відповідь, виділив нескінчену серію 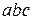-троек.

Дата добавления: 2014-12-24