
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Москва – 2013 2 страница
|
|
|
|
Задача 3.
Постройте аналитическую группировку предприятий табачной промышленности, характеризующую зависимость объема производства табачных изделий от влияния стоимости основных производственных фондов. Результаты изложите в табличной форме и проанализируйте их.
Решение: Используя результаты, полученные при решении 2-й задачи, построим аналитическую группировку предприятий, характеризующую зависимость объема производства табачных изделий от влияния стоимости основных производственных фондов.
Рассчитаем число предприятий в % к итогу и полученные результаты поместим в итоговую группировочную таблицу.
| Группы по стоимости основных фондов, млн. р. | Число предприятий | Число предприятий в % к итогу | Объем производства изделий, тыс. шт. | |
| всего | в среднем | |||
| 1,1 – 8,375 | 53,3 | 6810,94 | ||
| 8,375 – 15,65 | 30,0 | 8962,22 | ||
| 15,65 – 22,925 | 6,7 | |||
| 22,925 – 30,2 | 10,0 | 11666,67 | ||
| Итого | 100,0 | 8397,5 |
Анализ полученной таблицы позволяет сделать следующие выводы: числа в последнем столбце таблицы, показывающий средний объем производства в каждой из групп, увеличиваются, следовательно, с увеличением стоимости основных средств объем производства изделий возрастает, что позволяет предположить, что между указанными показателями существует прямая корреляционная связь.
Задача 4.
На основании группировки, построенной в пункте 2 задачи 2 рассчитайте:
а) относительные величины структуры (по двум любым показателям);
б) средний размер товарной продукции на одного работающего по каждой выделенной группе;
б) средний размер основных производственных фондов на одно предприятие по каждой выделенной группе;
2. Результаты расчетов изложите в той же сводной групповой таблице, где и результаты группировки, дополнив ее соответствующими графами.
Решение: Используя результаты, полученные в п. 2 задачи 2, рассчитаем по объему производства и товарной продукции относительные величины структуры.
Для этого значения по каждой группе разделим на итоговые значения, выразив результат в процентах.
Средний размер товарной продукции на одного работающего по каждой выделенной группе найдем, разделив стоимость товарной продукции на численность персонала.
Средний размер основных производственных фондов на одно предприятие по каждой выделенной группе найдем, разделив размер основных фондов на число предприятий.
Результаты расчетов представим в сводной групповой таблице
| Группы по стоимости основных фондов, млн. р. | Число предприятий | Объем производства изделий, тыс. шт. | Товарная продукция в оптовых ценах предприятий, млн. р. | Численность персонала, чел. | Товарная продукция на одного работающего, тыс. р. | Стоимость ОПФ на одно предприятие | ||
| всего | в % к итогу | всего | в % к итогу | |||||
| 1,1 – 8,375 | 43,26 | 697,8 | 36,51 | 69,8 | 6810,94 | |||
| 8,375 – 15,65 | 32,0 | 609,9 | 31,91 | 99,527 | 8962,22 | |||
| 15,65 – 22,925 | 10,8 | 224,6 | 11,75 | 183,5 | ||||
| 22,925 - 30,2 | 13,94 | 19,83 | 130,017 | 11666,67 | ||||
| Итого | 100,0 | 1911,3 | 100,0 | 94,32 | 8397,5 |
По результатам расчетов можно сделать следующие выводы: доминирующее положение по объему производства занимают предприятия, имеющие основные фонды в размере от 1,1 до 8,375 млн. р. Наибольший удельный вес товарной продукции в ее общей стоимости занимают предприятия, имеющие основные фонды в размере от 8,375 до 15,65 млн. р. и 1,1 до 8,375 млн. р. – 31,91% и 36,51% всей товарной продукции.
Задача 5.
1. По исходным данным, представленным в таблице N1 (Вашего варианта) постройте ряд распределения по численности промышленно-производственного персонала, образовав не более шести групп предприятий с равными интервалами. Результаты представьте в табличной форме.
2. По данным ряда распределения (см. пункт 1) постройте гистограмму и полигон распределения и сформулируйте краткие выводы.
3. По полученному ряду распределения определите среднюю численность промышленно-производственного персонала, моду, медиану, квартили и коэффициент вариации.
Решение: Построим ряд распределения по численности промышленно-производственного персонала, образовав 5 групп предприятий с равными интервалами
Обозначим через х численность персонала. Определим размах варьирования признака х.
х min = 291; х max = 1535; R = х max - х min = 1535 – 291 = 1244.
Величина интервала равна h = R: m = 1244: 5 = 249.
Выделим 5 групп с равными интервалами и подсчитаем количество вариантов в каждой из них.
1-я группа: [291; 540]
2- я группа: [540; 789]
3-я группа: [789; 1038]
4-я группа: [1038; 1287]
5-я группа: [1287; 1536]
Составим расчетную группировочную таблицу.
| Группа | № предприятия | Среднесписочная численность промышленно-производственного персонала, чел. |
| 291 - 540 | ||
| Количество в группе | ||
| 540 - 789 | ||
| Количество в группе | ||
| 789 - 1038 | ||
| Количество в группе | ||
| 1038 - 1287 | ||
| Количество в группе | ||
| 1287 - 1536 | ||
| Количество в группе | ||
| Общее количество |
Вычислим середины интервалов, сложив начало и конец интервала и разделив результат на 2. Вычислим относительные частоты, разделив частоту в интервале на общую сумму частот. Получим следующий интервальный ряд распределения.
| Интервал | 291 - 540 | 540 - 789 | 789 - 1038 | 1038 - 1287 | 1287 - 1536 | Сумма |
Частота в интервале, 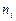
| ||||||
| Середина интервала | 415,5 | 664,5 | 913,5 | 1162,5 | 1411,5 | |
| Относительная частота | 0,46 | 0,3 | 0,07 | 0,07 | 0,10 |
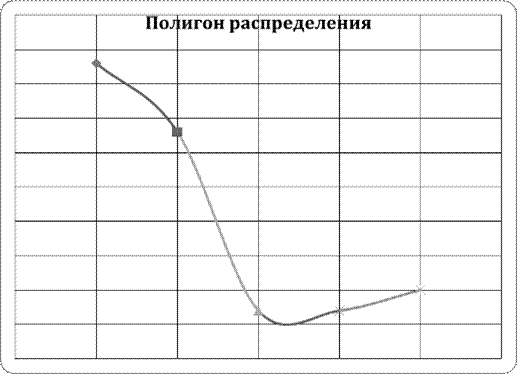
Построим полигон частот, отложив по горизонтальной оси значения 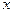 , а по вертикальной - соответствующие значения относительных частот.
, а по вертикальной - соответствующие значения относительных частот.
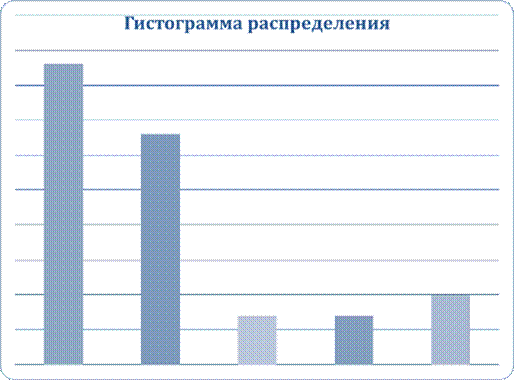
Построим гистограмму частот, отложив по горизонтальной оси интервалы изменения признака, а по вертикальной - соответствующие значения относительных частот.
Найдем по полученному ряду распределения среднюю численность промышленно-производственного персонала, моду, медиану, квартили и коэффициент вариации. Среднюю найдем по формуле:
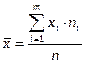 ,
,
где n - объем выборки, m - количество интервалов, yi - середина i-го интервала.
Найдем дисперсию по формуле:
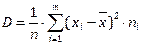
Составим вспомогательную таблицу
| Интервалы | Частоты, ni | Относительные частоты | Накопленные частоты | Середина интервала, xi | xi × ni | (x – 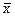 )2× ni )2× ni
|
| 291 – 540 | 0,46 | 415,5 | 926846,06 | |||
| 540 – 789 | 0,3 | 664,5 | 5980,5 | 620,01 | ||
| 789 – 1038 | 0,07 | 913,5 | 115872,98 | |||
| 1038 – 1287 | 0,07 | 1162,5 | 479612,18 | |||
| 1287 – 1536 | 0,10 | 1411,5 | 4234,5 | 1637033,07 | ||
| 3159984,3 |
Получим: 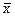 = 20184: 30 = 672,8 чел.
= 20184: 30 = 672,8 чел.
Dв =3159984,3: 30 = 105332,81.
Вычислим среднее квадратичное отклонение:
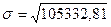 = 325 чел.
= 325 чел.
Вычислим коэффициент вариации.
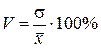 = 325: 672,8 × 100% = 48,3%.
= 325: 672,8 × 100% = 48,3%.
Определим моду. Модальный интервал - это интервал с наибольшей частотой. В нашем случае это интервал (291; 540). Значение моды определим по формуле:
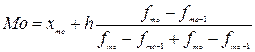
где 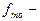 частота в модальном интервале,
частота в модальном интервале, 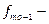 частота в интервале, предшествующем модальному,
частота в интервале, предшествующем модальному, 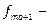 частота в интервале, следующим за модальным,
частота в интервале, следующим за модальным, 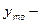 нижняя граница модального интервала, h - величина модального интервала. В нашем случае:
нижняя граница модального интервала, h - величина модального интервала. В нашем случае: 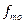 = 14,
= 14, 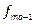 = 0,
= 0, 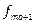 = 9, h = 249.
= 9, h = 249.
Получим: 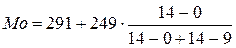 = 474,5 чел.
= 474,5 чел.
Определим медиану. Медианный интервал - это интервал, в котором значение накопленной частоты достигает значения, равного половине суммы частот, т.е.
30: 2 = 15. Вычислим накопленные частоты.
S 1 = 14; S 2 = 14 + 9 = 23.
Таким образом, медианный интервал: (540; 789). Значение медианы определим по формуле:
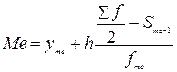
где 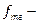 частота медианного интервала,
частота медианного интервала, 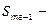 накопленная частота в интервале, предшествующем медианному,
накопленная частота в интервале, предшествующем медианному, 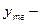 нижняя граница медианного интервала,
нижняя граница медианного интервала,
h - величина медианного интервала. В нашем случае: 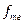 = 9,
= 9, 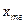 = 540,
= 540, 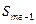 = 14.
= 14.
Получим: 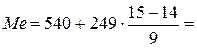 = 567,7 чел.
= 567,7 чел.
| Интервалы | Частоты, ni | Относительные частоты | Накопленные частоты | Середина интервала, xi | xi × ni | (x – 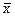 )2× ni )2× ni
|
| 291 - 540 | 0,46 | 415,5 | 926846,06 | |||
| 540 - 789 | 0,3 | 664,5 | 5980,5 | 620,01 | ||
| 789 - 1038 | 0,07 | 913,5 | 115872,98 | |||
| 1038 - 1287 | 0,07 | 1162,5 | 479612,18 | |||
| 1287 - 1536 | 0,10 | 1411,5 | 4234,5 | 1637033,07 | ||
| 3159984,3 |
Для расчета квартилей воспользуемся формулами:
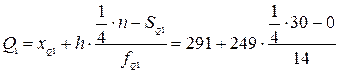 = 424,4 чел.
= 424,4 чел.
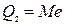 = 567,7 чел.
= 567,7 чел.
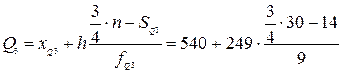 = 775,2 чел.
= 775,2 чел.
Задача 7.
По данным о среднегодовой стоимости промышленно-производственных основных фондов и товарной продукции (возьмите 15 предприятий Вашего варианта из таблицы 1) выполните следующее:
1) постройте по этим показателям ряд параллельных данных; определите наличие связи, изобразив графически парную связь между результативным и факторным признаками;
2) рассчитайте парный линейный коэффициенты корреляции связи между изучаемыми признаками, а также ранговый коэффициент корреляции;
3) выберите уравнение связи и вычислите параметры уравнения регрессии, рассчитайте на его основе теоретические значения товарной продукции и нанесите эти значения на построенный в пункте 1 график;
4) Дайте экономическую интерпретацию уравнения связи;
5) Все промежуточные расчеты изложите в табличной форме.
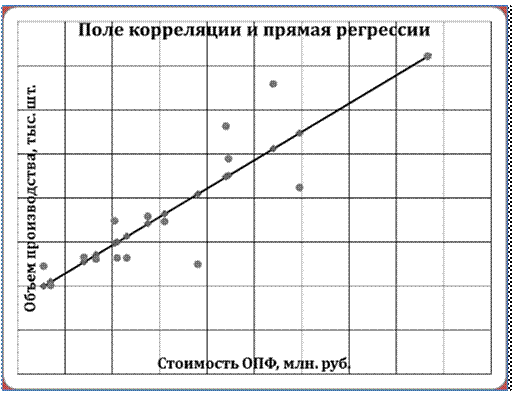
Решение: Для анализа выберем следующие показатели: x – стоимость основных производственных фондов – факторный признак и y – объем производства изделий – результативный признак.
Изобразим зависимость объема производства от среднегодовой стоимости ОПФ в виде точечной диаграммы.

Точки на приведенном графике располагаются вблизи некоторой прямой, что позволяет предположить, что между указанными показателями существует линейная зависимость.
Измерим степень тесноты связи между факторным и результативным признаками.
Определим линейный коэффициент парной корреляции по следующей формуле:
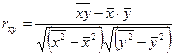
Составим вспомогательную таблицу.
| № предприятия | y | х | y2 | х2 | x·y |
| 4,1 | 16,81 | ||||
| 1,4 | 1,96 | ||||
| 17,3 | 299,29 | ||||
| 8,9 | 79,21 | ||||
| 4,2 | 17,64 | ||||
| 4,6 | 21,16 | ||||
| 1,1 | 1,21 | ||||
| 6,2 | 38,44 | ||||
| 2,8 | 7,84 | ||||
| 11,9 | 141,61 | ||||
| 5,5 | 30,25 | 39297,5 | |||
| 3,3 | 10,89 | 17209,5 | |||
| 10,8 | 116,64 | ||||
| 8,8 | 77,44 | ||||
| 1,6 | 2,56 | ||||
| Сумма | 92,5 | 862,95 | |||
| Среднее | 7997,7 | 6,2 | 74369651,67 | 57,53 | 59816,2 |
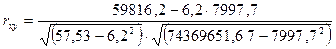 = 0.726
= 0.726
По значению линейного коэффициента парной корреляции можно заключить, что между рассматриваемыми признаками существует тесная прямая корреляционная связь.
Вычислим выборочный коэффициент ранговой корреляции Спирмена.
Расположим значения x в порядке возрастания. Пронумеруем значения строки значений x от 1 до 15. Пронумеруем также значения строки y от 1 до 15, учитывая порядок их расположения.
Получим следующую таблицу:
| Ранг | |||||||||||||||
| x | 1,1 | 1,4 | 1,6 | 2,8 | 3,3 | 4,1 | 4,2 | 4,6 | 5,5 | 6,2 | 8,8 | 8,9 | 10,8 | 11,9 | 17,3 |
| Ранг | |||||||||||||||
| y |
Вычислим значения d i.
d 1 = 1 – 7 = -6; d 2 = 2 – 2 = 0; d 3 = 3 – 15 = -12;
d 4 = 4 – 9 = -5; d 5 = 5 – 12 = -7; d 6 = 6 – 1 = 5;
d 7 = 7 – 5 = 2; d 8 = 8 – 6 = 2; d 9 = 9 – 11 = -2;
d 10 = 10 – 8 = 2; d 11 = 11 – 14 = -3; d 12 = 12 – 4 = 8;
d 13 = 13 – 13 =0; d 14 = 14 – 10 = 4; d 15 = 15 – 3 = 12.
Вычислим 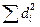
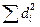 = (-6)2 + 02 + (-12)2 + (-5)2 + (-7)2 + 52 + 22 + 22 + (-2)2 + 22+ (-3)2 + 82 + 02 + 42 + 122 = 528.
= (-6)2 + 02 + (-12)2 + (-5)2 + (-7)2 + 52 + 22 + 22 + (-2)2 + 22+ (-3)2 + 82 + 02 + 42 + 122 = 528.
Выборочный коэффициент ранговой корреляции Спирмена найдем по формуле:
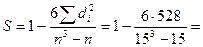 = 0,9
= 0,9
Связь сильная.
Составим уравнение линейной регрессии в виде: 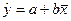 .
.
Значения параметров a и b линейной модели определим, используя данные расчетной таблицы.
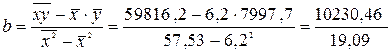 = 535,9.
= 535,9.
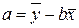 = 7997,7 – 535,9×6,2 = 4675,12.
= 7997,7 – 535,9×6,2 = 4675,12.
Уравнение регрессии имеет вид: 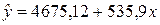 .
.
Таким образом, с увеличением стоимости ОПФ на 1 млн. р. выпуск продукции в целом возрастает на 535,9 шт.
Рассчитаем на основе полученного уравнения регрессии теоретические значения товарной продукции.
| Стоимость основных производственных фондов, млн. руб. | Объем производства изделий, тыс. шт. | Теоретические значения y |
| 4.1 | 6872,31 | |
| 1.4 | 5425,38 | |
| 17.3 | 13946,19 | |
| 8.9 | 9444,63 | |
| 4.2 | 6925,9 | |
| 4.6 | 7140,26 | |
| 1.1 | 5264,61 | |
| 6.2 | 7997,9 | |
| 2.8 | 6175,64 | |
| 11.9 | 11052,33 | |
| 5.5 | 7622,57 | |
| 3.3 | 6443,59 | |
| 10.8 | 10462,84 | |
| 8.8 | 9391,04 | |
| 1.6 | 5532,56 |
Нанесем эти значения на построенный в пункте 1 график.
Полученное уравнение регрессии 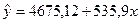 показывает, что с увеличением стоимости ОПФ на 1 млн. р. выпуск продукции в целом возрастает на 535,9 шт.
показывает, что с увеличением стоимости ОПФ на 1 млн. р. выпуск продукции в целом возрастает на 535,9 шт.
Задача 8.
По данным Вашего варианта выполните следующее:
1. Изобразите графически динамику ряда с помощью статистической кривой.
2. Вычислите по данным этого ряда аналитические показатели: абсолютные, относительные средние; результаты расчетов изложите в табличной форме.
3. Произведите сглаживание ряда динамики с помощью скользящей средней и аналитического выравнивания. Полученные данные нанесите на график (см. пункт 1).
4. Сформулируйте выводы относительно основной тенденции развития ряда динамики.
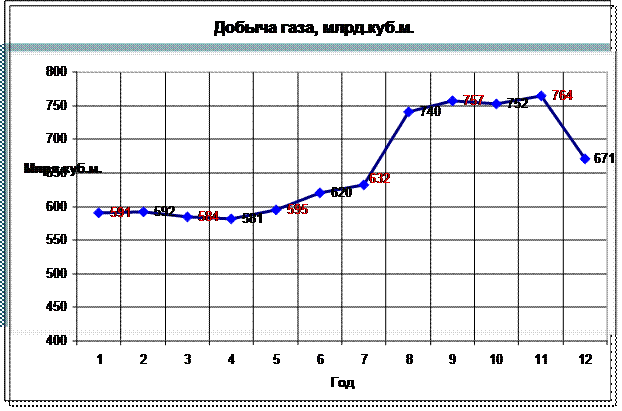
Решение: Изобразите графически динамику ряда с помощью статистической кривой.
Добыча газа (млрд.куб.м.) в Российской Федерации.
| Годы | Тыс. шт. |
Абсолютные приросты вычислим по формуле At = xt - x 0 (по базисной схеме) и at = xt – x t-1 (по цепной схеме). Темпы роста вычислим по формуле 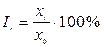 (по базисной схеме)
(по базисной схеме) 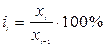 (по цепной схеме). Темпы прироста вычислим по формуле
(по цепной схеме). Темпы прироста вычислим по формуле 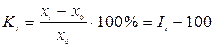 (по базисной схеме),
(по базисной схеме), 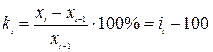 (по цепной схеме).
(по цепной схеме).
Полученные значения поместим в таблицу
| Годы | Добыча газа, млрд. куб. м | Абсолютные приросты, млрд. куб. м | Темпы роста, % | Темпы прироста, % | |||
| Базисн. | Цепные | Базисн. | Цепные | Базисн. | Цепные | ||
| - | - | - | - | - | - | ||
| 100,2 | 100,2 | 0,17 | 0,17 | ||||
| -7 | -8 | 99,8 | 98,6 | -1,2 | -1,4 | ||
| -10 | -3 | 98,3 | 99,5 | -1,7 | -0,5 | ||
| 100,7 | 102,4 | 0,7 | 2,4 | ||||
| 104,9 | 104,2 | 4,9 | 4,2 | ||||
| 106,9 | 101,9 | 6,9 | 1,9 | ||||
| 125,2 | 117,1 | 25,2 | 17,1 | ||||
| 128,1 | 102,3 | 28,1 | 2,3 | ||||
| -5 | 127,2 | 99,3 | 27,2 | -0,7 | |||
| 129,3 | 101,6 | 29,3 | 1,6 | ||||
| -93 | 113,5 | 87,8 | 13,5 | -12,2 | |||
| Сумма |
Вычислим среднегодовой уровень ряда динамики.
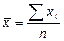 = 7879: 12 = 656,6 млрд. куб. м
= 7879: 12 = 656,6 млрд. куб. м
Определим среднегодовые абсолютный прирост, темпы роста и прироста добычи газа.
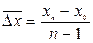 = (671 - 591): (12 - 1) = 7,3 млрд. куб. м.
= (671 - 591): (12 - 1) = 7,3 млрд. куб. м.
Вычислим средние темпы роста и прироста
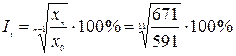 = 1,489·100 = 148,9%
= 1,489·100 = 148,9%
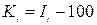 = 148,9 - 100 = 48,9%
= 148,9 - 100 = 48,9%
Произведем сглаживание ряда динамики трехзвенной скользящей средней.
Используем для этого формулы
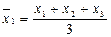 ,
, 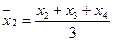 и т.д.
и т.д.
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 390; Нарушение авторских прав?; Мы поможем в написании вашей работы!