
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Москва – 2013 3 страница
|
|
|
|
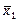 = (591 + 592 + 584): 3 = 589;
= (591 + 592 + 584): 3 = 589;
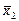 = (592 + 584 + 581): 3 = 585,7;
= (592 + 584 + 581): 3 = 585,7;
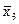 = (584 + 581 + 595): 3 = 413,0 и т.д.
= (584 + 581 + 595): 3 = 413,0 и т.д.
Полученные данные представим в виде таблицы:
| Годы | Добыча газа, млрд. куб. м | Выровненные уровни |
| - | ||
| 585,7 | ||
| 586,7 | ||
| 598,7 | ||
| 615,7 | ||
| 709,7 | ||
| 749,7 | ||
| 757,7 | ||
| - |
Построим графическое изображение полученных рядов.
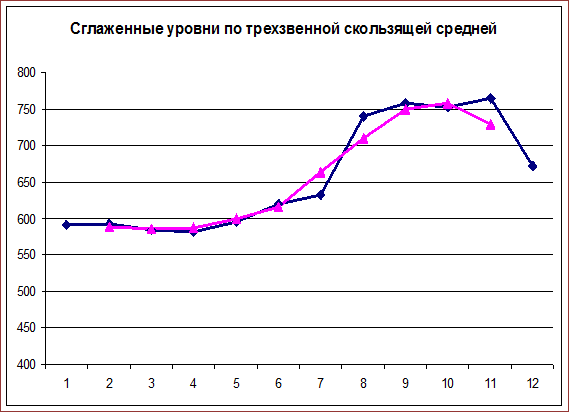
Произведем сглаживание ряда динамики с помощью аналитического выравнивания.
Составим вспомогательную таблицу.
| № п/п | Условный год t | Добыча газа, y | t2 | y2 | t×y |
| Сумма | - |
В качестве функции выравнивания выбрано уравнение прямой линии:
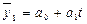
Параметры данного уравнения находим по упрощенным формулам:
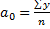
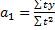
a0=7879÷12=656.58
a1=53679÷650=82.58
Уравнение регрессии имеет вид: 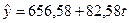 .
.
Рассчитаем на основе полученного уравнения регрессии теоретические значения товарной продукции.
| Условный год, t | Добыча газа, y | Теоретические значения y |
| 739.16 | ||
| 821.74 | ||
| 904.32 | ||
| 986.9 | ||
| 1069.48 | ||
| 1152.06 | ||
| 1234.64 | ||
| 1317.22 | ||
| 1399.8 | ||
| 1482.38 | ||
| 1564.96 | ||
| 1647.54 |
Нанесем эти значения на график.
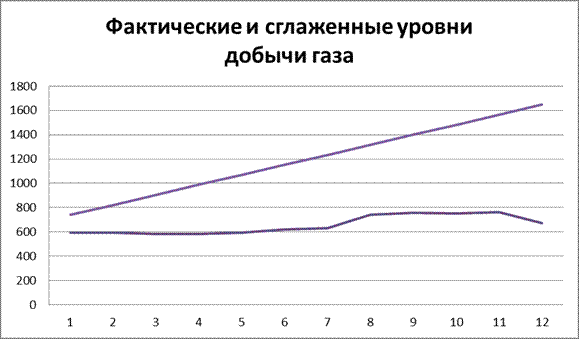
Анализ полученных результатов показывает, что в рассмотренный период наблюдалось увеличение добычи газа, хотя к концу рассматриваемого периода темп роста значительно снизился.
Задача 9.
По данным Вашего варианта выполните следующее:
а) исчислите индивидуальные цепные индексы цен;
б) исчислите сводные цепные индексы цен;
в) исчислите сводные цепные индексы товарооборота и физического объема проданных товаров;
г) исчислите сводный индекс цен в среднегармонической форме;
д) проверьте правильность расчетов, используя взаимосвязи индексов;
е) исчислите сводные базисные и цепные индексы цен с постоянными и переменными весами.
Решение: Рассчитаем цены за каждый период, разделив стоимость оборота на количество проданных товаров, выразив результат в рублях.
Например, найдем цену лука в январе:
302 × 1000: 754,6 = 400,2 руб.
Полученные значения поместим в таблицу.
| N п/п | Наимено-вание товара | Январь | Февраль | Март | Апрель | Май | ||||||
| кол-во продан-ных товаров, ц | обо-рот, тыс. руб. | кол-во про-дан-ных товаров, ц | обо-рот, тыс.руб. | кол-во про-данных товаров, ц | обо-рот, тыс. руб. | кол-во про-данных товаров, ц | Обо-рот, тыс. руб. | кол-во продан-ных товаров, ц | Обо-рот, тыс. руб. | |||
| Яблоки | 851.1 | 1007.4 | 373.9 | 295.8 | 302.2 | |||||||
| Говядина | 1068.8 | 911.6 | 1063.4 | 1205.9 | 981.8 | |||||||
| Баранина | 274.2 | 191.7 | 237.3 | 169.6 | 178.3 |
Вычислим индивидуальные индексы цен в феврале по сравнению с январем:
Яблоки: ip =(1813:1007,4):(1447:851,1)=1799,68:1700,15=1,059
Говядина: ip = (1823:911,6): (2031:1068,8) = 1999,78: 1900,26=1,052;
Баранина: ip = (479:191,7): (658:274,2) = 2498,69: 2399,71=1,041;
Определим сводный индекс цен.
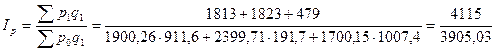 = 1,054 = 105,4%.
= 1,054 = 105,4%.
Определим сводный индекс товарооборота.
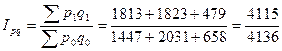 = 0,995 = 99,5%.
= 0,995 = 99,5%.
Определим сводный индекс физического объема проданных товаров.
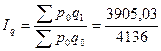 = 0,944 = 94,4%.
= 0,944 = 94,4%.
Вычислим сводный индекс цен в среднегармонической форме.
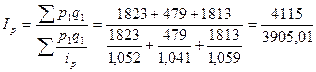 = 1,054 = 105,4%.
= 1,054 = 105,4%.
Проверим правильность расчетов, используя взаимосвязи индексов.
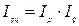 = 0,944 × 1,054 = 0,944 = 94,4%.
= 0,944 × 1,054 = 0,944 = 94,4%.
Вычислим индивидуальные индексы цен в марте по сравнению с февралем:
Яблоки: ip =2000,5:1799,68 =1,112
Говядина: ip = 2002,07: 1999,78 = 1,001;
Баранина: ip = 2498,95: 2498,69 = 1,00;
Определим сводный индекс цен.
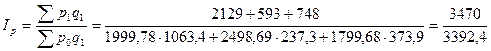 = 1,023 = 102,3%.
= 1,023 = 102,3%.
Определим сводный индекс товарооборота.
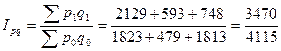 = 0,843 = 84,3%.
= 0,843 = 84,3%.
Определим сводный индекс физического объема проданных товаров.
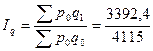 = 0,824 = 82,4%.
= 0,824 = 82,4%.
Вычислим сводный индекс цен в среднегармонической форме.
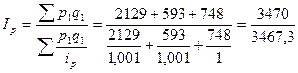 = 1,001 = 100,1%.
= 1,001 = 100,1%.
Проверим правильность расчетов, используя взаимосвязи индексов.
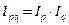 = 0,824 × 1,001 = 0,824.
= 0,824 × 1,001 = 0,824.
Вычислим индивидуальные индексы цен в апреле по сравнению с мартом:
Яблоки: ip =2349,56:2000,5=1,174
Говядина: ip = 2200,0: 2002,07 = 1,099;
Баранина: ip = 2742,64: 2502,11 = 1,096;
Определим сводный индекс цен.
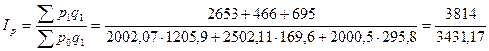 =
=
= 1,116= 111,6%.
Определим сводный индекс товарооборота.
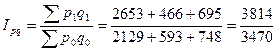 =1,099=109,9%.
=1,099=109,9%.
Определим сводный индекс физического объема проданных товаров.
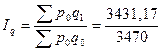 = 0,989 = 98,9%.
= 0,989 = 98,9%.
Вычислим сводный индекс цен в среднегармонической форме.
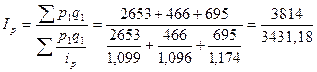 = 1,111 = 111,1%.
= 1,111 = 111,1%.
Проверим правильность расчетов, используя взаимосвязи индексов.
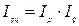 = 1,111 × 0,989 = 1,099.
= 1,111 × 0,989 = 1,099.
Вычислим индивидуальные индексы цен в мае по сравнению с апрелем:
Яблоко: ip =2501,65: 2349,56=1,065
Говядина: ip = 2299,85: 2200 = 1,045;
Баранина: ip = 3000,56: 2742,64 = 1,094;
Определим сводный индекс цен.
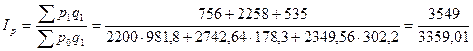 = 1,057 = 105,7%.
= 1,057 = 105,7%.
Определим сводный индекс товарооборота.
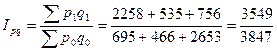 =0,923= 92,3%.
=0,923= 92,3%.
Определим сводный индекс физического объема проданных товаров.
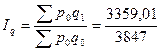 = 0,873 = 87,3%.
= 0,873 = 87,3%.
Вычислим сводный индекс цен в среднегармонической форме.
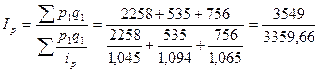 = 1,056 = 105,6%.
= 1,056 = 105,6%.
Проверим правильность расчетов, используя взаимосвязи индексов.
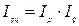 = 0,873 × 1,056 = 0,923.
= 0,873 × 1,056 = 0,923.
Вычислим сводные базисные индексы цен с постоянными весами.
Определим сводный индекс цен за февраль.
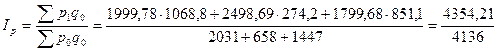 = 1,053 = 105,3%.
= 1,053 = 105,3%.
Определим сводный индекс цен за март.
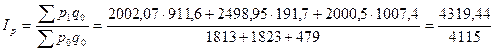 = 1,049 = 104,9%.
= 1,049 = 104,9%.
Определим сводный индекс цен за апрель.
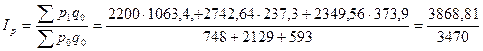 =
=
= 1,115 = 111,5%.
Определим сводный индекс цен за май.
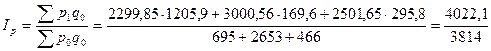 =
=
= 1,055 = 105,5%.
Вычислим сводные базисные индексы цен с переменными весами.
Определим сводный индекс цен за февраль.
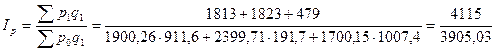 = 1,054 = 105,4%.
= 1,054 = 105,4%.
Определим сводный индекс цен за март.
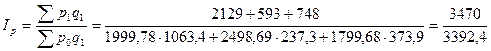 = 1,023 = 102,3%.
= 1,023 = 102,3%.
Определим сводный индекс цен за апрель.
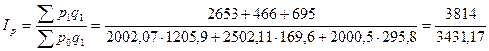 =
=
= 1,116= 111,6%.
Определим сводный индекс цен за май.
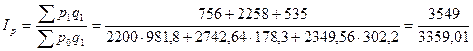 = 1,057 = 105,7%.
= 1,057 = 105,7%.
Задача 10.
На основе выборочного метода из 30 предприятий Вашего варианта произведите отбор 10 предприятий, укажите способ отбора и рассчитайте по отобранным предприятиям:
1) среднюю стоимость промышленно-производственных основных фондов;
2) предельную ошибку этой средней и пределы, в которых можно полагать генеральную среднюю с вероятностью 0,954;
3) генеральную среднюю;
4) сравните результаты расчетов, полученных в пункте 1,2,3 и сформулируйте выводы.
Решение: Произведем отбор 10 предприятий и вычислим среднюю стоимость промышленно-производственных основных фондов, дисперсию и среднее квадратичное отклонение.
Составим вспомогательную таблицу.
| № п/п | Стоимость ОПФ, xi | (x – 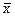 )2 )2
|
| 1,1 | 4,5369 | |
| 1,4 | 3,3489 | |
| 1,6 | 2,6569 | |
| 2,8 | 0,1849 | |
| 3,3 | 0,0049 | |
| 4,1 | 0,7569 | |
| 4,2 | 0,9409 | |
| 4,5 | 1,6129 | |
| 4,6 | 1,8769 | |
| 4,7 | 2,1609 | |
| Итого | 32,3 | 18,081 |
Получим: 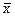 = 32,3: 10 = 3,23 млн. р.
= 32,3: 10 = 3,23 млн. р.
Dв = 18,081: 10» 1,8.
Вычислим среднее квадратичное отклонение:
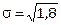 = 1,34.
= 1,34.
Определим с вероятностью 0,954 предельную ошибку средней.
Используем для этого формулу: 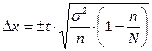 , где σ – среднее квадратичное отклонение, n – объем выборки,
, где σ – среднее квадратичное отклонение, n – объем выборки, 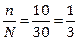 . Значение t найдем по таблице значений функции Лапласа. Для вероятности 0,954 значение t составляет 2.
. Значение t найдем по таблице значений функции Лапласа. Для вероятности 0,954 значение t составляет 2.
Получаем: 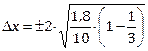 = 0,69.
= 0,69.
Запишем пределы для генеральной средней.
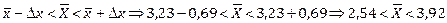
Точечной оценкой генеральной средней является выборочная средняя, т.е.
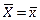 = 3,23 млн. р.
= 3,23 млн. р.
Таким образом, с вероятностью 0,954 можно утверждать, что средняя стоимость промышленно-производственных основных фондов в генеральной совокупности находится в пределах от 2,54 млн. р. до 3,92 млн. р.
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 270; Нарушение авторских прав?; Мы поможем в написании вашей работы!