Комбинаторика. Размещения. Перестановки. Сочетания

Теория вероятностей и математическая статистика

Методические указания

и контрольные задания для студентов 2 курса

заочной формы обучения всех специальностей

и направлений

(2-й семестр)

Пермь 2012 г.

Теория вероятностей и математическая статистика: Методические указания и задания для контрольной работы по теме “Теория вероятностей и математическая статистика”, для всех специализаций и форм обучения. - Пермь: Пермский институт(филиал)

Настоящие методические указания и контрольные задания составлены на основе требований государственного стандарта по дисциплине “Теория вероятностей и математическая статистика” для специальности.

Методические указания и контрольные задания подготовил:

Козлов В.В. - д.т.н., профессор, профессор кафедры

Обсуждены и одобрены на заседании кафедры от ________ ______ года, рекомендованы в качестве методических указаний, протокол № ___.

В контрольной работе каждый студент решает пять задач.

В задании 5 тем. По каждой теме студент выбирает по одной задаче: номер задачи определяется последней цифрой зачетной книжки студента

Соединения - различные подмножества множества X = {x₁, x₂,..., x_n}, содержащие m элементов, причем 1 £ m £ n.

Размещения из m элементов по n - это соединения, содержащие каждое по m элементов из n элементов множества Х, которые отличаются либо самими элементами, либо их порядком.

Число всевозможных размещений из n элементов по m в каждом равно:

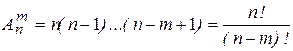, где n! = 1'2'3... (n -1) ' n.

Например, имеется 6 учебных дисциплин, в расписании стоит 4 пары занятий в день. Число вариантов расписания на день 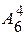=6*5*4*3=360.

Перестановки - это соединения, каждое из которых содержит n элементов и которые отличаются друг от друга только порядком элементов, т.е. это размещения из n элементов по n.

Число перестановок из n элементов равно P_n = n!.

Сочетания из n элементов множества Х по m - это соединения, которые отличаются по крайней мере одним элементом. Т.е. подмножества из m элементов множества n элементов, порядок которых не играет роли (различия в порядке элементов не меняют подмножества).

Число сочетаний из n элементов по m (n V m) в каждом равно:

.

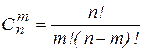Дата добавления: 2014-12-24