Рекурсивна функція і рекурсивна процедура

Вправи

Питання для роздумів

Перевірка складної умови, перевірка складної комбінації простих умов, декларативний стиль програмування, процедурний стиль програмування, сортування чисел, перестановка, число перестановок.

1. Яке найменше і найбільше число порівнянь буде виконано декларативною програмою сортування чотирьох чисел (аналогічній програмі коду 3.1 чи 3.2)? А декларативною програмою сортування восьми чисел? (Відповідь: 3 і 69 порівнянь для 4 чисел; 7 і 261233 порівнянь для 8 чисел.)
2. Яке число порівнянь буде виконано процедурною програмою сортування чотирьох чисел (аналогічній програмі коду 3.3 чи 3.4)? А сортування восьми чисел? (Відповідь: 4 порівняння для 4 чисел і 10 порівнянь для 8 чисел.)

1. Складіть процедурну програму порівняння чотирьох величин з метою їхнього сортування, взявши за зразок код 3.3.
2. Скоротіть число рядків у програмі попередньої вправи, використовуючи ключове слово ElseIf (зразок — код 3.4).
3. Створіть невеликий проект у середовищі Visual Basic для перевірки працездатності Вашого розв'язку вправ 1 і 2.

Прикметник рекурсивний найчастіше відносять до деяких об'єктів з області математики чи близьких до неї наук (у тому числі інформатики). Коротше кажучи, об'єкт рекурсивний, якщо він визначається через самого себе.

В інформатиці і програмуванні рекурсивні об'єкти зустрічаються досить часто. Ви з ними вже зіштовхнулися: це арифметичні і логічні вирази. А тут ми розглянемо інший різновид таких об'єктів — рекурсивні функції і процедури.

Рекурсивні функції і процедури дуже популярні в сучасних мовах програмування. З їхньою допомогою програмування багатьох задач, що спочатку здається важкою справою, виявляється простим і витонченим.

Що ж таке рекурсивний об'єкт (зокрема, рекурсивна функція і рекурсивна процедура)? Спробуємо більш точно розібратися в цих непростих поняттях.

Об'єкт називається рекурсивним об'єктом, якщо він цілком чи частково визначається через самого себе.

Приклад рекурсивного об'єкта, що цілком визначається через самого себе, — це загальновідома епітафія, що записав деякий піп на пам'ятнику своєму собаці (Згадайте: «У попа був собака, він її любив, вона з'їла шматок м'яса, він її убив. І в землю закопав, і пам'ятник поставив, і напис написав, що в попа був собака, він її любив, вона з'їла шматок м'яса, він її убив. І в землю закопав,... і т.д. до нескінченності».).

Об'єкти, що визначаються через себе, практичного інтересу не представляють, тому що є нескінченними. Їх приводять як забавний курйоз, на зразок згаданої епітафії.

Але об'єкти, що визначаються через себе частково, використовуються і на практиці. Яскравий приклад — визначення факторіала натурального числа в математиці.

Факторіалом натурального числа N називається така функція, що повертає добуток усіх натуральних чисел від одиниці до даного числа. Крім того, умовно вважається, що факторіалом нуля є одиниця.

Позначимо (Звичайно для позначення факторіала числа N використовується знак оклику: N!. Але тут ми не хочемо, щоб виникла плутанина, тому що за допомогою N! ми позначаємо змінну типу Single.) цю функцію так: Фaкmopіaл(N). Приклади значень факторіала: Факторіал(0)=1; Факторіал(3)=6; Факторіал(6)=720.

Факторіал числа можна визначити через сам факторіал: якщо N дорівнює нулю, то Фaкmopіaл(N) дорівнює одиниці; якщо ж N більше нуля, то Фaкmopіaл(N) дорівнює числу N, помноженому на Факторіал(N-І).

Чому факторіал лише частково визначається через самого себе? Відповідь така: факторіал числа визначається через факторіал меншого на одиницю числа. Тому процес «повторного визначення рано чи пізно закінчиться.

Формально визначення рекурсивних функцій і процедур нічим не відрізняються від описаних визначень звичайних (нерекурсивних) функцій і процедур. Щоб не повторюватися, зараз ми будемо говорити тільки про функції, але все це повною мірою буде відноситися і до процедур.

Між першим і останнім рядками визначення функції розміщаються ВиконуваніОператори. Серед них може бути й оператор виклику самої обумовленої функції. Виконання цього оператора називається рекурсивним викликом чи просто рекурсією.

Рекурсивна функція (процедура) — це така функція (процедура), серед ВиконуванихОператорів, якою є оператор виклику самої цієї функції (процедури).

Якби при роботі рекурсивної функції рекурсивні виклики виконувалися без всяких умов, її робота ніколи б не закінчилася. Тому серед ВиконуванихОператорі обов'язково повинна бути умова завершення (продовження) рекурсії.

Послідовність рекурсивних викликів називається рекурсивним спуском. Номер рекурсивного виклику в цій послідовності називається глибиною рекурсії.

Серед ВиконуванихОператорів у визначенні функції можуть бути такі, котрі виконують деяку дію і які розташовані до оператора рекурсивного виклику. Вони виконуються в тому порядку, у якому відбуваються рекурсивні виклики. Говорять, що дія виконується на рекурсивному спуску.

Серед ВиконуванихОператорів у визначенні функції можуть бути і такі, котрі теж виконують деяку дію і які розташовані після оператора рекурсивного виклику. Вони виконуються в порядку, зворотному тому, у якому відбуваються рекурсивні виклики. Говорять, що дія виконується на рекурсивному підйомі.

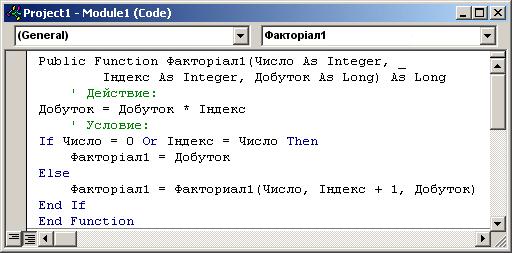
Приклад 3.2. Приведемо визначення двох рекурсивних функцій Факторіал 1 і Факторіал 2, кожна з яких повертає факторіал даного числа.

У першій з них дія виконується на рекурсивному спуску, а в другій - на рекурсивному підйомі.

Код 3.5

Функція Факторіал 1 є функцією трьох аргументів. Крім натурального Числа, факторіал якого вона повертає, у неї є ще два аргументи: Індекс і Добуток. Їхні початкові значення дорівнюють одиниці.

У ході рекурсивного спуска Індекс щораз збільшується (іноді для простоти замість того, щоб говорити: «Значення змінної А дорівнює значенню змінної Б», ми будемо говорити: «А дорівнює Б») на одиницю, а Добутку привласнюється значення, рівне добутку його старого значення на Індекс.

Під час останнього рекурсивного виклику, коли Індекс стане рівним Числу, Добуток стане рівним факторіалу цього Числа. На рекурсивному підйомі робити вже нічого не треба.

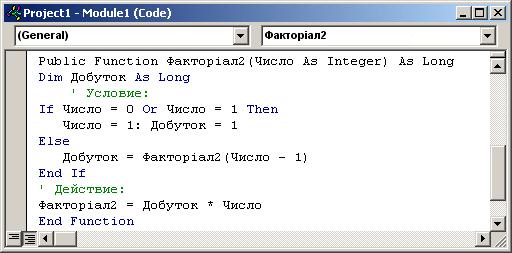
Код 3.6

Функція Факторіал 2 — це функція всього одного аргументу, — Числа. При кожному рекурсивному виклику Число зменшується на одиницю і ніяке множення при цьому не робиться. І тільки після останнього рекурсивного виклику, коли Число стане рівним одиниці, почне робитися послідовне множення на рекурсивному підйомі:

1*1 -> 1*2 -> 2*3 -> 6*4 ->...

По швидкодії і по обсягу оперативної пам'яті комп'ютера, який вимагає виконання кожної з цих функцій, вони приблизно рівні.

Hові поняття:

Дата добавления: 2014-12-23