Исследовать устойчивость разностной схемы Рунге-Кутта 2 порядка. Доказать теорему сходимости разностной схемы

Теорема. Пусть исходная задача z(u)=0 пост. корректно и разн.сх. L_h(y)=0 аппроксимирует разн.сх. с п-ом ψ_h(u)=O(h^p): lim ψ_h(u)=0 (h->0)/ и пусть разн.сх. устойчива, тогда разн.сх. сх-ся, т.е. сущ-ет lim |y_h-u_h| =0 (h->0). Причем сх-ся с порядком равным порядку погрешности аппроксимации (u – точное решение исх.з.Коши, y – точное решение разн.сх.) z_h = |y_h-u_h| = O(h^p)

Док-во. y_h = z_h + u_h подставим в разн.сх.м.Эйлера: (z_k+1 – z_k)/h = f(t_k, u_k + z_k) - (u_k+1 – u_k)/h

f(t_k, u_k + z_k) = f(t_k, u_k) + f(t_k, u_k + θz_k) z_k

(z_k+1 – z_k)/h = f(t_k, u_k) - (u_k+1 – u_k)/h + α(t_k, u_k) z_k

(z_k+1 – z_k)/h = α(t_k, z_k) + ψ_h(u­_k), y₀-u₀=z₀, k=0,.., n-1, t_k ∈ ω_n

(z_k+1 – z_k)/h = -λ z_k +| ψ_h|

|z_k+1| ≤ |1-λh| | z_k| + h| ψ_h(u­_k)|, т.к. исслед.ист и нашли, что усл.уст-ти: h ≤ 2/λ, | f_h(t_k, u_k + z_k)| ≤ λ и на осн.леммы, что пр.часть уст.: | z_k| ≤ h| ψ_h(u­₀)| + h| ψ_h(u­₁)| + … + h| ψ_h(u­_n-1)|

Т.к. y₀ = u₀: | z_k| ≤ (*)

| z_k| ≤ - из усл.теоремы об уст-ти: т.к. аппрокс. порядка р, то сущ-ет lim |z_h|=0 (h->0), |z_k|>O(h^p). в сл.разн.сх.Эйлера р=1.

Замечание: 1. Из сх=ти разн.сх. => что мы можем получить решение с любой наперед заданной точностью. Она будет достигнута соответственным дроблением сетки аргументов.

2. Из получения оценки погрешности (*) следует, что погр-ть носит суммарный или глобальный характер. Поэтому z_k будем рассм-ть как глоб.погр-ть.

z_h = y_h – u_h, y_h – точное решение, u_h – точное решение на сетке аргументов. Тогда используем: (y_k+1 – y_k)/h = f(t_k + h/2, y_k + (h/2)f(t_k, y_k)). Замена: y_h = z_h + u_h, тогда (z_k+1 – z_k)/h = f(t_k + h/2, z_k + u_k + (h/2)f(t_k, z_k + u_k)).

Приведем уравнение к удобному виду для исследования устойчивости по лин.модели

а) f(t_k, z_k + u_k) представим по ф-ле Лагранжа:

f(t_k, z_k + u_k) = f(t_k, u_k) + f_u(t_k, u_k + θ₁z_k)z_k = /* f_u(t_k, u_k + θ₁z_k) = β_k */ = f(t_k, u_k) + β_k z_k

б) f(t_k + h/2, u_k + (h/2)f(t_k, u_k) + z_k + (h/2)β_k z_k) = /* u_k + (h/2)f(t_k, u_k) = ũ_k, z_k + (h/2)β_k z_k = ž_k */ = f(t_k + h/2, ũ_k + ž_k)

Представим эту функцию по ф-ле Лагранжа:

f(t_k + h/2, ũ_k) + f_u(t + h/2_k, ũ_k + θ₂ ž_k) ž_k

(z_k+1 – z_k)/h = f(t_k + h/2, u_k + (h/2)f(t_k, u_k)) – (u_k+1 – u_k)/h + γ_k(1 + (h/2) β_k)z_k = γ_k(1 + (h/2) β_k)z_k + ψ_h(u_k), т.о., если мы заменим | γ_k | ≤ λ, | β_k | ≤ λ и будем иметь в виду, что γ_k, β_k ≤ 0, то мы образуем линейную модель разностной схемы в виде:

z_k+1 = (1 + γ_kh(1 + (h/2) β_k))z_k + hψ_h(u_k) – заменим лин.моделью

z_k+1 = (1 - λh(1 - (h/2) λ))z_k + hψ_h(u_k) – модельная задача для исследования устойчивости

|z_k| ≤ |z₀| + M₂max| ψ_h(u_j)|, (0≤j≤N-1).

Чтобы получить уст-ть по нач.данным при М=1 и, след-но, уст-ть по правой части, сделаем

|1 – λh(1 – λh/2)| ≤ 1

В случае – λh(1 – λh/2) < 0 взять др.часть нер-ва в опр. абс.величины: 1 – λh/2 ≥0 => h ≤ 2/λ

Метод Рунге-Кутта 2-го порядка обладает условной уст-тью. По теореме (из аппр. 2-го порядка и из уст-ти => сх-ть разностной схемы)

Сущ-ет lim z_h=0, h->0, если z₀=0, z₀=y₀ – u₀.

Т.о., доказана корр-ть разностного метода Рунге-Кутта 2-го порядка.

Пример. Построить разностную схему метода Рунге-Кутта 2-го порядка, определив параметр а, при котором имеет место сходимость для задачи Коши. Точность решения ε=0,001.

u’(x) = x² – au²(x), u(0) = 0, 0<x≤1.

.

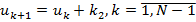
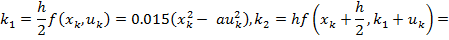
В нашем случае .

u' = f(x, y) = x² – au²(x)

|f_u(x, y)| ≤ λ => |-2au| ≤ λ

u ≤ ||u||

λ = 2a||u||

h ≤ 2/λ, h = 0.03 =>

0.03 ≤ 2/(2|a| ||u||)

|a| ≤ 1/ (0.03||u||) – a, при которых имеет место сх-ть з.Коши

6. Многошаговые методы решения задачи коши характеризуются тем, что решение в текущем виде зависит от данных не в одном предыдущем узле, а в нескольких.

Задача коши для скалярного уравнения

- Формула Ньютона-Котеса, интегрального типа, с постоянным расстоянием между узлами.

Определение. Разностная схема (*) называется m – шаговой разностной схемой Адамса. Если , то она явная; если 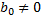, то неявная.

Особенности:

1)Для получения следующего значения надо решить нелинейную задачу:

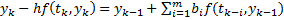– неявная разносная схема.

2) До решения методом Адамса надо знать – приближенные значения решения в к-ой точке.

3)Необходимо знать функцию в m первых точках

Дальше, при надо к каждому следующему прибавлять только 1 предыдущий: .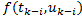

Построить такую схему, значит найти коэффициенты в известном условии аппроксимации, а потом исследовать устойчивость, и если она окажется условной то найти необходимое условие.

Двухшаговый метод Адамса(явный).

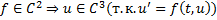. Предположим, что Погрешность аппроксимации на точках решений = невязке разносной схемы на точном решении, т.е. 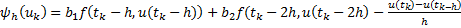по формуле Тейлора: . Надо получить 2 порядка малости по 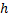. Следовательно,

таким образом

она аппроксимирует исходную задачу: возьмем

.

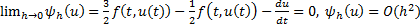Задача.

- точное решение разностной схемы.

X(t) – точное решение исходной задачи Коши.

- по формуле Лагранжа. Тогда исход задачи Коши: 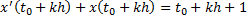. А разностная схема, тогда должна выглядеть так при подстановке в нее.

У нас 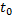по условию =0, таким образом разностная схема аппроксимирует исходную задачи коши с , то есть с первым порядком точности.

Дата добавления: 2014-12-23