Разностный метод решения интегрального уравнения Фредгольма 2-го рода

15.

Привести постановку линейной и нелинейной краевой задачи для ОДУ 2 порядка. Провести построение метода сведение к решению задачи Коши (метод пристрелки).

Дана линейная краевая задача:

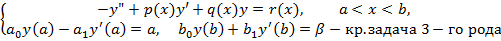(6)

Могут быть также кр. Усл. 1-го и 2-го рода:1) ; 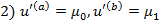, но случай с усл. 3-го рода – общий.

Для применения метода пристрелки, сделаем замену переменных:

В результате получим систему вида:

(7)

Общее решение системы ОДУ в (7) представим.

(x)

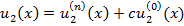(2)

Для применения метода Руне-Кутты, соответствующие задачи Кошипредставим в виде задач для системы ОДУ первого порядка:

Неоднородной:

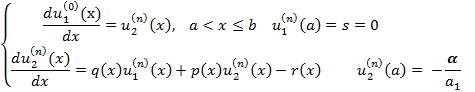
Для однородной задачи r(x)=α= 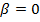получим:

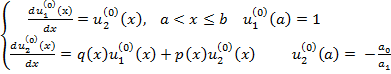(9)

Чтобы (2)было решением (6) выберем с из краевого условия для точки x=b в (6). По найденному 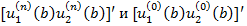получим

(10)

Решение исходной краевой задачи находим, подставляя

Пример: решить методом пристрелки: y’’+98.1siny=0, y’(0)=0, y (1)= .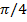

Делаем замену . Краевые условия запишем в виде:

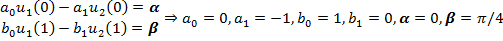. Тогда нам нужно решить две задачи Коши:

неоднородная задача:

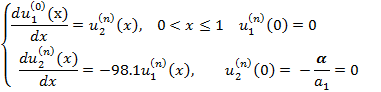
однородная:

Замечание: уравнения однородны и в первом и во втором случаях, разл. только нач. усл.

Решение будем произв, например, методом Р.-К. 4-го порядка точности:

Представив системы в векторном виде применяем формулы метода Р.-К.

,

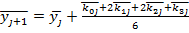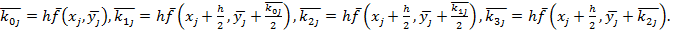
После тог, как алгоритм Р.-К. отработал мы получим 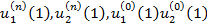. Тогда . И, наконец,

16. Дано ЛИУФ-2. Провести построение численного метода квадратур приближенного решения. В чем состоит интерполирование по ядру?

Пример: Используя квадратурную формулу трапеций, построить алг метода квадратур для решения с точностью интегрального уравнения

Числ мет реш ИУ: К ЛИУ относится ур-е Фредгольма 2 рода Ур-е им ед решенеие в том случае, если 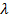не является СЗ ядра К. а,b, 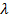, f(x), u(x) – входные данные

- если есть реш ≠ 0, то пар-ры 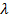явл СЗ ядра

Метод квадратур:

Числ метод прибл реш ИУФ, ИУВ основан на замене интеграла формулами числ интегрирования

,

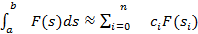– погрешность числ интегрирования. Коэфф с образуется из величин, зависящих от шага (коэф кв формулы), S- узлы кв формулы.

Распростран. явл.формулы Ньютона-Котеса(где h=const), к ним относятся ф-лы:

1.средн. прямоугол, кот им вид 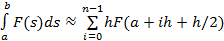, коэф 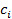=h, h=(b-a)/n,

2. Ф-ла трапеций: 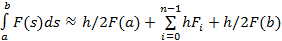, где

3.Ф-ла Симпсона:

, , если lim и не зависит от способа разбиения отрезка, то этот интеграл определенный.

Построение метода квадратур: Рассмотрим 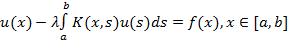. Для построения дискр модели предполагаем, что нам изв точное решение ИУ: u*(x), тогда для него запишем: u*(x)- 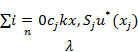=f(x)+ (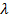, k, c, u*), F(x)=k(x.S)u(s)

Отбрасываем погрешность: (x)- 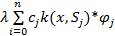*=f(x)

Получим линейные (сеточные) ур-я:

Каждое из них завясит от шага, как от пар-ра (шаг зависит от разбиения) => получили семейство сеточных ур-й (сеточная схема).

≈ u*()-прибл к точному решению.

Получили СЛАУ, кот можно решить методом Гаусса. Запишем в векторном виде:

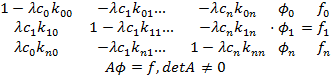
Тогда для разрешимости ур-я предполагаем, что СЗ А не совп. с СЗ ядра К, т.е. (*)

Интерполирование по ядру: Воспользуемся (*) Для построения алг: 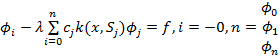. Строим: . Сначала получаем

, затем по ним получаем . Если взять и рассматривать как узлы интерполяции, то получим интерпол мнг (т.е значение ф-ии в узлах интерполяции совпадает со значением интерпол мнг)

Сеточное ур-е приближается к ЛИУФ-2, т.е имеет место устойчивость и аппроксимация.

Разностный метод решения ИУФ основан на замене интеграла функции численный интегралом: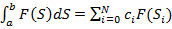

погрешность численного интегрирования.
Апроксимация:
для точного решения используем формулу

Если запишем её для сетки аргументов, то мы можем судить о погрешности апроксимаци.

Построим сеточное уравнение для погрешности:
-точное решение для дискретной задачи, -точное решение для исходной задачи на сетке

В правой части получили невязку сеточного уравнения на точном решении исходной задачи.

Определение: сеточное уравнение метода квадратур аппроксимируют ЛИУФ 2-го рода, если 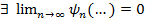и аппроксимируют его с точностью порядка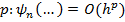

Лемма об аппроксимации: при дост. Гладкости подынтегрального выражения и при сходимости квадр. процесса равн. по ЛИФУ-2 апроксимируется сеточным уравнением с порядком сходимости квадр. формулы

Доказательство:
, если заменим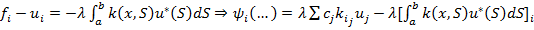

-погрешность квадратурной формулы, т.е. . При усл равн сходимостити кв процесса погрешность аппроксимирует для сеточного уравнения стремится к 0.

Устойчивость:
СЛАУ: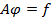

Определение: метод квадратур называют устойчивым если 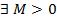, не зависимое от h и f, такое что 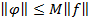или для СЛАУ:

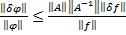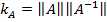, -число обусловленностити, если оно <10, то матрица хорошо обусловлена и означает непр завис реш от входных данных.

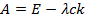, c-диаг матрица из коэффициентов квадр формулы; -матрица, полученная дискретизацией ядра

Сходимость:
Теорема:

1. λ-параметр в ИУФ-2 не является СЗ ядра 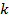. Исходная задача задана корректно.

2.Подынтегральная функции достаточно гладкая и квадрат проц сходится . При этом погрешность аппроксимации т.о. квадр метод аппроксимации исходной задачи ЛИУФ-2 с порядком использ квадр формулы.

3. Сет. Уравнение мет квадратур уст и хорошо обусл.

Тогда метод квадратур сходится в смысле:

Доказательство:

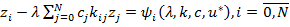-сет уравнение
, по св-ву норм

Пример. Сформировать модельное уравнение Фредгольма второго рода с ядром и точным решением . Построить для него разностную схему методом квадратур с формулой прямоугольников, обеспечивая сходимость и точность .

Общий вид ур-я: 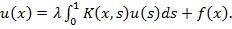Для простоты возьмем 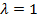(есть множество ур-й с таким решением, нам нужно всего одно).

Подставив в общий вид известные нам функции (неиз. только f(x)):

. Таким образом модельным ур-ем будет: 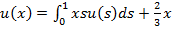. 1)Теперь постр. для него разн. схему с квадр. форм. прямоуг. (левых): , т.е. 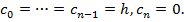2)Заметим, что формула прямоуг. имеет порядок 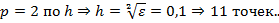3_Согласно методу мы заменим уравнения на линейные: 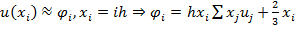– решая СЛАУ получим прибл. значения искомой функции в узлах.

Дата добавления: 2014-12-23