Теоретические сведения. В измерительной практике для уменьшения влияния случайных погрешностей на результат измерения проводят измерения с многоразовыми наблюдениями

В измерительной практике для уменьшения влияния случайных погрешностей на результат измерения проводят измерения с многоразовыми наблюдениями, а затем статистически обрабатывают полученные результаты. При этом могут быть использованы различные процедуры обработки.

Равноточными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях.

Результат измерения содержит погрешность, представляющую сумму систематической составляющей D_С и случайной составляющей :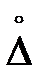

.

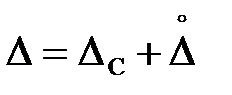Эти две составляющие погрешности резко отличаются по своим свойствам.
Их анализ, способы оценки и уменьшения - совершенно различны.

Систематическая погрешность D_С остается постоянной или изменяется по определенному закону при повторных измерениях одной и той же физической величины. Она является математическим ожиданием 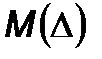погрешности D измерения

.

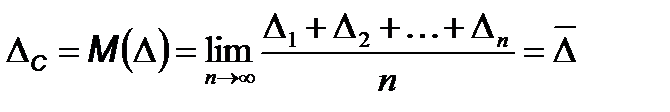Обнаружение систематической погрешности – трудоемкая операция и может быть выполнена несколькими способами:

1) Проверка данного измерительного прибора с помощью образцового (более точного). При измерении одной и той же физической величины измерительным и образцовым приборами получают разные показания: X _раб и X _обр. Их разность является абсолютной систематической погрешностью прибора:

.

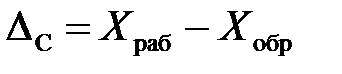Тогда показания рабочего прибора корректируются введением поправки П, численно равной

.

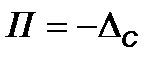При этом за результат измерения необходимо принимать величину

.

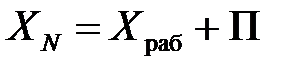2) Метод замещения. В этом случае измеряемая величина 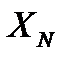заменятся известной величиной 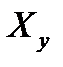таким образом, чтобы показание прибора осталось неизменным. Тогда результат измерения .

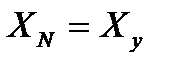3) Метод компенсации по знаку применяется при направленном действии причины, вызывающей систематическую погрешность. Выполняют измерения так, чтобы погрешность входила с разными знаками в формулы

; ,

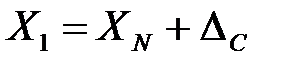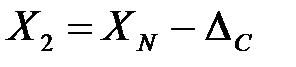тогда .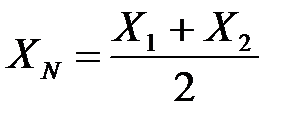

Переменные систематические погрешности разделяют на прогрессирующие и периодические. Для устранения этих составляющих необходимо найти функциональную связь погрешности и влияющего фактора и вводить поправку на основании полученных зависимостей.

Сложную задачу по выявлению и исключению систематической погрешности не всегда удается довести до конца и поэтому остается неисключенная часть систематической погрешности.

Нетрудно убедиться, что результат измерения – случайная величина.
Для этого достаточно измерить несколько раз одну и ту же физическую величину с помощью прибора, обладающего достаточно высокой чувствительностью. Результаты измерений будут в общем случае отличаться друг от друга. Это объясняется влиянием многих дестабилизирующих факторов, к которым можно отнести: тепловой шум, шум электронных приборов, случайные воздействия на результат измерения коммутационных процессов в цепях, случайное изменение электромагнитных полей, температуры окружающей среды, влажности, вибрации, напряжения питания измерительного прибора и т.д. Полное совпадение результатов измерений всегда указывает на то, что чувствительность средств измерений недостаточна для того, чтобы обнаружить это явление.

Таким образом, случайная погрешность 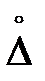изменяется нерегулярно, непредсказуемо при повторных измерениях. Она вызывается большим количеством причин, характер и размер влияния которых на измеряемую величину при единичном измерении не может быть определен. Однако путем выполнения многократных наблюдений и путем обработки результатов наблюдений статистическими методами можно дать оценку этим погрешностям. Вклад в случайную погрешность вносит случайная составляющая погрешности средства измерений.

Одной из важнейших характеристик случайной погрешности является закон распределения плотности вероятности – плотность распределения вероятносте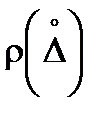й или 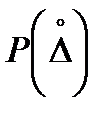– функция распределения вероятностей.

Законы распределения могут быть дискретными (для дискретных случайных величин) и непрерывными (для непрерывных величин).

Дискретный закон распределения представляет совокупность значений случайной величины 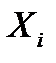и соответствующих им вероятностей 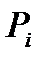. Условие нормировки закона распределения вероятностей дискретной случайной величины:

.

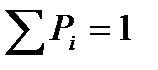Для непрерывных случайных величин с известным законом распределения 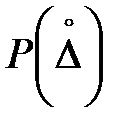вероятность того, что данная случайная величина 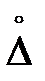примет значение в интервале от 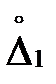до 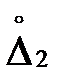, определяется площадью, ограниченной этой кривой и осью абсцисс (рис. 4.1), т.е.

.

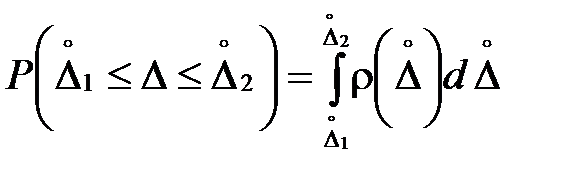Условие нормировки для непрерывной случайной величины имеет вид:

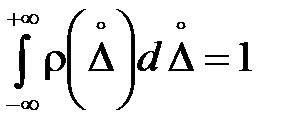
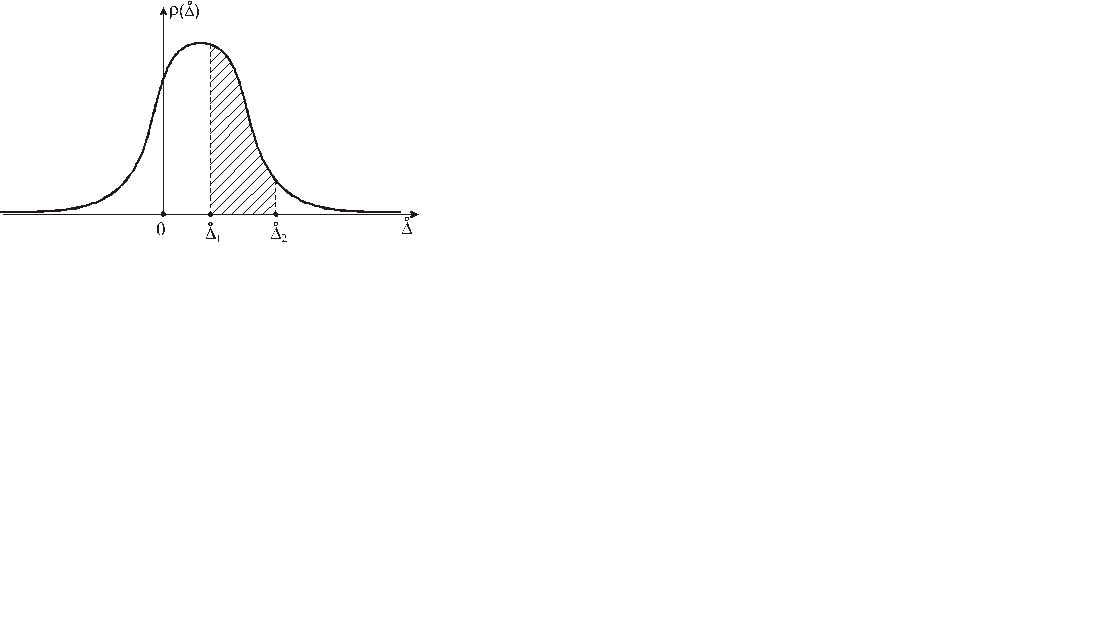
Рисунок 4.1 – Нормальный закон распределения

Если дестабилизирующих факторов, обуславливающих случайную погрешность много (3 и более), то закон распределения плотности вероятности 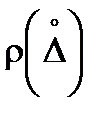будет стремиться к гауссовой кривой – нормальному закону распределения (рис. 4.2, а), описываемого соотношением:

.

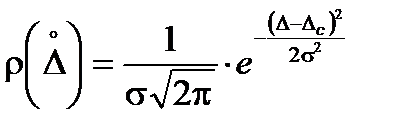Из представленного графика видно: если в состав погрешности входит систематическая составляющая 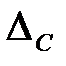, то закон распределения плотности вероятности будет смещен на эту величину. Если же систематическая погрешность исключена 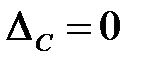(М[D] = 0), то 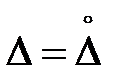и максимальное значение такой кривой Гаусса

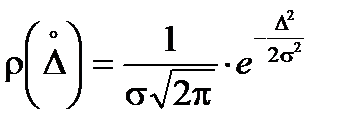
достигается при 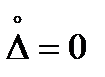(рис. 4.2.б).

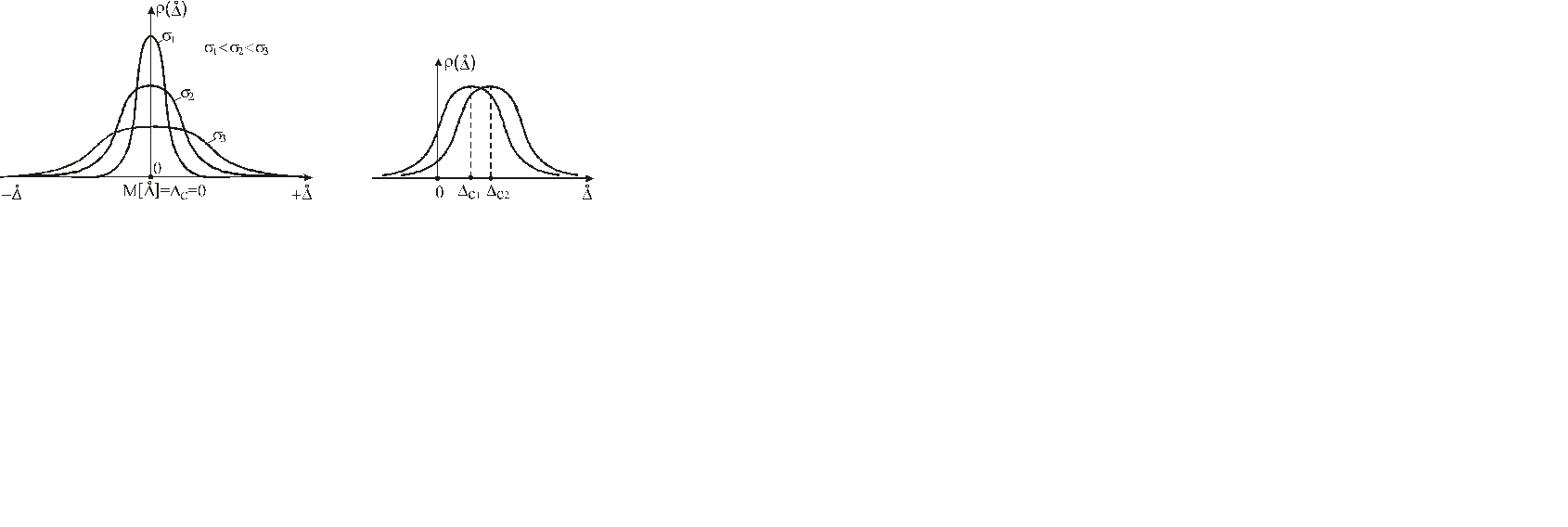
а) б)

Рисунок 4.2 – Кривые Гаусса

а) для разных значений систематической составляющей погрешности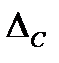

б) для разных значений среднеквадратического отклонения s.

Характер закона распределения изменяется в зависимости от параметров s и s² (рис. 4.2, б). Дисперсия

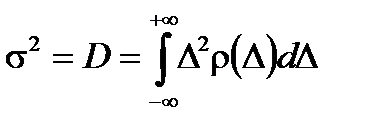
характеризует рассеяние случайной величины относительно среднего значения. Среднеквадратическое значения отклонения (СКО)

.

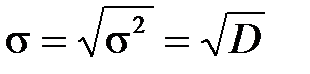Дисперсия и СКО характеризуют точность измерений. Чем больше s² и s, тем меньше точность, т.е. больше погрешность измрений.

При нормальном законе распределения с 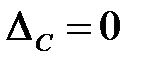вероятность появления случайной погрешности в интервале от –D_гр до +D_гр определяется выражением

.

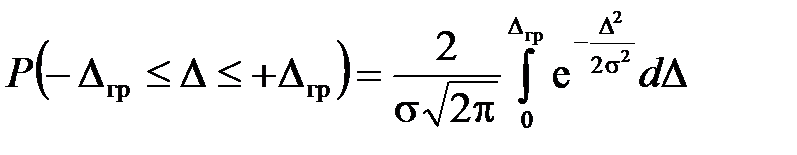При введении нормированной случайной переменной 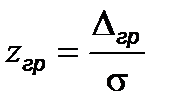выражение P (D) преобразуется к виду:

,

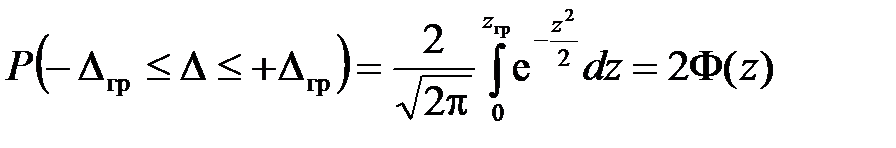где Ф(z) – интеграл вероятности.

Доверительная вероятность P _дов при заданных граничных значениях погрешности – это вероятность нахождения случайной величины внутри доверительного интервала D_дов (доверительных границ). Доверительная вероятность определяется площадью под кривой (на рис. 4.3 заштрихованная область).

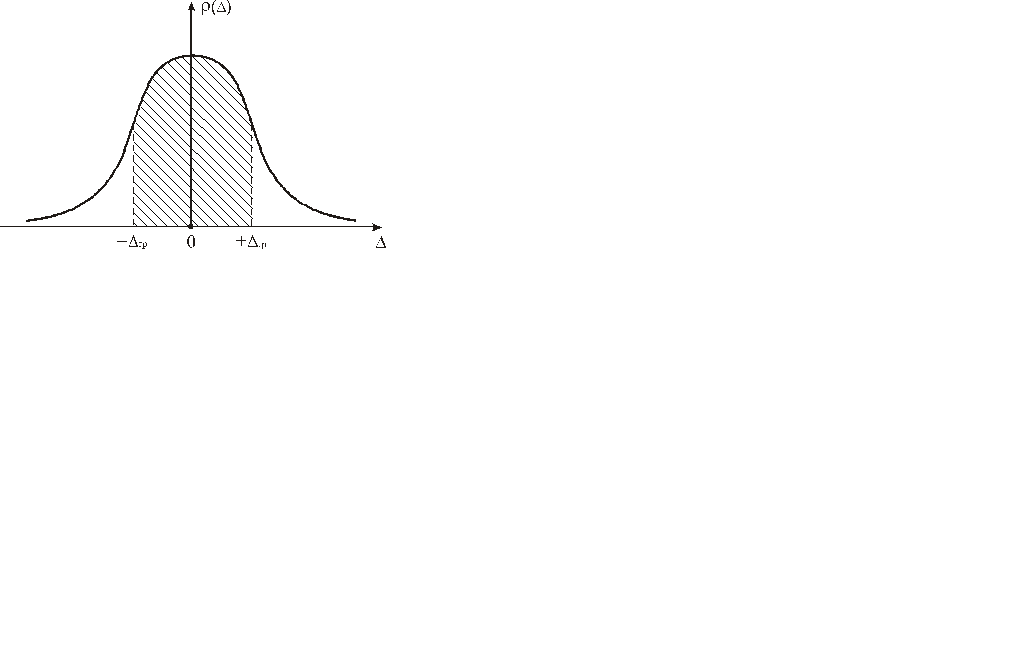
Рисунок 4.3 – Доверительная вероятность при заданных граничных значениях погрешности

Функция Ф(z) табулирована или определяется по графику (рис. 4.4).

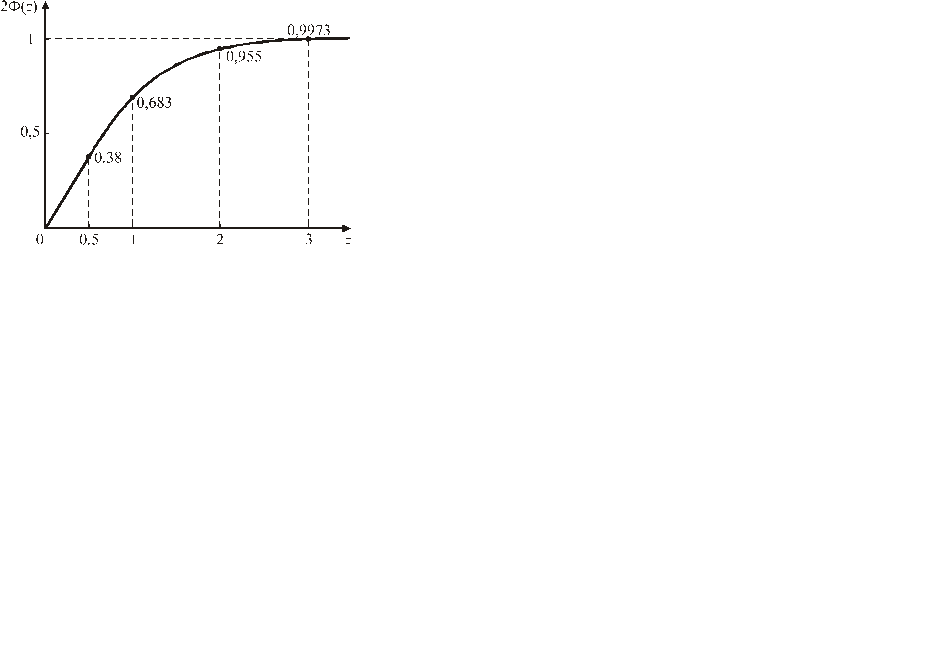
Рисунок 4.4 – Функция Лапласа для разных значений нормированной переменной

Если задана P _дов, то по графику или таблице находят z _гр, затем определяют D_гр = z _гр×s. Доверительный интервал D_дов = –D_гр … +D_гр, он с заданной вероятностью накрывает истинное значение 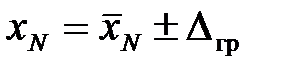, Р _дов = …

В зависимости от целей измерений доверительную вероятность на практике устанавливают Р _дов = 0,95 … 0,99.

За максимальное значение погрешности, описываемой нормальным законом распределения 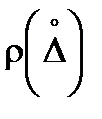, принимают интервал D_max = ±3s, что соответствует вероятности появления в нем погрешности с Р _дов = 0,9973.

Вероятность того, что погрешность превысит максимальное значение, определяется выражением:

,

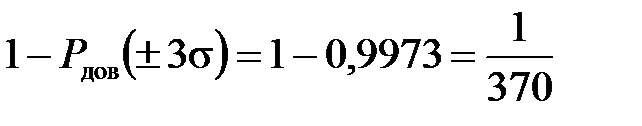означающим, что погрешность в 369 случаях из 370 попадает в интервал ±3s и лишь в одном случае выходит за эти пределы.

Дата добавления: 2014-12-24