
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Порядок выполнения работы. Энтропийное значение погрешности, представленное гистограммой распределения
|
|
|
|
Энтропийное значение погрешности, представленное гистограммой распределения
Если на основе ограниченного числа измерений была построена ступенчатая гистограмма, то, найдя ее энтропию, можно затем заменить гистограмму законом распределения выбранной формы (равномерным, нормальным) и определить энтропийный интервал погрешности.
Пусть гистограмма состоит из m столбов.
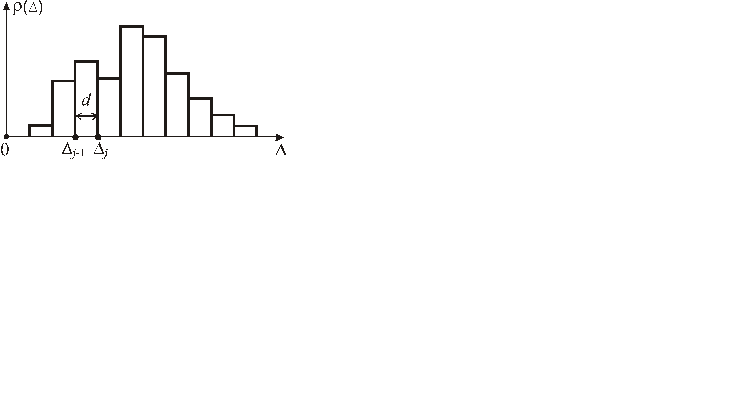
| Высота столбца: 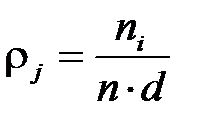 ,
где j = 1, 2, …, m – количество интервалов;
n –число всех измерений;
ni – число измерений, попавших в j -й
интервал. ,
где j = 1, 2, …, m – количество интервалов;
n –число всех измерений;
ni – число измерений, попавших в j -й
интервал.
|
Энтропия погрешности определяется суммой энтропийных значений каждого j -го интервала:
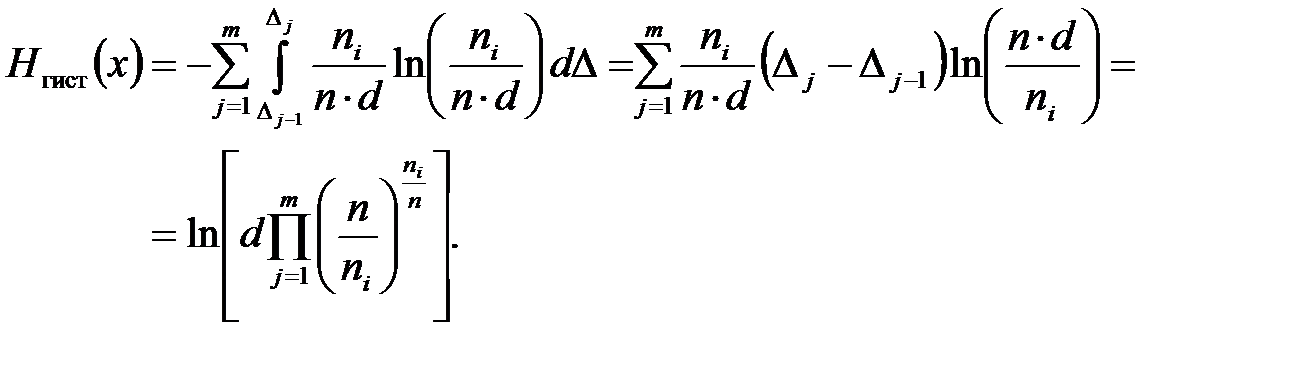
1. Измерить сопротивление n резисторов одного номинала прибором Щ 4313 в режиме омметра. Результаты наблюдений занести в табл. 4.1.
2. Предполагаем, что измеряемые значения Ri подчиняются нормальному закону распределения. Последовательность обработки результатов проводить в соответствии с методикой, изложенной в ГОСТ 8.207–76:
2.1. Вычислить среднее арифметическое значение 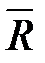 измеряемой величины
измеряемой величины 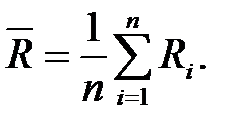
2.2. Вычислить разности между результатами отдельных наблюдений Ri и среднего значения 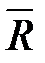 – случайное отклонение результата наблюдения
– случайное отклонение результата наблюдения 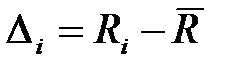 . Значение D i занести в табл. 4.1. Определить сумму всех погрешностей
. Значение D i занести в табл. 4.1. Определить сумму всех погрешностей 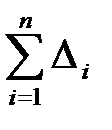 .
.
При большом числе измерений сумма случайных погрешностей стремится к нулю 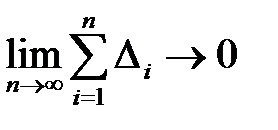 . Этот вывод основывается на аксиоме случайности теории случайных погрешностей, что при очень большом числе измерений и при отсутствии систематических DС погрешностей, положительные и отрицательные погрешности встречаются одинаково часто.
. Этот вывод основывается на аксиоме случайности теории случайных погрешностей, что при очень большом числе измерений и при отсутствии систематических DС погрешностей, положительные и отрицательные погрешности встречаются одинаково часто.
2.3. Рассчитать величины квадрата абсолютной погрешности 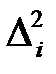 , результаты занести в табл. 4.1.
, результаты занести в табл. 4.1.
Таблица 4.1
| № | Измеренное значение Ri, Ом, кОм, МОм | Абсолютная погреш-ность измерения
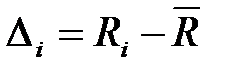
| Квадрат абсолютной погрешности
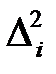 
|
| … | … | … | … |
| n | |||
Среднее арифметическое значение сопротивлений
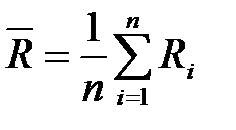
| Сумма абсолютных погрешностей
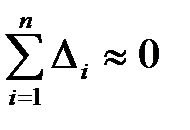
| Сумма квадратов абсолют-ных погрешностей
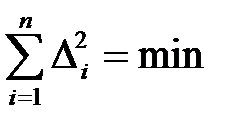
|
Сумма квадратов случайных погрешностей должна быть минимальной 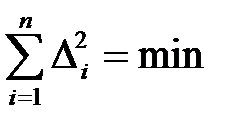 . Такой вывод основывается на аксиоме распределения, что при большом количестве измерений малые погрешности встречаются чаще, чем большие; очень большие погрешности практически не встречаются.
. Такой вывод основывается на аксиоме распределения, что при большом количестве измерений малые погрешности встречаются чаще, чем большие; очень большие погрешности практически не встречаются.
2.4. Определить оценку среднеквадратического отклонения результатов каждого из n одноразовых наблюдений 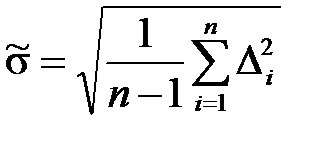 .
.
2.5. Исключить аномальные результаты (грубые промахи) по критерию «трех сигм». Для этого из ряда значений D i найти наибольшие и сравнить их с 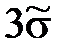 . Такой критерий надежный при числе измерений
. Такой критерий надежный при числе измерений 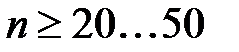 . Если
. Если 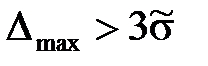 , то подозреваемый в аномальности результат Dmax исключить, а затем повторить сначала расчеты по пунктам 2.1. – 2.4.
, то подозреваемый в аномальности результат Dmax исключить, а затем повторить сначала расчеты по пунктам 2.1. – 2.4.
2.6 Найти оценку СКО среднего арифметического значения 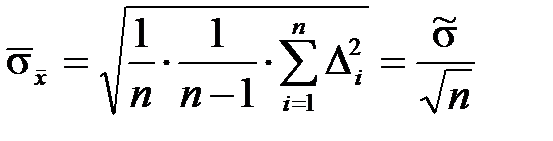 .
.
2.7. Определить доверительные границы случайной составляющей погрешности и записать результат измерений. Если за результат измерений принято среднее значение 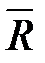 , то
, то
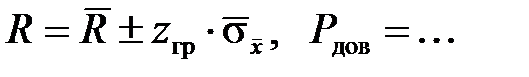
При Р дов = 0,997 z гр = 3 и 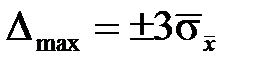 .
.
При любой другой доверительной вероятности Р дов можно воспользоваться табличным (или из графика) значением интервала вероятности Ф(z) = Р дов, по его значению можно найти z гр и далее, так как 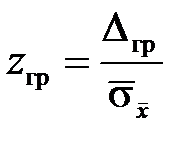 , можно определить Dгр и записать результат
, можно определить Dгр и записать результат
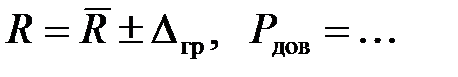
2.8. В случае, если число измерений n мало 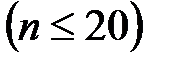 , то
, то 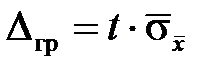 ,
,
где t – коэффициент Стьюдента, который определяют из табличных данных при заданных Р дов и количестве (n) наблюдений.
2.9. Учитывая, что систематическая погрешность DС вошла в состав результата измерений 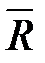 , необходимо определить доверительные границы неисключенной систематической погрешности. В качестве DС используют погрешность средства измерения
, необходимо определить доверительные границы неисключенной систематической погрешности. В качестве DС используют погрешность средства измерения
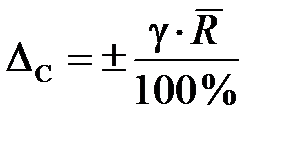 ,
,
где g – класс точности прибора, %.
Для прибора Щ 4313 относительная погрешность определяется по формуле:
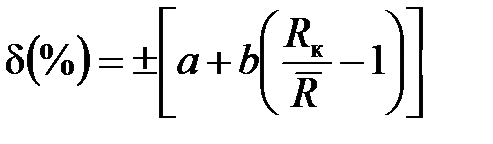 ,
,
где a и b – коэффициенты, зависящие от конечного значения шкалы R к.
Согласно паспортным данным прибора Щ4313, при R к = 500 Ом, a = b = 1,5. При R к = 5 кОм и более, a = b = 0,5.
Абсолютная погрешность: 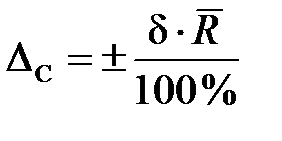 .
.
В случае, если 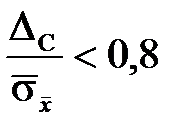 , то неисключенной систематической погрешностью пренебрегают и принимают D = Dгр; если
, то неисключенной систематической погрешностью пренебрегают и принимают D = Dгр; если 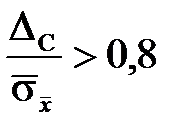 , то пренебрегают случайной погрешностью и считают, что D = DС. В случае равенства
, то пренебрегают случайной погрешностью и считают, что D = DС. В случае равенства 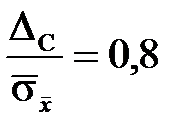 вычисляют
вычисляют  ,
, 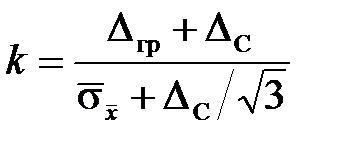 , и тогда
, и тогда 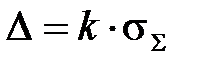 , а результат представляют в виде:
, а результат представляют в виде:
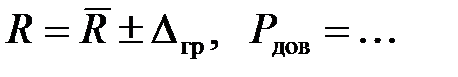
Числовое значение результата измерения должно заканчиваться цифрой того же порядка, что и значение погрешности D. При этом число значащих цифр при определении D не должно превышать двух.
3. Определить закон распределения погрешностей результатов измерений.
Для идентификации закона распределения необходимо построить
гистограмму (рис. 4.5). Для этого весь диапазон D i разбивают на m одинаковых интервалов. Значение m должно быть нечетным (m = 9 … 13).
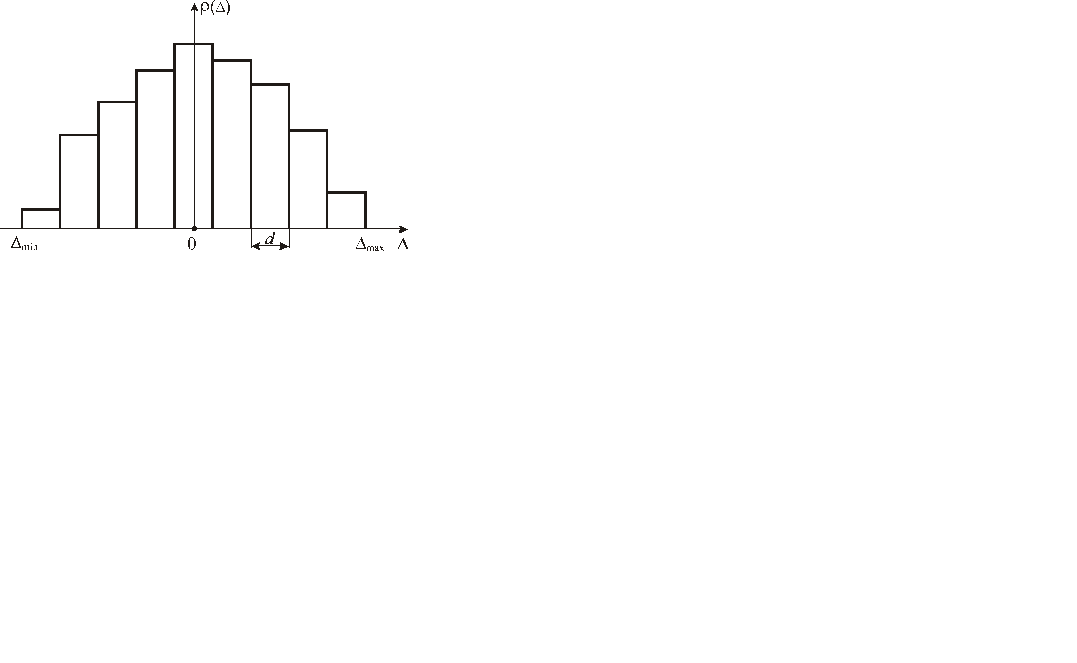
Рисунок 4.5 – Гистограмма
Ширину интервала определяют по соотношению:
 ,
,
где Dmax, Dmin – соответственно наибольшее и наименьшее значение погрешности D i; m – количество интервалов.
Затем подсчитывают вероятность нахождения случайной погрешности в j интервале
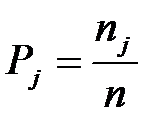 ,
,
где j – 1, 2, …, m; nj – число погрешностей, которые попадают в j -ый интервал;
n – число всех измерений.
Если погрешность попадает на границу интервала D j, то ее можно отнести либо к j -му интервалу, либо к (j +1)-му интервалу, т.е. она учитывается только один раз.
По оси результатов наблюдений откладывают интервалы D j в порядке нарастания номеров и на каждом интервале строится прямоугольник высотой 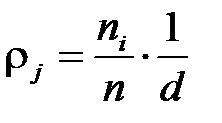 (средняя плотность в интервале D j = d).
(средняя плотность в интервале D j = d).
В этом случае площадь под гистограммой будет равна единице. Полученную гистограмму аппроксимируют кривой и делают выводы о законе распределения.
Как способ оценки близости распределения выборки экспериментальных данных к принятой аналитической модели закона распределения используется критерий согласия. Наибольшее распространение в практике получил критерий Пирсона.
3.1. Приравняв энтропию распределения, представленного гистограммой, к энтропии равномерного закона, получим энтропийное значение случайной погрешности DЭ (см. рис. 4.6). При этом равенство энтропий Н гист(D) = Н равн(D) создает одинаковое дезинформирующее действие погрешности на измеряемую величину.
Н гист(D) = Н равн(D) = ln(2DЭ).
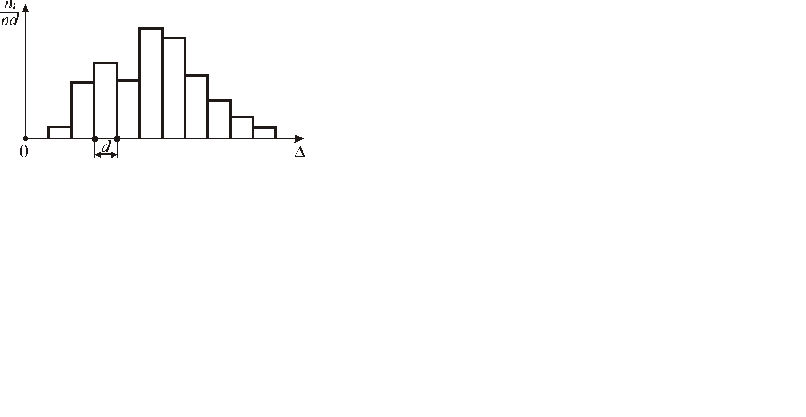
| Þ | 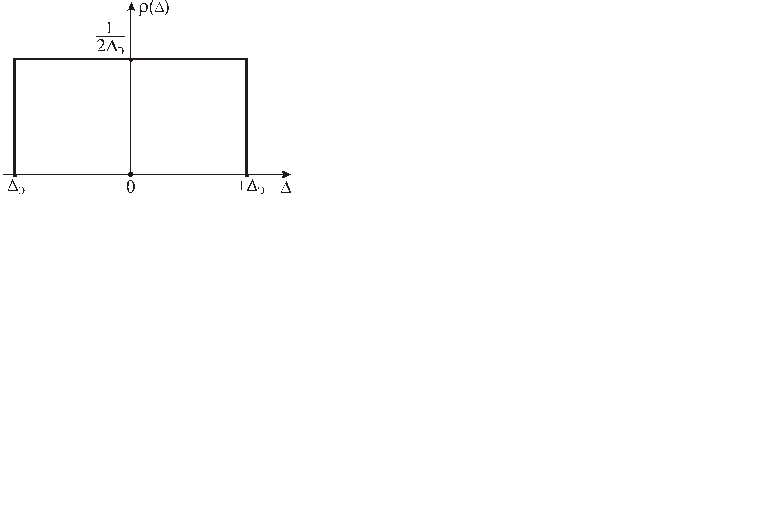
|
Рисунок 4.6 – Распределение случайной погрешности
С учетом полученного значения DЭ результат измерения сопротивления R запишем в виде:
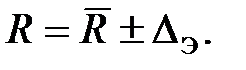
3.2. Приравняем энтропию распределения, представленного гистограммой, к энтропии нормального закона:
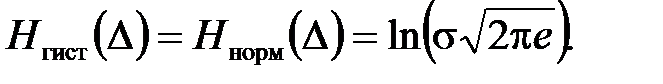
Вычислим СКО: 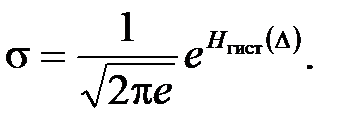
Энтропийный интервал: 
Используя рассчитанное значение s, можно построить график r(D) нормального закона распределения по известной формуле 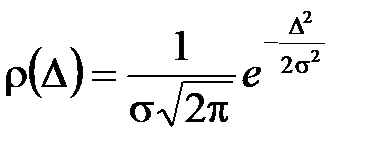 .
.
Площадь под кривой r(D) и площадь всех столбцов гистограммы должны быть одинаковыми. Для наглядности сравнения кривую r(D) нормального закона распределения необходимо совместить с рисунком гистограммы (см. рис. 4.7.).
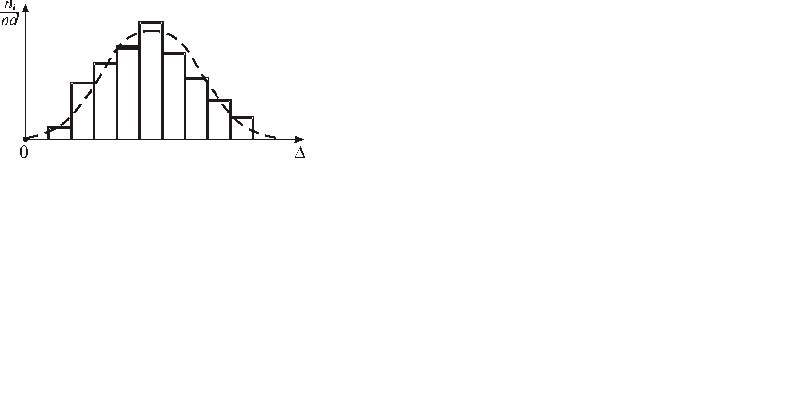
| Þ | 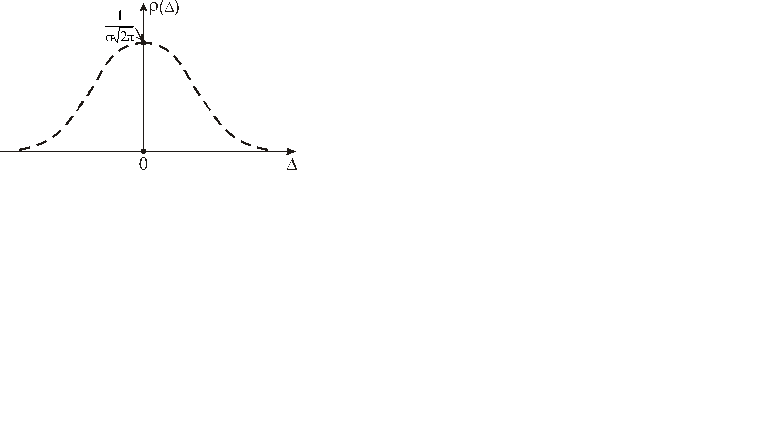
|
Рисунок 4.7 – Нормальный закон распределения случайной погрешности
4.3. Содержание отчета:
1. Цель работы.
2. Схема измерения.
3. Таблицы и графики результатов измерения.
4. Результаты обработки эксперимента.
5. Выводы и замечания по работе.
4.3. Контрольные вопросы:
1. Что такое случайная погрешность?
2. Основные законы распределения случайной погрешности.
3. Энтропийное значение погрешности.
4. Как построить гистограмму?
5. Как определить максимальную погрешность при нормальном законе распределения?
6. Дать определение среднеквадратическому значению погрешности.
СПИСОК ЛИТЕРАТУРЫ
1. Орнатский П.П. Теоретические основы информационно-измерительной техники. – К.: Вища школа, 1984 г. – 455 с.
2. Сергеев А.Г., Крохин В.В. Метрология. – М.: Логос, 2001 г. – 408 с.
3. Мейзда Ф. Электронные измерительные приборы и методы измерений. – М.: Мир, 1990 г. – 507 с.
4. Кушнир Ф.В. Электрорадиоизмерения. – Л.: Энергоатомиздат, 1986 г. – 320 с.
5. Найденов А.И., Новопольский В.А. Электронно-лучевые осциллографы. – М.: Энергоатомиздат, 1983. – 414 с.
6. Поліщук Є.С. та інш. Метрологія та вимірювальна техніка. – Львів: Бескид Біт, 2003 р. – 544 с.
7. Дорожовець М. та інш. Основи метрології та вимірювальної техніки. Т1, Т2. – Львів: Львівська політехніка, 2005 р.
8. Шпінь О.П. Прикладна метрологія. – К.: НТУУ «КПІ», 2007 р. – 256 с.
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 626; Нарушение авторских прав?; Мы поможем в написании вашей работы!