Надежность результата многократных измерений. Коэффициент Стьюдента

Доверительной вероятностью или надежностью P серии измерений называется вероятность попадания истинного значения измеряемой величины в данный интервал (выражается в долях единицы или в процентах).

Интервал (<x>±- ∆x) в который попадает истинное значение искомой величины с заданной доверительной вероятностью P(∆x), называют доверительным интервалом или интервалом надежности и для краткости обозначают как ∆x.

Чем больше доверительный интервал, тем больше доверительная вероятность того, что результат измерения попадет в него. Величина доверительного интервала, рассчитывается методами теории вероятностей и математической статистики и определяется выбором вида функции распределения случайных величин f(∆x).

Для всех функций распределения, базовым является распределение Гаусса, справедливое для большого количества равноточных измерений :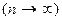

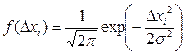[1.5]

где величина 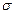называется среднеквадратичным или стандартным отклонением 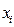от среднего значения <x> а, 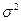дисперсией распределения.

Распределение Гаусса показывает, что вероятность появления малых случайных погрешностей больше вероятности появления больших погрешностей, при этом случайные погрешности равные по абсолютной величине, но противоположные по знаку встречаются одинаково часто.

При лабораторных измерениях (n < 20) для расчета интервала надежности используется распределение Стьюдента (при 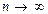распределение Стьюдента переходит в распределение Гаусса), которое позволяет по заданной величине надежности P(∆x) найти величину доверительного интервала ∆x, с помощью поправочных коэффициентов Стьюдента:

[1.6]

где 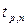- коэффициент Стьюдента, зависящий от выбора доверительной вероятности p и числа измерений n, S – среднеквадратичное отклонение – (СКО), вычисляемое по формуле:

[1.7]

Величина интервала ∆x, рассчитанная при помощи формулы [1.6] стремится к нулю при увеличении числа опытов.

Коэффициенты Стьюдента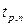

Число измерений n	Доверительная вероятность (надежность), р
0,90	0,95	0,99	0,999
	6,314	12,706	63,657	636,619
	2,920	4,303	9,925	31,598
	2,353	3,182	5,841	12,941
	2,132	2,776	4,604	8,610
	2,015	2,571	4,032	6,859
	1,943	2,447	3,707	5,959
	1,895	2,365	3,499	5,405
	1,860	2,306	3,355	5,041
	1,833	2,262	3,250	4,781

Очевидно, что число опытов имеет смысл выбрать таким, чтобы случайная погрешность среднего сравнялась с погрешностью прибора либо стала меньше ее. Дальнейшее увеличение числа измерений теряет смысл, так как не увеличит точность получаемого результата

Дата добавления: 2014-12-24