Контрольная работа №1. 1. Охотник может произвести по летящей дичи один за другим три выстрела с вероятностями попадания соответственно 0,8; 0,6 и 0,4

1. Охотник может произвести по летящей дичи один за другим три выстрела с вероятностями попадания соответственно 0,8; 0,6 и 0,4. Стрельба прекращается после попадания в цель. Найти вероятность того, что охотник:

а) попадет в дичь при третьем выстреле; б) произведет все три выстрела.

Решение:

1) Первые два выстрела - промахнулся, третий - попал, вероятность равна p = (1-0.8)*(1-0.6)*0.4 = 0.2*0.4*0.4 = 0.032

2) Первые два выстрела промахнулся, третий выстрел - не имеет значения, вероятность равна p = (1-0.8)*(1-0.6) = 0.2*0.4 = 0.08

2. В партии из 8 деталей 6 деталей – стандартные. Наугад отбираются две детали. Составить закон распределения случайной величины, равной числу стандартных деталей среди отобранных. Найти ее математическое ожидание дисперсию и функцию распределения.

Решение:

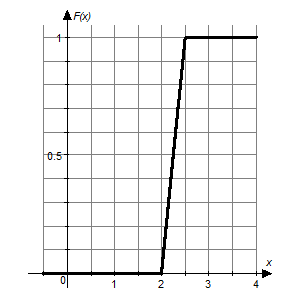
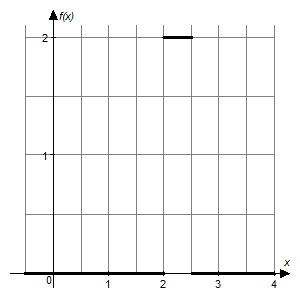
3. Плотность распределения случайной величины имеет вид:

Решение:

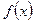Плотностью распределения вероятностей непрерывной случайной величины называют функцию – первую производную от функции распределения :

; ;

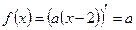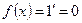
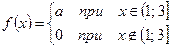
Параметр 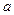найдем, исходя из условия нормировки: .

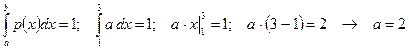
Таким образом, 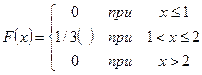и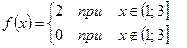

Математическое ожидание непрерывной случайной величины по определению: или .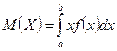

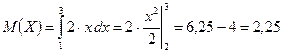
Дисперсия случайной величины проще всего может быть рассчитана по следующей формуле:

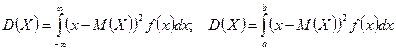
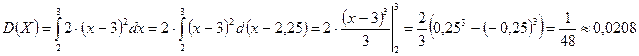
4. При въезде в новую квартиру в осветительную сеть было включено 4

новые электролампочки. Каждая электролампочка в течение года может перегореть с вероятностью 0,8. Найти вероятность того, что в течение года из числа включенных в начале года придется заменить новыми: а) не менее 3 ламп; б) не более 3 ламп.

Решение:

n = 20

p = 0.2 - вероятность, что лампочка перегорит

q = 1-p = 0.8

np = 20*(0.2) = 4

npq = 4*(0.8) = 3.2

m - количество перегоревших лампочек

A = {в течении года не менее половины лампочек придется заменить новыми}

P(A) = P(10 <= m <= 20) ~ [по интегральной формуле Муавра-Лапласа]

~ Ф((20-4)/sqrt(3.2)) - Ф((10-4)/sqrt(3.2)) =

= Ф(16/sqrt(3.2)) - Ф(6/sqrt(3.2)) ~

~ Ф(8.94) - Ф(3.35) ~

~ 0.5 - 0.49966 = 0.00034

5. Уровень воды в реке – это случайная величина со средним значением 2,5 м и стандартным отклонением 20 см. Оценить вероятность того, что в наудачу выбранный день:

а) уровень превысит 3 м; б) окажется в пределах от 2,2 м до 2,8 м.

Решение.

Обозначим через X − уровень воды в реке. Это непрерывная случайная величина, имеющая нормальное распределение с параметрам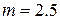и и . Поэтому вероятность попадания случайной величины в промежуток [ а, b ]вычисляется по формуле:

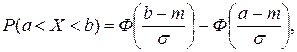
где 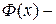функция Лапласа.

а) Вероятность того, что уровень воды превысит 3 м:

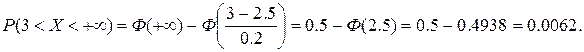
б) Вероятность того, что уровень воды окажется в пределах от 2,2 м до 2,8 м:

Ответ: а) 0,0062; б) 0,8664.

Дата добавления: 2014-12-25