Тема 2. Статистическое изучение взаимосвязи социально-экономических явлений

.

Величина равного интервала вычисляется по формуле

соответственно наибольшее и наименьшее значение

признака (расход кормов на одну голову) в совокуп­ности; п - число групп.

Для определения максимального и минимального зна­чения признака можно использовать стандартные функции МАКС() и МИН() соответственно.

Интервальный ряд распределения строится в виде групповой таб­лицы, в сказуемом которой показывается число единиц в каждой группе (частота) или их удельный вес в общей численности единиц совокупности (частость). Кумулятивный ряд — это ряд, в котором подсчитываются накопленные частоты, он показывает, сколько еди­ниц совокупности имеют значение признака не больше, чем данное значение, и вычисляется путем последовательного прибавления к час­тоте первого интервала частот последующих интервалов.

В таблице 2 приведены ряды распределения предприятий по уровню кормления коров.

Таблица 2. Интервальный и кумулятивный ряды распределения предприятий по уровню кормления коров

Группы предприятий по затратам кормов на одну корову, ц к.ед.	Число предприятий (частота)	Удельный вес предприятий в группе в общей численности, % (частость)	Накопленная частота
№	Нижняя граница группы	Верхняя граница группы
I	39,4	46,5		35%
II	46,6	53,6		40%
III	53,7	60,7		25%
ИТОГО		100%	X

Число предприятий определяется с помощью функции ЧАСТОТА (Диапазон исходных данных; Диапазон групп). Диапазон исходных данных — это столбец, содержащий группировочный признак (расход кормов на одну голо-^ВУ); Диапазон групп — столбец, содержащий верхние границы выделенных интервалов.

ЧАСТОТА — функция массива, поэтому необходимо перед вводом формулы выделить диапазон, где будет размещаться результат вычисления, заканчивать ввод нужно комбинацией клавиш Ctrl + Shift + Enter.

4. Для графического изображения интервального ряда распреде­ления применяется гистограмма частот. При построении гистограммы на оси абсцисс откладываются равные отрезки, которые в принятом масштабе соответствуют величине интервалов ряда. На отрезках пря­моугольниками с высотой в масштабе оси ординат изображают часто­ты ряда (рис. 2).

В таблице 2 выделить номера групп и число предприятий (для выделения несмежных областей необходимо удер­живать клавишу Ctrl), выбрать Вставка - Диаграмма - Гистограмма.

Рис. 2. Гистограмма частот

Расход кормов на одну голову, ц к.ед.

Рис. 3. Кумулята распределения предприятий по расходу кормов на одну голову

Для изображения кумулятивного ряда распределения использует­ся кумулятивная кривая (кумулята). Накопленные частоты наносятся на чертеж в виде ординат; соединяя вершины отдельных ординат прямыми, получают ломаную линию, которая, начиная с нуля, непре­рывно поднимается над осью абсцисс до тех пор, пока не достигает высоты, соответствующей общей сумме частот ряда (рис. 3).

5. Определение зависимости молочной продуктивности коров в сельскохозяйственных предприятиях от уровня их кормления мето­дом группировок предполагает осуществить сводку статистических данных путем суммирования значений изучаемых признаков по груп­пам и в целом по совокупности, а затем расчета средних показателей молочной продуктивности и расхода кормов на одну голову. Сводные показатели представлены в таблице 3.

Для удобства расчета сводных данных группы в отсорти­рованной таблице 1 необходимо выделить цветом. Для определения общего поголовья целесообразно ис­пользовать функцию СУММ(), валового надоя и расхода кормов — функцию СУММПРОИЗВ().

Таблица 3. Сводные показатели

Таблица 4. Средние характеристики групп

№ группы	Среднее поголо­вье коров, гол.	Расход кормов на одну корову, ц к.ед.	Среднегодовой удой молока от одной коровы, ц
I 39,4-46,5		43,19	27,20
II 46,6-53,6		50,34	35,25
III 53,7-60,7		57,46	44,83
В среднем по СОВОКУПНОСТИ		48,51	33,49

№ группы	Число пред­приятий в группе	Поголовье коров, гол.	Валовой надой, ц	Расход кор­мов, ц к. ед.
I 39,4-46,5		8 677	235 999,7	374 777,2
II 46,6-53,6		7 114	250 736,0	358 094,7
III 53,7-60,7		3 712	166 396,9	213 282,6
ИТОГО		19 503	653 132,6	946 154,5

На основе проведенной сводки данных рассчитывается таблица 4, содержащая средние характеристики анализируемой совокупности. Подлежащее аналитической таблицы — группы предприятий по уров­ню кормления, ц к. ед.; сказуемое таблицы — среднее поголовье ко­ров в группе; средние затраты кормов на одну корову, ц к.ед.; средний надой молока на одну корову в год, ц.

Среднее поголовье коров определяется делением общего поголо­вья на число предприятий в группе; среднегодовой надой молока на одну корову — делением валового надоя в группе на общее число ко­ров этой группы; расход кормов на одну голову — делением общего расхода кормов в группе на общее число коров в группе (табл. 4).

Для наглядности, по результатам проведенной аналитической группировки, представленной в таблице 4, строится точечная диа­грамма (рис. 4), характеризующая взаимосвязь факторного и резуль­тативного признака.

Рис. 4, Зависимость продуктивности коров от уровня корлшения по группам

■ В рассматриваемом примере можно сделать следующий вывод: с ростом расхода кормов на одну голову, ц к.ед., увеличивается средне­годовой удой, ц, следовательно, можно предположить наличие пря­мой связи между рассматриваемыми параметрами.

Функциональной называют такую связь, при которой определен­ному значению факторного признака соответствует одно и только од­но значение результативного признака.

Если причинная зависимость проявляется не в каждом отдельном случае, а в среднем при большом числе наблюдений, то такая связь называется стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего зна­чения результативного признака обусловлено изменением факторных признаков.

Связи между явлениями и признаками классифицируются по сте­пени тесноты связи, направлению и аналитическому выражению. По степени тесноты существуют сильные, умеренные и слабые связи. По направлению различают прямую и обратную связи. По аналитиче­скому выражению различают линейные и нелинейные связи.

План изучения темы

1. Методы изучения взаимосвязей социально-экономических яв­
лений [2, с. 184-187; 4, с. 221-224; 6; 7, с. 170-177; 8; 9, с. 323-329].

2. Основы корреляционного и регрессионного анализа. Класси­
фикация корреляционно-регрессионных связей [1, с. 112-116; 2,
с. 187-238; 3, с. 171-183; 4, с. 225-278; 6; 7, с. 177-262; 8; 9, с. 329-353].

3. Оценка существенности связи. Проверка полученной модели
на адекватность [2, с. 244-248; 3, с. 183-186; 6; 7, с. 205-223; 8; 9,
с. 353-361].

4. Построение корреляционно-регрессионных моделей с исполь­
зованием ТП Excel [5, с. 253-342; 10, с. 204-230].

Задание 2. Используя данные статистического наблюдения (табл. 1), проведите корреляционно-регрессионный анализ зависимости между уровнем кормления коров и их молочной продуктивностью, выполнив следующее:

1) постройте точечный график экспериментальных данных, опи­
шите форму и направление связи;

2) оцените тесноту связи с помощью коэффициента корреляции;

3) определите параметры линейного уравнения связи;

4) выполните проверку на адекватность полученного уравнения
корреляционно-регрессионной зависимости по критериям
Фишера, Стьюдента и средней ошибке аппроксимации;

5) на основе построенной регрессионной модели спрогнозируйте
уровень надоя молока на одну корову, если затраты кормов за
год на одну корову составят в среднем 50 центнеров кормовых
единиц;

6) проаншшзируйте влияние изменения расхода кормов на сред­
негодовой удой, рассчитав коэффициент эластичности.

Методика выполнения задания

1. Построение точечного графика экспериментальных данных — это наиболее простой и наглядный способ определения формы и на­правления связи в случае парной корреляции (рис. 5).

Для построения графика надо выделить столбцы Средне­годовой удой и Расход кормов из таблицы 1, выбрать Вставка - Диаграмма - Точечная. Необходимо учесть, что первый столбец Excel автоматически принимает за х, а второй за у, для упрощения процедуры построения столбцы лучше поменять местами.

Рис. 5. Зависимость продуктивности коров от уровня кормления

Анализируя полученный график, легко заметить, что прослежи­вается прямая линейная зависимость между уровнем кормления коров и их молочной продуктивностью, что и было установлено в результа­те проведенной аналитической группировки в задании 1.

2. Оценка тесноты связи между признаками осуществляется с помощью линейного коэффициента корреляции г, который изменяет­ся в пределах от -1 до 1. Чем ближе коэффициент корреляции по мо­дулю к единице, тем сильнее связь между признаками.

Результаты решения выводятся на экран в виде, представленном на рисунке. 7.

Для расчета коэффициента корреляции необходимо ис­пользовать функцию КОРРЕЛ(), в качестве аргумента ко­торой используются ссылки на столбцы Расход кормов и Среднегодовой удой (порядок указания столбцов не имеет значения).

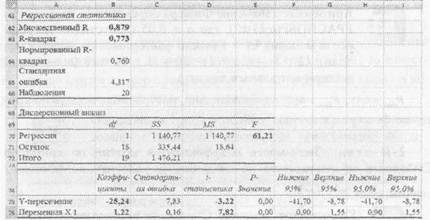
В рассматриваемом примере г = 0,879, что свидетельствует о на­личии сильной связи, положительный знак коэффициента указывает на то, что связь между параметрами прямая.

3. Линейная зависимость может выражаться уравнением прямой линии: у = а_а + а_хх или у = а_хх, где у — продуктивность коров (ре­зультативный признак); х — расход кормов на 1 голову (факторный признак); а₀, а_х — параметры уравнения, которые имеют вполне кон­кретный смысл: а₀ — это величина среднегодового удоя в случае, ес­ли расход кормов х будет равен 0 ц.к.ед., а, — показывает, на сколько центнеров изменится среднегодовой удой от коровы при изменении расхода кормов на 1 ц к.ед.

В каждом конкретном случае необходимо решать, какая из ли­нейных моделей подходит для описания анализируемой предметной области.

Pwc. 6. Диалоговое окно регрессии

Нахождение коэффициентов регрессии осуществляется с помощью пункта меню Сервис - Анализ данных - Рег­рессия (рис. 6).

Рис. 7. Результаты корреляционно-регрессионного анализа

В таблице 5 представлено соответствие показателей, рассчитан­ных с помощью ТП Excel с общепринятой терминологией.

Таблица 5. Соответствие расчетных показателей

Адрес ячейки	Обозначение показателя	Наименование показателя в общепринятой терминологии
В62	г	Коэффициент корреляции
В63	R^2=r^2	Коэффициент детерминации
Е70	Fрасч	Расчетное значение критерия Фишера
В75	а0	Свободный член в регрессионной модели
В76	ах	Коэффициент модели, стоящий перед переменной х
D75	Р^асча0	Расчетное значение критерия Стьюдента для параметра #0
D76	Г"^сча\	Расчетное значение критерия Стьюдента для параметра Ог

Таким образом, в ходе вычислений получили регрессионную мо­дель следующего вида: У = 1, 22х-25,24.

4. Проверка полученной модели на адекватность осуществляется в несколько этапов.

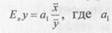
1-й этап. Адекватность модели по критерию Фишера осущест­вляется по следующем}- условию: модель адекватна, если F_rpm <F_pm.

Критическое значение Фишера определяется по формуле FPACnOBP(a;Јl ;к2), где а - 0,05 (допустимая погреш­ность модели), kl = 1 (число факторных признаков в мо­дели), k2 = m-(kl + 1)= 20 - (1 + 1) = 18 (т — число экспериментальных данных).

F_ma =4,41, F_pac4 =61,21, следовательно, построенная модель по кри­терию Фишера адекватна.

значим, если

2-й этап. Значимость коэффициентов модели по критерию Стьюдента осуществляется по следующему условию: коэффициент

Критическое значение Стьюдента определяется по фор­муле СТЬЮДРАСПОБР(<х:&), где а = 0,05 (допустимая погрешность модели), к = т - и = 20 - 2 = 18 (т — число экспериментальных данных, п — число коэффициентов регрессии в модели (а₀ а,)).

Таким образом, расчетные значения критерия Стьюдента ни по одному коэффициенту не превышают критического, можно сделать вывод о значимости коэффициентов «₀, в^.

Если окажется незначим коэффициент а,, то необходимо построить

модель без свободного члена, в случае незначимости коэффициента ^а\ делается вывод о том, что факторный признак выбран не верно.

3-й этап. Оценка качества модели по средней ошибке аппрок­симации, проводится по следующей формуле:

где У, — фактическое значение результативного признака, j, _расч — значение результативного признака, рассчитанного по по­лученной модели, т — число наблюдений.

Средняя ошибка аппроксимации показывает среднее отклонение расчетных значений от экспериментальных. Если А <10%, то качест­во модели считается хорошим, если А > 15%, то делается вывод о не­удовлетворительном качестве полученной модели.

В результате проведенных расчетов

что говорит о хо-

Определение средней ошибки аппроксимации с исполь­зованием табличного процессора представлено на ри­сунке 8.

рошем качестве полученной модели.

можно использовать для

5. Полученную модель

прогнозирования среднегодового удоя на одну корову, ц, при задан­ном расходе кормов на голову, ц к. ед.

Так, если расход кормов на одну голову составит 50 ц к.ед., то среднегодовой удой от коровы составит

6. Коэффициент эластичности определяется по формуле

— коэффициент регрессионного уравнения, х —

среднее значение факторного признака по всей совокупности, у — среднее значение результативного признака по всей совокупности.

¹ В случае незначимости этого коэффициента расчеты следует произвести до кон­ца в учебных целях.

среднее значение расхода среднегодовой надой молока на ко-

равны

В рассматриваемом примере кормов на одну корову, ц к, ед., и рову, ц, рассчитаны в таблице 4 и ент эластичности определяется следующим выражением:

Данное значение свидетельствует о том. что если

расход кормов, ц к. ед., на одну голову увеличить на 1%, это приведет к росту среднегодового надоя на корову, ц, на 1,77%.

Дата добавления: 2014-12-25