Загальнотеоретичні відомості

Вступ

КИЇВ-2012

Методичні вказівки до розрахункової роботи

СИСТЕМИ ТА МЕРЕЖІ ПЕРЕДАЧІ ІНФОРМАЦІЇ

"Методи маршрутизації в телекомунікаційних мережах"

для студентів Фізико-технічного інституту

спеціальності 6.170101 «Безпека інформаційних і комунікаційних систем»

Зміст

Вступ

1. Загальнотеоретичні відомості

2. Завдання до розрахункової роботи

Перелік літератури

Додаткова література

Додатки

Навчальна дисципліна «Системи та мережі передачі інформації» передбачає вивчення основ сучасних телекомунікаційних систем, застосування методів і засобів передачі інформації, формує професійні уявлення про засадничі принципи та особливості функціонування телекомунікаційних систем.

Основний зміст навчальної дисципліни «Системи та мережі передачі інформації» включає наступні розділи:

основи теорії телекомунікації та передачі сигналів;

системи передачі інформації;

сучасні телекомунікаційні мережі;

регулювання діяльності у сфері телекомунікацій;

Метою виконання розрахункової роботи є підготовка студента до самостійної професійної діяльності, систематизація, закріплення та розширення отриманих ним теоретичних знань, набуття практичного досвіду з самостійного вирішення поставлених задач, вивчення та застосування технологій розроблення проектно-звітної та технічної документації, вміння підготувати та оформити результати самостійної роботи.

Одна з головних проблем експлуатації телекомунікаційних мереж (ТКМ) – проблема керування потоками інформації, зокрема, проблема маршрутизації. Маршрут – це низка (послідовність) суміжних вузлів ТКМ, якою забезпечується передача інформації від вузла джерела (ВД) (вузла-відправника (ВВ)) інформації до вузла отримувача (ВО) [1]. У відповідності до цього визначення типовою формою представлення (опису) маршруту доставлення інформації від ВД до ВО є кортеж: , де у вуглових лапках <...> на першій позиції вказується номер ВД, далі розташовано низку номерів транзитних вузлів , якими передається інформація, останню позицію кортежу займає номер ВО.

Мета маршрутизації – вибір в ТКМ найкоротшого шляху доставлення інформації від ВД до ВО. Під найкоротшим розуміється шлях, що забезпечує мінімальний інтервал часу між відправленням та отриманням інформації.

На жаль, щільність інформаційних потоків та умови транспортування інформації в ТКМ можуть суттєво змінюватися впродовж часу доби, тижня, сезону, року й т.п., що залежить від цілого ряду причин. Це впливає на поточну швидкість передачі інформації в різних фрагментах ТКМ, істотно ускладнюючи маршрутизацію із застосуванням часового показника довжини маршруту. Тому вибір найкоротшого маршруту значно спрощується, якщо його здійснювати за фізичною довжиною маршруту або за довжиною, виміряною у транзитах: один транзит – ділянка між двома сусідніми вузлами ТКМ [2]. В цьому випадку вибір маршруту реалізується за критерієм мінімальної кількості транзитів:

, , (1)

де – довжина маршруту , виміряна в транзитах.

Для розв’язання задачі маршрутизації у кожному вузлі ТКМ треба сформувати таблицю маршрутизації, яка представляє собою матрицю вимірності , де s – кількість вузлів ТКМ, 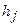– кількість вихідних ліній зв’язку (ЛЗ) з j –ого вузла:

, , . (2)

Наприклад, для для другого вузла ТКМ, зображеної на Рис.1.1, маємо (j =2, s =4, h₂ =3):

, (3)

де – вектор-рядок, перший елемент якого містить відомості про пріоритети вибору вихідних ЛЗ при передачі інформації від вузла 2 (ВД) до вузла 1 (ВО). Найвищий пріоритет має вихідна ЛЗ, яка безпосередньо транспортує інформацію з вузла 2 до вузла 1 (так звана вихідна першого вибору, представляє найкоротший шлях від вузла 2 до вузла 1), нижчий пріоритет у вихідної ЛЗ, яка транспортує інформацію від вузла 2 до вузла 1 через вузол 4 (вихідна другого вибору), найнижчий пріоритет – у вихідної ЛЗ, що

Рис.1.1

передає інформацію від вузла 2 до вузла 1 найдовшим шляхом через вузли 3, 4 (вихідна третього вибору). Три наведені вище вихідні ЛЗ визначають вимірність вектора та зміст його елементів (координат, позицій). На першій позиції вектора стоїть 1 – номер вузла, до якого спрямовано вихідну ЛЗ першого вибору, другу позицію займає 4 – номер вузла, до якого спрямовано вихідну ЛЗ другого вибору, відповідно третю позицію займає 3 – номер вузла у напрямі вихідної ЛЗ третього вибору. Вектор-рядок – визначає пріоритети вибору вихідних ЛЗ при передачі інформації від вузла 2 (ВД) до вузла 3 (ВО), а вектор-рядок 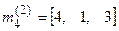– від вузла 2 до вузла 4.

Аналогічним чином можна сформувати ще три матриці, що визначають пріоритети вихідних ЛЗ інших ВД для ТКМ, зображеної на Рис.1:

, , . (4)

Сукупність таблиць маршрутизації для всіх вузлів ТКМ зветься планом розподілу інформації (ПРІ) на мережі зв’язку. ПРІ дозволяє визначити маршрути між будь-якою парою вузлів ТКМ. Для цього потрібно звернутися до таблиць маршрутизації вузлів мережі, починаючи з таблиці маршрутизації для ВД (тобто j – це номер ВД), де вибрати вектор-рядок 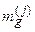, нижній індекс якого співпадає з номером ВО. Перший елемент цього вектору є номером першого вузла маршруту і одночасно вказує індекс наступної таблиці маршрутизації, яка містить відомості про другий вузол маршруту, номер якого в свою чергу визначить індекс чергової таблиці маршрутизації і т.д. Якщо до маршруту увійдуть тільки номери вузлів, які відповідають першому елементу вектор-рядків таблиць маршрутизації, це означає, що до маршруту залучено тільки вузли, до яких прямують вихідні ЛЗ першого вибору, тому отриманий маршрут буде найкоротшим.

Якщо з певних причин деякі з цих вузлів виявляться недоступними, у маршрут замість заблокованого вузла слід ввести вузол, до якого спрямовано вихідну ЛЗ другого вибору (друга позиція вектору 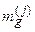), а в разі недоступності і цього напряму використати вихідну третього вибору (третя позиція вектору 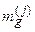) і т.д. Очевидно, що отриманий в цьому випадку маршрут буде мати більшу довжину.

Для досить розгалужених, складних ТКМ проблема визначення вихідних ЛЗ різного вибору та формування таблиць маршрутизації є досить важкою і потребує чіткої алгоритмізації свого вирішення. В ТКМ порівняно невеликих масштабів ця задача вирішується методом рельєфів [1], який базується на алгоритмі Белмана-Форда [3].

Розглянемо суть методу рельєфів на прикладі побудови таблиці маршрутизації для довільного j-ого вузла мережі. Передамо всіма вихідними ЛЗ цього вузла число 1. Далі із всіх вузлів, що отримали 1, передамо по їх вільним вихідним ЛЗ (усі вихідні ЛЗ, окрім тих, якими поступила 1) число 2. З вузлів, які отримали 2, передамо відповідними вільними вихідними ЛЗ число 3 і т. д., доки на передачу числової інформації не будуть задіяні всі ЛЗ, тобто у відповідність кожній ЛЗ буде поставлене певне чисельне значення (те число, яке передаватиметься цією ЛЗ), яке назвемо висотою ЛЗ. Повну сукупність пронумерованих у такий спосіб ЛЗ мережі назвемо j -рельєфом мережі. Маючи j -рельєф, можемо для кожного вузла мережі визначити впорядковану множину вихідних ЛЗ: вихідною ЛЗ першого вибору буде ЛЗ мінімальної висоти, більш високі ЛЗ стануть відповідно вихідними другого, третього і більш високого вибору.

Проілюструємо застосування методу рельєфів на прикладі побудови А-рельєфу для ТКМ, зображеної на Рис.1.2.

Рис.1.2

Від вузла А вихідними АВ, AC, AD передамо число 1, яке визначатиме висоту кожної з цих вихідних. Із суміжних з А вузлів В, С, D, що отримали 1, передамо до вузлів G, I, K число 2, яке визначить висоти відповідних ЛЗ (див. Рис.1.2). В свою чергу вузли G, I, K передадуть число 3 наступній групі вузлів L, M, H, O. Останнє число 4 завершить процес нумерації ЛЗ та побудови А-рельєфу, кінцеві результати якого представлено на Рис.2.

Щоб знайти найкоротший маршрут від довільного ВО до вузла А (який для даного А-рельєфу є фіксованим ВД), достатньо, починаючи з обраного ВО і йдучи від нього в зворотному напрямі до вузла А, вибирати ЛЗ найменшої висоти. Так, якщо у якості ВО виступає вузол N, маємо три найкоротших маршрути: < A, D, K, O, N >, 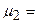< A, C, I, M, N >, < A, C, K, O, N >.

Особливістю викладеного вище підходу до розв’язання задач маршрутизації є можливість пристосування маршруту до поточних змін стану мережі, обумовлених змінною довжиною черг в вузлах мережі протягом певного часового інтервалу, змінами топології мережі внаслідок перевантаження та тимчасового блокування окремих вузлів та ЛЗ, впливом зовнішніх факторів на функціонування технічних засобів та устаткування ТКМ. Такий спосіб формування маршрутів, в якому реалізується динамічне корегування таблиць маршрутизації та безпосередньо маршрутів відповідно до змін стану мережі, називається адаптивною маршрутизацією. На жаль, оперативний контроль стану мережі вимагає дуже високих накладних витрат, які ще називають системними витратами [4]. Це обумовлює актуальність розробки та застосування способів маршрутизації, які б у своїй реалізації спиралися на певну статистичну ретроспективу про характеристики ТКМ.

Зокрема, можливе спрощення задачі адаптивної маршрутизації полягає в контролі стану лише незначної кількості окремих транзитних вузлів мережі, котрі за досвідом попередньої експлуатації і відповідною статистикою сприяють утворенню так званих вузьких місць, в яких ймовірне виникнення тимчасового блокування локального мережного трафіку. Врахування статистичної інформації про стан таких вузлів ТКМ полягає у визначенні оцінок ймовірності блокування передачі інформації через ці вузли, й введення отриманих оцінок до таблиці маршрутизації разом з номерами відповідних вузлів. В разі включення подібних вузлів у склад маршруту відомості про можливе блокування проходження інформації цими вузлами мають бути використані для обчислення ймовірності успішного використання відповідного і -ого маршруту. За своєю структурою ймовірність являтиме добуток двох ймовірностей: - ймовірності застосування і -ого маршруту та - ймовірності відсутності блокування інформації при її передачі маршрутом. При формуванні маршрутів у звичайний спосіб з використанням інформації про вихідні ЛЗ першого, другого вибору (та більш високого вибору) отримаємо групу найкоротших маршрутів, що на жаль ніяк не виключає можливість потрапляння до складу цих маршруту вузлів з можливим блокуванням трафіку. В останньому випадку ймовірність успішного використання цієї групи маршрутів буде нижче за одиницю. Успішну передачу інформації за певним маршрутом можна гарантувати лише за умов відсутності у складі маршруту вузлів з ненульовою ймовірністю блокування. Однак довжина такого маршруту звичайно буває доволі значною. Оптимізація рішення задачі маршрутизації в цих умовах полягає у формуванні так званої повної групи впорядкованих за довжиною маршрутів: від найкоротшого (маршруту першого вибору), отриманого з використанням відомостей щодо вихідних ЛЗ першого вибору, до більш довгих (маршрутів старшого вибору) та, кінець-кінцем, до найдовшого в групі (маршруту останнього вибору), який є найкоротшим з маршрутів, що не містять вузлів з ймовірним блокуванням передачі інформації. Більш довгі маршрути формуються на основі раніше отриманих коротших шляхом обходу (не використання) вузлів, в яких існує можливість блокування передачі інформації. Ця процедура реалізується або у звичайний спосіб (із застосуванням для реалізації обходу вихідних ЛЗ старшого вибору), або шляхом виключення із схеми ТКМ непрохідних (заблокованих) вузлів і визначення на оновленій таким чином схемі найкоротшого маршруту. В останньому випадку процедура побудови маршруту є більш прозорою, але й більш трудомісткою, бо процес побудови кожного разу відтворюється фактично заново для структурно спрощеної (через виключення непрохідних вузлів) мережі.

Залежно від поточного стану мережі, передача інформації здійснюється найкоротшим з незаблокованих на поточний момент маршрутів. Якщо стан мережі наблизився до критичного, передача інформації гарантовано реалізується маршрутом останнього вибору.

Виділення повної групи маршрутів різної довжини, які в сукупності гарантують передачу інформації між заданими ВД і ВО, дозволяє за умов можливості отримання оцінок ймовірності використання кожного із маршрутів, підрахувати, яка в середньому буде довжина маршруту, за яким передаватиметься інформація впродовж достатньо довгої експлуатації ТКМ. Наприклад, якщо знайдено повну групу маршрутів між вузлами ВД і ВО: 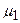, , , довжини яких відповідно дорівнюють , , , 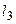причому 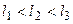, а ймовірності успішного використання маршрутів становлять , , , то розрахункова середньоймовірна довжина маршруту між цими вузлами визначиться за формулою:

. (5)

Розглянемо розв’язок цієї задачі більш детально. Нехай структура ТКМ буде задана наведеною нижче схемою (Рис.1.3), вузли ВД і ВО співпадатимуть з вузлами 10 і 37, блокування передачі інформації можливе у вузлах 11, 18, 19 з ймовірностями відповідно 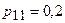; ; 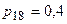. Потрібно визначити сукупність маршрутів, яка б гарантувала отримання інформації вузлом ВО за умов мінімізації середньоймовірної довжини маршруту.

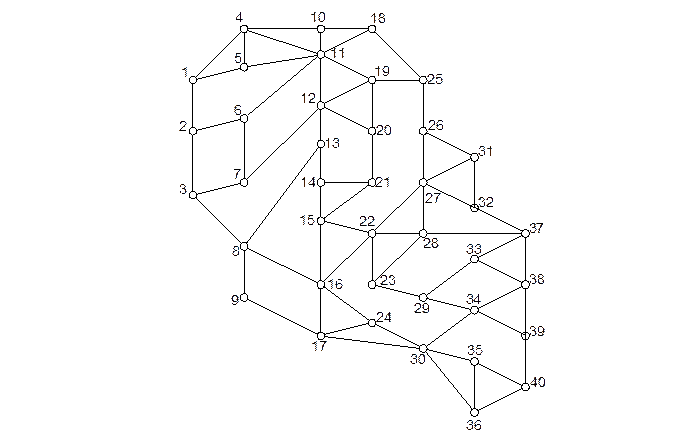Рис.1.3

Зауважимо, що отримати розв’язок подібної задачі можна кількома способами. Розглянемо два з них.

Дата добавления: 2014-12-25