Спосіб 1

Зміст цього способу полягає у аналізі можливих маршрутів передачі інформації від ВД до ВО, починаючи з найкоротшого маршруту. Якщо він містить вузли, в яких присутнє блокування передачі інформації, до розгляду додаються більш довгі маршрути, аж доки не отримаємо маршрут, для якого ймовірність блокування дорівнюватиме 0.

У нашому випадку маємо два найкоротших маршрути (маршрути першого вибору), представлених кортежами, що містять номери послідовних вузлів, з яких утворюється відповідний маршрут:

, , .

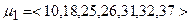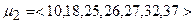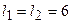З точки зору можливостей їх застосування ці маршрути тотожні, бо мають однакову довжину в шість транзитів й обидва містять транзитний вузол 18, який з ймовірністю 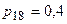припускає блокування передачі інформації. Зважаючи, що це найкоротші маршрути, ймовірність їх застосування дорівнює 1, ймовірність відсутності блокування у вузлі 18 дорівнює 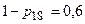, то ж маємо ймовірності успішного використання [5-7]:

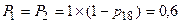. (6)

Наступними за довжиною будуть маршрути та 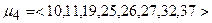, , 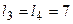котрі як і два попередні тотожні між собою за своїми експлуатаційними характеристиками. У цих двох маршрутах інформацію може бути заблоковано у вузлах 11, 19, тобто ймовірність відсутності блокування даних маршрутів дорівнюватиме 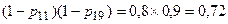. Ймовірності застосування цих маршрутів дорівнюють = = 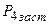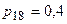(застосування маршрутів відбудеться у випадку блокування маршрутів 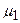, ), звідки 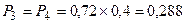. Далі аналізуватиметься група маршрутів довжиною у 8 транзитів:

,

,

.

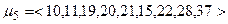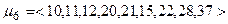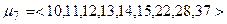Маршрут 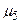за умовами успішного використання тотожній маршрутам 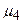, , 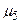однак довший за них, через що в його аналізі немає сенсу. Маршрути 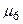, 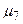застосовуються за умов блокування інформації у вузлах 18, 19, тобто

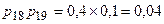= = , (7)

ймовірність відсутності їх блокування однакова і дорівнює 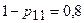, то ж ймовірність їх успішного використання визначається як

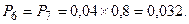(8)

Наступна група маршрутів серед інших містить маршрут, у складі якого відсутні вузли з можливим блокуванням інформації (тобто маршрут останнього вибору): 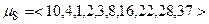.Очевидно, що можливість блокування інформації для нього дорівнює 0, тобто 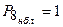, умовою застосування є блокування попередніх маршрутів, а саме, блокування транзитних вузлів 11, 18. Тому ймовірність застосування цього маршруту співпадає із ймовірністю його успішного використання:

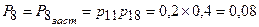. (9)

Доведення процедури пошуку маршрутів до виявлення маршруту, що не містить вузлів з можливим блокуванням, є ознакою припинення подальшого аналізу ТКМ. Перевірити це можна, підрахувавши суму обчислених ймовірностей успішного використання маршрутів, яка повинна дорівнювати одиниці. Відповідно з отриманими вище результатами, беручи з кожної групи однакових за довжиною маршрутів перший, маємо: 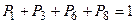, тобто зроблений аналіз не містить помилок.

Підрахуємо середньоймовірну довжину маршруту:

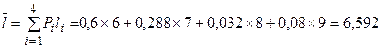(10)

Як бачимо, через можливе блокування передачі інформації в ТКМ, середньоймовірна довжина маршруту на 0,592 транзити довше найкоротших маршрутів , .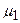

Дата добавления: 2014-12-25