Спосіб 2

Цей спосіб розв’язання задачі має дещо більш формальний характер порівняно із першим способом.

Для заданих ВД і ВО спочатку визначимо сукупність можливих маршрутів, починаючи з найкоротшого і поступово збільшуючи довжину маршруту доти, доки не буде знайдений самий короткий маршрут, в якому відсутні транзитні вузли з можливим блокуванням передачі інформації. В цій сукупності виділимо групи маршрутів, що містять однакові набори (сполучення) вузлів, у яких існує можливість блокування передачі інформації, і залишимо для наступного аналізу по одному найкоротшому представнику кожної групи. Наприклад, подібну групу утворюють маршрути , , 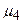, 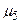до складу кожного з яких входить сполучення вузлів 11, 19. Очевидно, що для подальшого аналізу слід виключити з розгляду найдовший в цій трійці маршрут 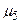й залишити лише один з коротких маршрутів ( або 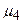), абсолютно тотожних за своїми експлуатаційними характеристиками (однакова довжина маршруту та ймовірність блокування).

Припустимо, що для нашої задачі після виконання викладеного вище попереднього аналізу отримано таку сукупність маршрутів:

, ,

, ,

, ,

, .

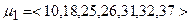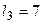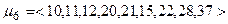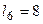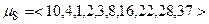Далі проведемо аналіз можливих станів групи транзитних вузлів 11, 18, 19, кожен з яких може бути або заблокованим, або ні. Загалом комплекс з трьох означених вузлів може перебувати в одному з 2³=8 станів, кожен з яких характеризується своєю ймовірністю 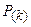. Нижче наведено структуру ймовірнісних характеристик цих станів, (ймовірність відсутності блокування інформації у відповідному j -ому вузлі позначається як ), у круглих лапках вказано номер стану комплексу:

(1) ,

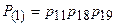(2) ,

(3) ,

(4) ,

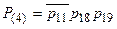(5) ,

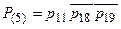(6) ,

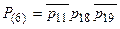(7) ,

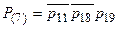(8) .

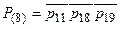Якщо розглядати кожний з наведений вище станів як певну подію, отримаємо повну групу попарно несумісних подій [6,7], для якої .

Визначимо, які з восьми наведених вище подій реалізуються в маршрутах 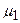, , , , 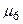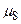гарантуючи відсутність блокування відповідного маршруту. Почнемо з найкоротшого маршруту 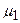. Очевидно, що використання цього маршруту можливе у разі реалізації подій (3), (5), (7), (8), для яких характерна відсутність блокування інформації у вузлі 18, тобто

,

так як сума ймовірностей у круглих дужках дорівнює 1 (це повна група подій для сукупності можливих станів пари вузлів 11 та 19).

Для маршруту довжиною 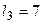відсутність блокування інформації гарантується реалізацією стану (6), тобто

.

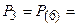
Аналогічним чином для маршрутів 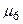, 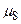маємо:

,

.

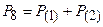
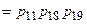
Як бачимо, всі вісім можливих станів комплексу транзитних вузлів 11, 18, 19 ввійшли до складу виділеної сукупності маршрутів , то ж обрана сукупність маршрутів гарантує доставлення інформації від ВД до ВО за будь-якого стану комплексу і не потребує введення додаткових маршрутів.

Отримані результати розрахунків ймовірностей Р ₁, Р ₃, Р ₆, Р ₈ повністю співпадають із результатами, обчисленими при розв’язку задачі маршрутизації у першій спосіб, тобто використання другого способу розв’язання задачі фактично є взаємоперевіркою обох рішень, позитивний наслідок якої підтверджує їх обоюдну вірність.

Дата добавления: 2014-12-25