Встречно-параллельное соединение звеньев

Встречно-параллельным соединением двух звеньев называется такое соединение, при котором выходной сигнал первого звена подаётся на вход второго, а выходной сигнал второго звена с соответствующим знаком суммируется с общим входным сигналом и подаётся на вход первого звена. Общим выходным сигналом является выход первого звена (рисунок – 3.4).

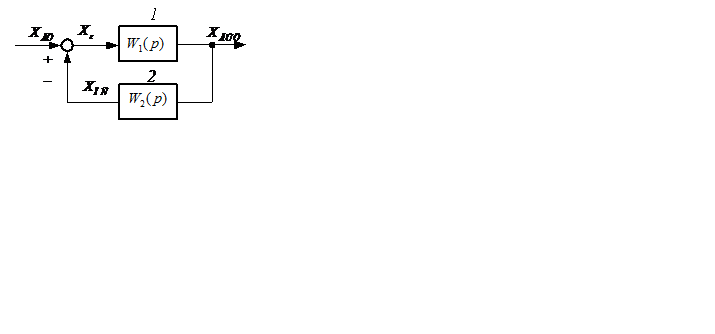Звено, в котором направление передачи сигнала совпадает с направлением передачи общего сигнала (первое звено), называется звеном прямой связи, а звено, в котором направление передачи сигнала противоположно направлению передачи общего сигнала (второе звено), называется звеном обратной связи.

Если знак сигнала обратной связи положителен, т.е. если он суммируется с общим сигналом, то обратная связь называется положительной. Если знак сигнала отри

цателен, т.е. он вычитается из общего сигнала, то обратная связь называется отрицательной.

Рассмотрим встречно-параллельное соединение на примере двух звеньев. Опишем эту систему

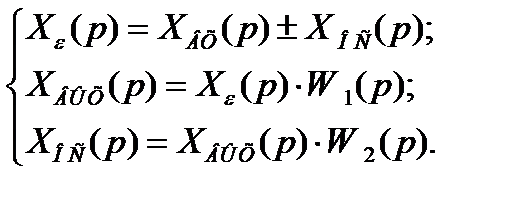(3.24)

В системе уравнений (3.24) знак «+» соответствует положительной, а знак «-» - отрицательной обратной связи.

В результате решения, получаем

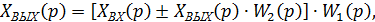
откуда

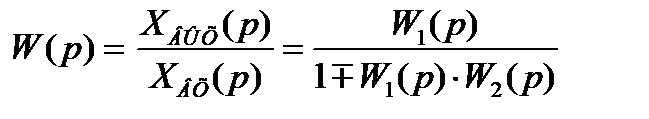, (3.25)

Знак «-» в (3.25) соответствует положительной, а знак «+» - отрицательной обратной связи.

Для получения АФЧХ заменим в передаточной функции p на jω:

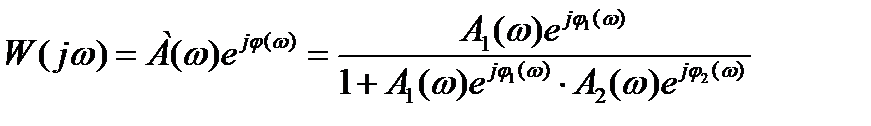, (3.26)

Рассмотрим два случая.

1 случай:

Допустим, что в некотором диапазоне частот

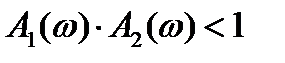, т.е.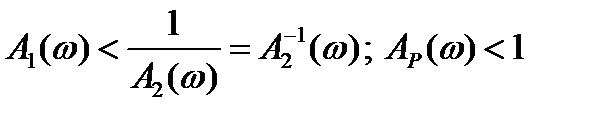

В этом случае выражение (3.26) удобно записать в виде:

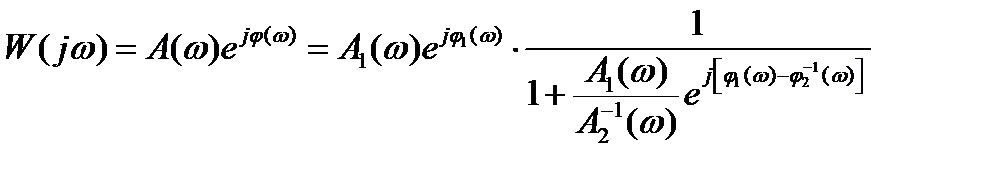, (3.27)

где 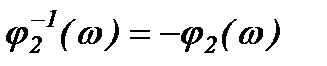- обратная ФЧХ второго звена (звена обратной связи).

Обозначим ,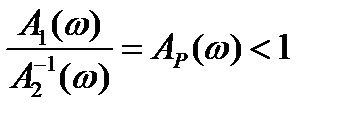

,

.

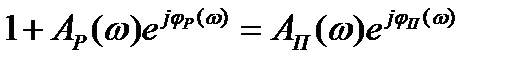Тогда выражение (3.27) примет вид

.

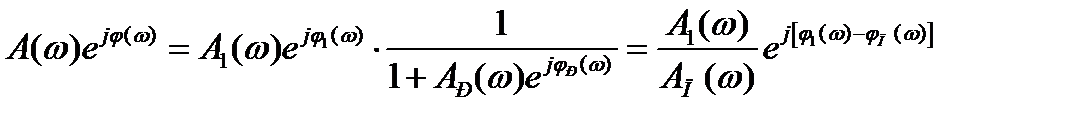откуда искомые

АЧХ ,

ФЧХ 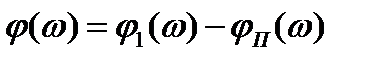. (3.28)

Переходя к логарифмическому масштабу

, (3.29)

,

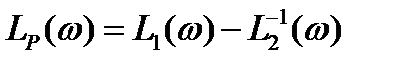где 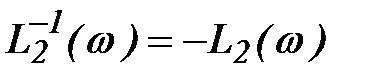- обратная ЛАЧХ второго звена.

Из выражений (3.28), (3.29) следует, что искомые ЛАЧХ и ФЧХ находятся путем вычитания поправочных ординат из характеристик первого звена, т.е. характеристики звена ЛАЧХ, которое проходит ниже.

2 случай:

, т.е. .

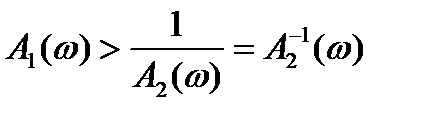В этом случае выражение (3.26) удобно представить в виде:

.

Обозначив ,

,

,

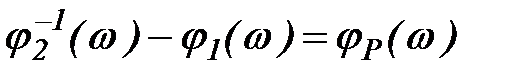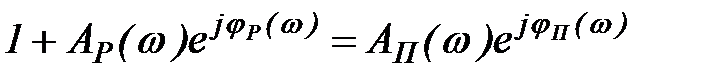получим

.

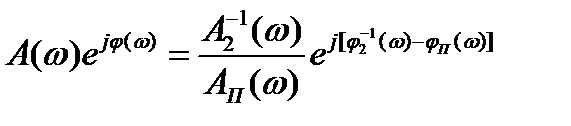Переходя к логарифмическому масштабу

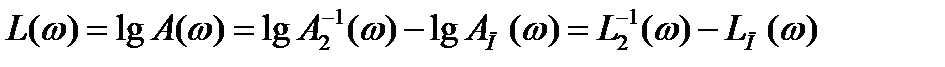, (3.30)

. (3.31)

Из выражений (3.30), (3.31) следует, что искомые ЛАЧХ и ФЧХ находятся путем вычитания поправочных ординат из обратных ЛАЧХ и ФЧХ второго звена, т.е. опять-таки из характеристики звена ЛАЧХ, которого проходит ниже.

Если поправочные ординаты малы, то результирующая ЛАЧХ совпадает с нижележащими участками характеристик. Результирующая ФЧХ совпадает с характеристиками ЛАЧХ, которая проходит ниже.

1. Таким образом, для построения характеристик встречно-параллельного соединения звеньев вычерчивается ЛЧХ звена прямого канала и обратная ЛЧХ звена, находящегося в цепи обратной связи 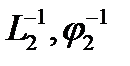. Результирующая ЛАЧХ проходит по низам с учетом поправок.

2. Поправки можно найти следующим образом:

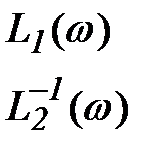
Для более оперативного отыскания поправок, исходя из векторной диаграммы для поправочного вектора может быть построена номограмма.

Следовательно, суммарная ЛАЧХ проходит по ЛАЧХ того звена, ЛАЧХ которого лежит ниже; суммарная ЛФЧХ проходит по ЛФЧХ того звена, ЛАЧХ которого лежит ниже с учётом поправок.

Дата добавления: 2014-12-25