Линеаризация статических характеристик

Применяют линеаризацию статическую и динамическую.

- Статическая линеаризация.

Рисунок 4.2 – Статическая (а) и динамическая (б) линеаризации

Кривая заменяется прямой (рисунок 4.2,а) в соответствии с каким-либо законом. Например, методом наименьших квадратов.

- Динамическая линеаризация.

В точке А кривой находится и заменяется при этом кривая линейным законом (рисунок 4.2, б).

а) Функция одной переменной.

Пусть дана статическая характеристика – непрерывная дифференци­руемая функция y =f(x), причем точкой основного режима рабо­ты является точка А.

Рисунок 4.3 – Динамическая линеаризация

Разложим функцию в степенной ряд Тейлора в рабочей точке А

(4.3)

.

При рассмотрении изменения x в окрестностях точки А в неболь­шом диапазоне возможно ограничиться рассмотрением 2-х первых членов ряда Тейлора

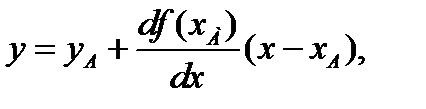
(4.4)

где x – x_A = Δx – отклонение x от исходного значения;

y – y_A = Δy – отклонение y от исходного значения.

Тогда ,

где – коэффициент связи между y и x в окрестностях точки А или коэффициент усиления элемента в окрестности исходной точки.

На структурной схеме последнее уравнение изобразится рисунок 4.4.

Рисунок 4.4

Пример 4.1. Дано уравнение y=x²+x+1 линеаризовать его в точке х_А=1..

Находим производную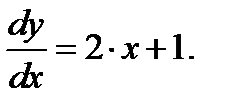

Тогда k(А)=3.

б) Функция двух переменных.

Пусть дана статическая характеристика в виде непрерывной дифференцируемой функции двух переменных (рисунок 4.5)

z = f(x,y). (4.5)

Точкой основного режима работы является точка А.

Рисунок 4.5 – Функция двух переменных

\

Разложим функция в степенной ряд Тейлора в точке А:

.

(4.6)

При небольшом отклонении x, y от рабочей точки А также допустимо ограничение двумя членами ряда Тейлора

. (4.7)

Обозначим

,

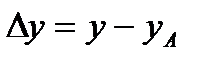тогда уравнение (4.7) запишется в виде

. (4.8)

Обозначим .

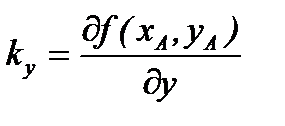На структурной схеме это уравнение отобразится (рисунок 4.6)

Рисунок 4.6

Пример 4.2. Дана функция z=2x²+y+3, линеаризовать её в точке х_А=1; у_А=2.

Найдём частные производные

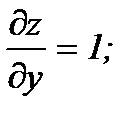тогда k_x=4; k_y=2.

4.3 Передаточная функция в установившемся режиме

Структурная схема для установившегося режима составляется на основе уравнений элементов САУ в статике или на основе линеаризованной структурной схемы САУ формальным путём приравнивания опе­ратора p к нулю.

Пример 4.3. Дана структурная схема САУ. Вычислить общий коэффициент усиления (передаточную функцию в установившемся режиме).

Поведение системы в переходном процессе (в динамике) происходит в соответствии передаточной функцией

Общий коэффициент усиления (установившийся режим) получим, заменяя р на нуль.

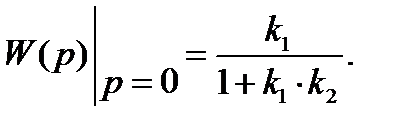
Дата добавления: 2014-12-25