Переход через нулевой уровень

Пересекающие нулевой уровень события (и соответствующие блоки палитры Treshold) введены, чтобы преодолеть трудность в моделировании непрерывных систем, когда есть некоторые «прерывания», т.е. резкие изменения (скачки) сигналов. Эти явления могут вызвать ошибки при использовании используемых методов интеграции. Численный решатель Scicos, благодаря механизму обнаружения моментов перехода через ноль, может обнаружить такие события. Для обычных случаев в Scicos используется блок пересечения нуля. Цель этого блока состоит в том, чтобы при обнаружении «разрывов» (скачков) сигналов производить переключения уравнений системы.

Применение блоков пересечения нуля чаще всего необходимо в гибридных моделях для непредсказуемых событий. Например, при моделировании системы контроля уровня жидкости в резервуаре в случае прекращения притока, как только уровень превысит определенную величину.

В некоторых приложениях, в дополнение к установлению факта пересечения, мы должны знать направление пересечения.

В этих целях в Scicos имеются два других блока: блок «+ to –» и блок «– to +», которые фиксируют не только факт пересечения, но и учитывают направление этого пересечения.

Покажем простой сеанс Scicos, чтобы проиллюстрировать использование блоков нулевого пересечения.

Мы уже столкнулись с часами активации Event Clock, которые генерировали последовательность равномерно расположенных во времени событий. Они были использованы, чтобы активизировать Scope. Откроем пустое окно Scicos. Создадим следующую модель, копируя блоки из палитр.

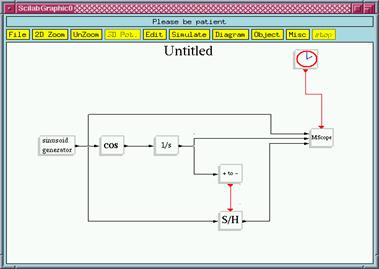
Блок «+to-» находим в палитре Treshold, S/H-блок (sample and hold, образец и сохранение) – в палитре линейных блоков и cos-блок – в нелинейной палитре. Отметим, что блок MScope имеет 3 входа. Количество входов MScope является параметром блока; его нужно установить прежде, чем входы будут подсоединены.

Блок «+to-» генерирует событие каждый раз, когда входной сигнал пересекает нулевой уровень, изменяясь от плюса к минусу. Входной сигнал должен быть непрерывной функцией времени. Эти события активизируют блок S/H, который копирует входной сигнал (образец) на свой выход. Сигнал на выходе не изменяется до следующей активации блока.

Результат счета показан на рисунке.

Параметр амплитуды блока генератора sinusoid установлен 8.7. События, с выхода блока пересечения нулевого уровня, были использованы для генерации дискретных сигналов. Эти дискретные сигналы могут быть использованы в свою очередь для управления непрерывными компонентами. Это часто делается в управляющей системе, где дискретные контроллеры управляют непрерывными системами. Простой пример:

Дискретный сигнал возвращается в непрерывную часть схемы. Отметим, что у генератора прямоугольных волн выходной порт слева (в линейной палитре, выход у этого блока справа). Это сделано посредством использования команды Flip в меню Editor. Этот блок выдает на выход 0 или 1, переключение производится сигналом активации. Результат моделирования показан ниже.

Дата добавления: 2014-12-25