Ш. Класифікація за характером зміни задаючої величини (за призначенням системи, або за алгоритмом керування)

У різних підручниках використовується різна назва:

- системи стабілізації;

- слідкуючі системи;

- системи програмного керування.

- системи екстремального керування.

Системи стабілізації - це такі системи, в яких задаюча величина є постійною, а завданням системи керування є забезпечення постійного значення вихідної величини Алгоритм функціонування в таких САК може бути записаний у вигляді: y(t)=const. Прикладом таких систем може бути холодильник, АРУ радіоприймача, генератор електричного струму, регулятор швидкості двигуна і т.п.

Слідкуючі системи - це такі системи, в яких вхідна величина змінюється випадковим чином а завданням системи є забезпечення відповідної зміни вихідної величини.

У таких системах алгоритм функціонування завчасно невідомий; його можна записати у вигляді: y_б(t)=F[x(t)], де функція F задана, а закон зміни задавальної дії x(t) невідомий. Власне слідкуюча система має алгоритм функціонування y_б(t)=x(t), тобто вихідна координата повинна із заданою точністю відтворювати сам задавальний вплив. У більш загальному випадку слідкуючі системи не тільки слідкують за задавальним впливом, але й перетворюють його за певним законом

Оскільки в слідкуючих системах вхідний вплив являє собою випадкову величину, то для забезпечення високої якості регулювання система повинна мати регулятор (КП) з високою швидкодією і високою точністю.

Прикладом таких систем є системи керування зенітним вогнем, ракета типу земля-повітря, торпеди, копіри для розкрою металу, тканини і т.п.

Системи програмного керування - це системи у яких задаюча величина змінюється за відомим наперед законом і завданням системи є забезпечення відповідної зміни вихідної величини.

Алгоритм функціонування таких систем може бути записаний у вигляді y_б=F[x(t)], де функція F і дія x(t) наперед визначені.

У реальних системах використовуються два види керування: з часовою програмою і з просторовою програмою. У першому випадку ЗП виробляє безпосередньо функцію x(t). У системах з просторовою програмою рух виконавчого органу (інструменту верстатів, захвату роботів, тощо) здійснюється за заданою в просторі траєкторією.

Прикладом таких систем є верстати з програмним керування, теплові печі для теплової обробки металів і т. п. У принципі їх робота аналогічна слідкуючим системам, але оскільки закон зміни вхідної величині відомий, то такі САК можуть бути дещо простішими за своєю будовою.

Системи екстремального керування здійснюють пошук екстремуму деякої функції і забезпечують роботу в режимі, близькому до екстремуму. Наприклад, система, що забезпечує настроювання радіоприймача на частоту передавальної станції за найбільшою гучністю прийому або за найбільшою яскравістю свічення індикаторної лампи. Необхідним елементом у такій системі є чутливий елемент, що знаходить екстремум.

Оскільки в системах екстремального керування вимірюється значення керованої координати, вони належать до класу систем керування за замкнутим контуром.

ІV. Класифікація за кількістю вихідних координат системи:

- одномірні;

- багатовимірні.

Одномірні системи - це системи, які керують тільки за однією вихідною величиною, наприклад, холодильник, двигун з регулятором швидкості, є одномірними системами.

Багатовимірні системи - це системи, які здійснюють керування за декількома вихідними величинами. Наприклад, САК зенітної ракети здійснює керування як за напрямком руху (азимутом), так і за нахилом до горизонту. САК генератора електростанції виконує керування за частотою та напругою.

Серед багатовимірних САК розрізняють системи зі зв’язаним і з незв’язаним керуванням. САК зенітної ракети має незв’язане керування, оскільки керувати рухом за азимутом може одна системи, а рухом за кутом нахилу до горизонту інша незалежна система. У випадку електричного генератора ситуація дещо складніша, оскільки зміна частоти обертання генератора приводить і до зміни напруги, тому система керування повинна бути дещо складніша, щоб забезпечити потрібну частоту струму при заданій величині напруги. Така система керування є зв’язаною.

V. За характером рівнянь, які описують систему:

- лінійні;

- нелінійні.

Лінійні системи - це системи, які описуються лінійними диференційними рівняннями. Для лінійних систем справедливий принцип суперпозиції. Принцип суперпозиції (накладання) полягає в тому, що реакція системи на суму дій пропорційна сумі реакцій на кожну дію зокрема. Наприклад на рис. 2.7 показано стрілу прогину дошки. Якщо виправдовується правило суперпозиції, то загальна стріла прогину при двох вантажах дорівнює сумі стріл прогину кожного вантажу окремо, і система є лінійною. Принцип суперпозиції може виконуватись в якихось певних межах навантажень. Діапазон, в якому справедливий принцип суперпозиції називають діапазоном лінійності.

Нелінійні системи – це системи, в яких хоча б для однієї ланки не виконується принцип суперпозиції. Такі системи описуються нелінійними диференційними рівняннями. Аналіз їх складніший, ніж лінійних систем. Досить часто вдається звести аналіз нелінійних до аналізу лінійних систем. Методи такого приведення називаються лінеаризацією і будуть розглянуті далі.

Рис. 2.7 – Демонстрація принципу суперпозиції реакції лілійних систем

VІ. За характером дії в часі:

- безперервної дії;

- дискретної дії.

Системи безперервної дії складаються тільки з ланок, в яких вихідна величина плавно змінюється протягом часу. У безперервній системі сигнали на виході її елементів є безперервними функціями. Між елементами системи існує безперервний функціональний зв’язок. Безперервні системи описуються диференціальними рівняннями. Безперервною CAP є система, її якій структура всіх зв'язків у процесі роботи не змінюється і величина па виході кожного елемента є неперервною функцією збурення і часу.

САК називається дискретною, якщо вихідна величина будь-якого з її елементів має дискретний характер. Перетворення безперервних сигналів на дискретні пов’язано з наявністю в системі дискретного елемента. Дискретні системи описуються диференціально-різницевими рівняннями.

Розрізняють такі дискретні системи:

· релейні;

· імпульсні,

· цифрові.

У системах релейної дії вихідна величина змінюється при деяких граничних значеннях вхідної величини, в системах імпульсної дії – через певні проміжки часу, а в цифрових системах і те, й інше.

Переваги перервних (імпульсних) систем полягають у періодичному характері їх дії, що дає змогу зменшити знос елементів системи і збільшити її надійність, підвищити техніко-економічні показники системи керування, виготувати вимірювальні елементи більшої чутливості, збільшити точність системи.

Системи перервної дії в основному використовуються при малій швидкодії, де їх переваги виявляються найбільшою мірою.

VII. За зміною параметрів системи в часі САК поділяють на:

- стаціонарні;

- нестаціонарні.

Стаціонарна система - це така система, параметри якої незмінні протягом часу.

Нестаціонарна система має параметри, які змінюються з часом. При математичному описі таких систем деякі коефіцієнти диференційного рівняння динаміки системи є функціями часу.

Реакція стаціонарної системи на одне і те ж збурення не залежить від моменту, коли збурення відбулося. Для нестаціонарних систем реакція системи змінюється з часом.

VIII. За точністю керування:

- статичні;

- астатичні.

Основною із ознак даних систем є вигляд регулювальної характеристики, що показує залежність регульованої величини в статичному положенні від витрат робочого середовища.

Статичною САК називають систему, в якій регульована величина при зміні зовнішніх збурень на об'єкті, змінюючись в деяких допустимих межах, після закінчення перехідного процесу залежно від нинішнього збурення має різні значення.

Регулювальна характеристика в загальному випадку має вигляд

у = С + Δ(х), (2.2)

де С — середнє значення регульованої величини х; Δ(х) — функція збурення, яка визначає відхилення регульованої величини від її середнього значення в межах зони регулювання.

Необхідна умова якісного регулювання С >> Δ (х).

Астатичною САК називають систему, в якій регульована величина при зміні зовнішніх збурень після завершення перехідного процесу набуває строго сталого значення при різних величинах зовнішніх збурень.

Як приклад розглянемо астатичну (рис. 2.8, а) і статичну (рис. 2.9, а) САР рівня Н деякого робочого середовища (рідини) Q.

Завданням і статичної, і астатичної систем є підтримання сталого ріння Н (стабілізація) в резервуарі при зміні величини Q,.

Якщо при астатичній CAК витрати Q, збільшаться, то у зв'язку з по­чатковим зменшенням рівня Н поплавок П переміститься вниз, що призведе до відповідного переміщення повзунка потенціометра ПТ відносно його початкового положення 0. При цьому на якірному колі двигуна Д виникне напруга U відповідної полярності. Завдяки цьому двигун переміщуватиме регулюючий орган системи РО, забезпечуючи зростання надходження кількості рідини Q2 і рівня Н. Регулюючий орган переміщуватиметься доти, доки напруга на якірному колі не буде дорівнювати нулю, що можливо тільки при значенні рівня, який дорівнює заданому: Н = Нз при умові рівності витрат і надходження рідини Q₁ = Q₂ = Q.

Згідно з викладеним вище в астатичній системі можливе лише одне положення рівноваги при значенні регульованої величини Н = Нз, яка досягається в статичному стані при різних значеннях витрат робочого середовища Q.

Регулювальна характеристика Н = f(Q) (рис. 2.8, б) астатичної системи є горизонтальна пряма.

Якщо знехтувати нечутливістю елементів системи, то астатична САР в принципі може підтримувати регульовану величину після завершення перехідного процесу на заданому рівні без будь-яких відхилень.

У статичній CAP (рис. 2. 9, а) при збільшенні витрат (Q1 > Q2) рівень Н і поплавок П будуть переміщуватись вниз. Завдяки цьому регулюючий орган РО забезпечить збільшення надходження робочого середовища Q2.

Нового стану рівноваги буде досягнуто при Q1 = Q2 = Q для нового ріння Н, меншого від початкового.

Рис. 2.8. Астатична САК

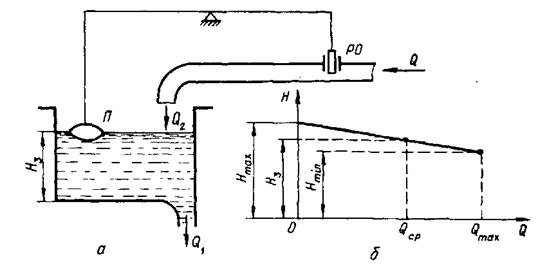
Рис. 2.9. Статична САК

Таким чином, статичні CAP не можуть забезпечувати підтримку регульованої величини на строго сталому рівні. Отже, можливі відхилення регульованої величини від заданого рівня Нз залежно від витрат робочого середовища. Регулювальна характеристика статичної САР після завершення перехідного процесу (статична характеристика статичної CAP) є похила пряма (рис. 2. 9, б).

Точність підтримання заданого значення регульованої величини в Статичних системах визначається коефіцієнтом нерівномірності або статизмом δ.

У даному випадку

(2.3)

Величину статизму іноді визначають як відношення відхилення ре­гульованої величини до її максимального значення:

У відносно грубих CAP величина статизму може становити 10—20 %.

В астатичних системах залежно від витрат робочого середовища після завершення перехідного процесу регулюючий орган також може приймати різне положення, але при одному й тому ж значенні регульованої величини.

Для технічної реалізації цієї особливості в астатичних CAP повинні мати так звані астатичні ланки, рухомий елемент яких при відсутності збурення може займати довільне положення. Такою ланкою системи в розглянутому прикладі є двигун постійного струму, якір якого може займати довільне положення при відсутності напруги на якірній обмотці двигуна.

ІХ. Залежно від наявності додаткового джерела енергії:

- прямої дії;

- непрямої дії.

САК прямої дії не мають додаткових джерел енергії та підсилювачів потужності в системі регулювання.

В системах прямої дії вимірювальний елемент самостійно діє на регулюючий орган. Так, на рис. 2.10 показано систему прямої дії регулювання швидкості. Вимірювальний елемент BE, який контролює швидкість обертів деякого об'єкта О, самостійно діє на керуючий орган, який змінює кількість енергоносія Q, що надходить в об'єкт керування. Якщо швидкість обертання ω збільшується, то кулі К1 і К2 під дією відцентрової сили переміщуються вгору, що призводить до переміщення муфти М та регулюючого органу РО. Завдяки цьому зменшуються надходження енергоносія Q і швидкість обертання об'єкта ω.

Основною перевагою систем прямої дії є простота і надійність, недоліком — необхідність мати потужний і, внаслідок цього, малочутливий, досить інерційний вимірювальний елемент, який може безпосередньо переміщувати керуючий (регулюючий) орган об'єкта. При цьому низькій чутливості вимірювального елемента відповідає мала точність керування, а значна інерційність негативно впливає на динамічні властивості системи.

САК непрямої дії містять підсилювачі потужності і споживають енергію для здійснення керування від зовнішніх джерел.

В системах непрямої дії вихідний сигнал вимірювального елемента підсилюється за допомогою підсилювача. На рис. 2. 11 показано САК непрямої дії швидкості об'єкта. В цій системі муфта М вимірювального елемента діє на золотник 3 гідропідсилювача ГП. Золотник, виходячи з нейтрального положення, як показано на рисунку, забезпечує надходження масла QM у верхню порожнину циліндра гідропідсилювача, що веде до відповідного переміщення поршня П, регулюючого органу РО і швидкості ω. Перевагою систем непрямої дії є більша точність і, часто, кращі динамічні властивості, що зумовлює їх широке застосування на практиці.

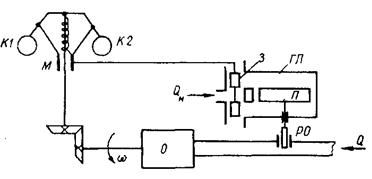
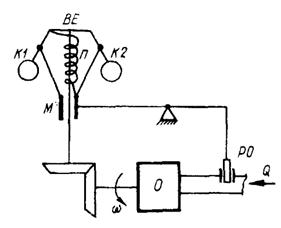
Рис. 2.10. САК непрямої дії Рис. 2.11. САК прямої дії

Х. За способом налаштування та реакцією системи на зміну зовнішніх умов:

- неадаптивні;

- адаптивні системи.

Адаптивними називаються системи, які автоматично змінюють значення своїх параметрів або структуру при непередбачених змінах зовнішніх умов, щоб зберігати задану якість її роботи.

Адаптивні системи зі зміною значень параметрів називають системами із самонастроюванням, а системи зі зміною структури - системами із самоорганізацією.

Такі САК використовуються для керування об’єктами властивості, чи умови експлуатації яких недостатньо відомі або суттєво непостійні, наприклад, САК апаратами, які спускаються на віддалені планети сонячної системи. Ці системи найбільш досконалі.

Не адаптивні системи здатності пристосовуватись до зміни зовнішніх умов не мають. У них зміна параметрів з метою забезпечення оптимальності процесу регулювання, або відсутня, або її здійснює людина.

Дата добавления: 2014-12-25