Адсорбция

Как было показано выше, в результате взаимодействия атомов потока с поверхностью и протекающих при этом процессов энергообмена определенная их часть адсорбируется. При этом плотность адсорбированных атомов n_а, ат./м², зависит от плотности потока атомов j, ат./(м²с), взаимодействующих с поверхностью, и определяется вероятностью десорбции атомов: Ŵ= n_а/t_а,, где t_а=t_оexp(E_а/kT) (2.1а) – время жизни в адсорбированном состоянии, t_о =10^-13…10^-12с; E_а – энергия связи с поверхностью; k – постоянная Больцмана. Тогда изменение плотности адсорбированных атомов за дифференциальное малое время dt: dn_а= jdt-n_аdt/t_a (2.1б). Уравнение (2.1) составлено на основании закона сохранения массы: количество адсорбированных атомов равно разности числа атомов jdt, поступающих на поверхность за время dt, и атомов, перешедших за это время обратно в газовую фазу.

Решением дифференциального уравнения (2.1) при начальных условиях (t=0 и n_a =0) является выражение: 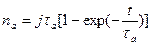(2.2). Для начальных стадий осаждения (t<<τ_a) можно принять, что 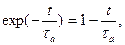тогда на основании (2.2) получим: n_a=jt. Таким образом, при малых временах осаждения наблюдается линейное возрастание плотности адсорбированных атомов в процессе осаждения.

На поздних стадиях роста, при t>>τ_a из (2.2) получим n_a=jτ_a. Следовательно, при таких режимах адсорбционная фаза характеризуется равновесной плотностью, зависящей только от j и t_{а .} При прекращении поступления атомов на поверхность происходит их десорбция, и через время t_а они все покинут поверхность.

2.1.3. Поверхностная диффузия.

Адсорбированный атом совершает хаотическое или направленное движение в поверхностном слое (само- или взаимодифузию соответственно) в зависимости от отсутствия или наличия градиента концентрации или химического потенциала. В зависимости условий формирования покрытий в процессе диффузии атом может либо присоединиться к зародышу конденсированной фазы (устойчивой частице осаждаемого материала), т.е. участвовать в формировании покрытия, либо же через некоторое время t, равное времени жизни в адсорбированном состоянии t_а, перейти обратно в газовую фазу, т.е. в десорбированное состояние (Рис.2.7).

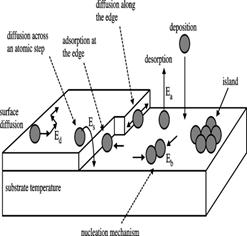
Рис. 2.7. Схема протекающих процессов при адсорбции атомов (substrate temperature –подложка при заданной температуре; diffusion across an atomic step – диффузия поперек атомной ступени; adsorption at the edge – адсорбция на краю ступени; diffusion along the edge - диффузия вдоль атомной ступени; desorption - десорбция; deposition - осаждение; island – стабильный зародыш покрытия (островковая структура); nucleation mechanism – механизм нуклеации)

Поверхностная диффузия характеризуется длиной диффузионного пробега Х=(2Dt_а )^1/2, которая равна расстоянию, проходимому атомом на поверхности за время его жизни в адсорбированном состоянии. С учетом уравнения 2.1а Х= 2аexp[(Е_а – Е_d)/2kT], где а – расстояние между соседними адсорбционными узлами поверхности; D– коэффициент поверхностной диффузии – коэффициент пропорциональности в линейном законе Фика , где j_a- поток дффундирующих атомов в адсорбционном слое, dn/dx – градиент их концентрации или плотности слоя; Е_а и Е_d – энергия активации процессов адсорбции и поверхностной диффузии соответственно; k - постоянная Больцмана).

Дата добавления: 2014-12-25