
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Зародышеобразование адсорбционной фазы и рост зародышей
|
|
|
|
2.2.1. Классическая термодинамическая теория гомогенного зарождения новой фазы в первоначальной фазе.
Обобщенная термодинамическая теория гомогенного зарождения новой фазы при конденсации пара или кристаллизации жидкости, развитая Дж. Гиббсом (1876-78 г) и М. Фольмером (1939 г), базируется на том, что при температуре ниже, чем температура равновесного фазового перехода первоначальной (предшествующей) фазы в новую (Тфп=ΔНфп/ΔSфп, где ΔНфп и ΔSфп – изменение энтальпии и энтропии при фазовом переходе), система сохраняет равновесное стабильное, так называемое метастабильное состояние, первоначально фазы. Хотя такое состояние энергетически менее выгодно, чем состояние новой фазы при этих условиях, так как первоначальная фазы обладает большей свободной энергией, но она не может перейти в более выгодное состояние новой фазы из-за необходимости преодоления энергетического барьера ее образования. Возникающие в метастабильном состоянии термодинамически обусловленные флуктуации плотности в виде объемных сферических частиц, структура которых соответствует структуре новой фазы, уменьшают объемную свободную энергию системы тем больше, чем больше их размер. С другой стороны, увеличение размера флуктуаций плотности сопровождается увеличением свободной энергии, связанной с образованием поверхности раздела первоначальная фаза - новая фаза. При постоянных давлении и температуре общее изменение свободной энергии (термодинамического потенциала) Гиббса 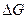 при изменении радиуса флуктуации равно:
при изменении радиуса флуктуации равно:  , где s – поверхность частицы, γ - удельная свободная поверхностная (межфазная) энергия границы раздела первоначальная фаза - новая фаза; n – число молей вещества в частице новой фазы, Vm - его мольный объем. Зависимость ΔG(r) имеет максимум при r=rк (рис. 2.8, кривые 2,3), которому соответствует состояние неустойчивого равновесия между зародышем и исходной фазой.
, где s – поверхность частицы, γ - удельная свободная поверхностная (межфазная) энергия границы раздела первоначальная фаза - новая фаза; n – число молей вещества в частице новой фазы, Vm - его мольный объем. Зависимость ΔG(r) имеет максимум при r=rк (рис. 2.8, кривые 2,3), которому соответствует состояние неустойчивого равновесия между зародышем и исходной фазой.
|
|
|
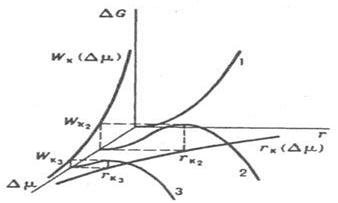
Рис. 2.8. Влияние переохлаждения (удаления от Тфп в метастабильной области), т.е. увеличения Δμ, на зависимость ΔG(r) частицы новой фазы и работу ее образования Wк (rк - радиус критического зародыша; кривая 1 соответствует Δμ = 0, кривые 2 и 3 соответствуют возрастающим значениям Δμ).
При r=rк химический потенциал вещества в объемном зародыше новой фазы, повышенный за счет действия поверхностной энергии и капиллярного давления Δрγ = 2γ/r, равен его химическому потенциалу в первоначальной фазе. В частицах размером, меньшим чем rк, химический потенциал вещества выше, чем в первоначальной фазе, и такие частицы стремятся уменьшить свой размер, т.е. флуктуации исчезают. Частицы, у которых r>rк, имеют более низкий химический потенциал, чем в первоначальной фазе, и могут неограниченно расти за счет перехода вещества в них из первоначальной фазы. Частица с радиусом rк (rк =2γVm/Δμ) называется критическим зародышем. Выражение для критического размера зародыша получается из условия максимума ΔG(r) при r=rк: 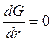 . После дифференцирования ΔG(r) получается уравнение:
. После дифференцирования ΔG(r) получается уравнение: 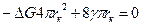 , решение которого дает искомое выражение для rк.
, решение которого дает искомое выражение для rк.
Таким образом, для возникновения объемного критического зародыша необходимо затратить работу Wк, равную (по Гиббсу) одной трети его поверхностной энергии: 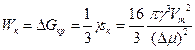 , где sк - поверхность критического зародыша. Величину Wк можно рассматривать как высоту энергетического барьера при зарождении новой фазы
, где sк - поверхность критического зародыша. Величину Wк можно рассматривать как высоту энергетического барьера при зарождении новой фазы  . Его преодоление осуществляется флуктуационным путем. Чем больше переохлаждение (удаление от Тфп в метастабильной области), так называемая глубина внедрения в метастабильную область (Δμ), тем ниже высота энергетического барьера Wк (см. Рис.2.8).
. Его преодоление осуществляется флуктуационным путем. Чем больше переохлаждение (удаление от Тфп в метастабильной области), так называемая глубина внедрения в метастабильную область (Δμ), тем ниже высота энергетического барьера Wк (см. Рис.2.8).
|
|
|
При гомогенном образовании несферических (анизотропных кристаллических) зародышей их форма определяется условием Гиббса-Кюри о минимуме поверхностной энергии зародыша γisi, где γi и si – соответственно, удельные свободные поверхностные энергии и площади i-ты х граней кристалла. Этому условию отвечает соотношение Вульфа: γi/hi = const, где hi - расстояние i -й грани от центра кристалла. Зависимость ΔG(hi) при образовании кристаллических зародышей сходна с выражением для ΔG(r) сферических зародышей, но численные коэффициенты оказываются иными. Часто выражение ΔG(r) применяют и при рассмотрении образования кристаллических зародышей, подразумевая под величиной γ некоторое усредненное (эффективное) значение удельной поверхностной энергии зародыша.
2.2.2. Классическая термодинамическая теория гетерогенного зарождения новой фазы в первоначальной фазе.
В соответствие с теорией Гиббса-Фольмера работа образования объемного критического зародыша может уменьшаться при образовании зародыша на смачиваемой им твердой поверхности, т.е. при так называемом гетерогенном зарождении новой фазы (Рис. 2.9).

Рис. 2.9. Гетерогенное образование объемного зародыша на плоской поверхности (θ - краевой угол смачивания).
Если при этом радиус кривизны поверхности критического зародыша rк остается неизменным, то соотношение работ гетерогенного (Wкгет) и гомогенного (Wкгом) образований критического зародышей определяется углом смачивания: 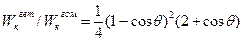 .
.
Таким образом, работа образования объемного критического зародыша при гетерогенном зарождении новой фазы всегда ниже, чем при гомогенном, и меняется от Wкгом до 0 при изменении θ от 180° до 0°. Зарождение новой фазы еще более облегчается на дефектах структуры поверхности.
Возникновение двухмерных (плоских, остовковых) зародышей при кристаллизации на поверхности как образование новых атомных или молекулярных плоскостей с высотой а, равной межплоскостному расстоянию в классической термодинамической теории рассматривается как особый вид гомогенного зарождения новой фазы и описывается аналогично зарождению трехмерных (объемных) зародышей: для зародышей квадратной формы с длиной ребра l и межплоскостным расстоянием а зависимость ΔG(al) описывается аналогично зависимости ΔG(r): 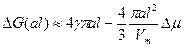 При этом критический размер зародыша lк=2γVm/Δμ, а работа его образования Wк = 4γ2аVm/Δμ.
При этом критический размер зародыша lк=2γVm/Δμ, а работа его образования Wк = 4γ2аVm/Δμ.
|
|
|
При образовании двух- или трехмерных кристаллических зародышей в адсорбционной фазе важное значение имеет структурное соответствие зародыша новой фазы и поверхности подложки, на которой он образуется. Выделение кристаллической фазы на подложке с близкими параметрами их кристаллической структуры называется эпитаксиальным ростом. При зарождении новой фазы на кристаллической поверхности при эпитаксиальном росте необходимо учитывать энергию упругих напряжений, возникающих из-за структурного различия исходной фазы и поверхности подложки: чем больше это различие, тем больше напряжения.
2.2.3. Классическая кинетическая теория зарождения новой фазы.
Теоретическое описание кинетики зарождения новой фазы (нуклеации) является более сложной проблемой, чем определение термодинамических условий образования и роста равновесных зародышей. Рассмотрению кинетических теории нуклеации посвящены многие работы, но удовлетворительного результата, особенно для зарождения на плоскости до сих пор нет. При этом возникновение способного к дальнейшему росту зародыша с размером, большим критического, также как в классической термодинамической теории рассматривается как флуктуационный процесс образования термодинамически невыгодного микросостояния, т. е. состояния, которому отвечает увеличение свободной энергии системы из-за избыточной поверхностной свободной энергии. Если величина Δμ мала (при малом углублении в метастабильную область), в системе возникает равновесное распределение флуктуаций по размерам, которое может быть описано равновесной функцией распределения: f0 (r) = N1ехр(—ΔG(r)/kT), где k - постоянная Больцмана, N1 - обычно рассматривается как число мест, которые может занимать центр флуктуации: оно приближенно равно числу атомов или молекул в единице объема системы (иногда учитываются некоторые дополнительные энтропийные эффекты). Поскольку при малом Δμ величина Wк = ΔG(rк) велика (см. рис. 2.8), вероятность образования критических зародышей пренебрежимо мала, а значит невозможно образование и термодинамически выгодных крупных зародышей, для которых ΔG(r)<0. При этом функция распределения f0(r) относится только к докритическим зародышам. При достаточно высоком Δμ и малом Wк появление критических зародышей становится достаточно вероятным, а после присоединения к ним одного или нескольких атомов его рост становится необратимым. Можно сказать, что в такой системе случайные процессы увеличения и уменьшения размеров зародышей ведут к их направленной "диффузии вдоль оси размеров" к закритическому состоянию. При этом устанавливается некоторая стационарная функция распределения зародышей по размерам f(r), отличающаяся от равновесной f0(r). Частота образования закритических зародышей I, т.е. их число, возникающее в единицу времени в единице объема системы, описывается выражением:  . В этом выражении z=f(rк)/f0(rк) - "неравновесный фактор", который пропорционален (γ/kT)1/2. "Кинетический фактор" ω описывает скорость роста критических зародыша. При этом обратную величину ω (1/ω) можно рассматривать как время жизни критического зародыша, т. е. время присоединения к нему еще одного атома, переводящего его в закритическое состояние. Выражения для ω сложны и зависят от типа фазового перехода. Так, для случая конденсации пара:
. В этом выражении z=f(rк)/f0(rк) - "неравновесный фактор", который пропорционален (γ/kT)1/2. "Кинетический фактор" ω описывает скорость роста критических зародыша. При этом обратную величину ω (1/ω) можно рассматривать как время жизни критического зародыша, т. е. время присоединения к нему еще одного атома, переводящего его в закритическое состояние. Выражения для ω сложны и зависят от типа фазового перехода. Так, для случая конденсации пара:  , где sк - поверхность критического зародыша, р – давление пара, М – молекулярная масса, NA - число Авогадро).
, где sк - поверхность критического зародыша, р – давление пара, М – молекулярная масса, NA - число Авогадро).
|
|
|
Существенная зависимость частоты образования зародышей I от Δμ приводит к тому, что гомогенное зарождение новой фазы возможно только при достаточно высоких значениях Δμ, после чего происходит резкий рост I с увеличением Δμ. Дальнейший рост сверхкритических зародышей может определяться скоростью подвода (диффузией) вещества из объема исходной фазы, скоростью отвода тепла, выделяющегося при фазовом переходе, или скоростью пристраивания атомов к поверхности растущего зародыша. Поскольку Δμ снижается вблизи растущей частицы, вероятность образования новых зародышей в системе со временем уменьшается. Если скорость образования новых зародышей велика, а скорость их роста мала, образуется высокодисперсная система. Близкая к монодисперсной система может быть получена при длительном поддерживании в системе пересыщения (переохлаждения) за счет медленно протекающей химической реакции или при введении большого числа искусственных зародышей, например, частиц ТiO2. При выращивании монокристаллов в системе постоянно поддерживают заданное пересыщение и отложение вещества ведут на затравках.
Дальнейшая эволюция дисперсной системы, образующейся при зарождении новой фазы, может быть связана с протеканием процессов коагуляции и переноса вещества от малых частиц к более крупным при созревании Оствальда (см. раздел 2.3). Перенос обусловлен различием химического потенциала вещества в частицах разных размеров (эффект Гиббса-Томсона).
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 1288; Нарушение авторских прав?; Мы поможем в написании вашей работы!