Правило знаков для продольной силы N

Если внешняя сила F направлена от сечения, то сила N –положительная, если внешняя сила F направлена к сечения, то сила N –отрицательная.

При решении задач, силу N будем считать положительной, и направлять её от сечения. Если при решении задачи, сила N будет отрицательной, это означает, что она направлена к сечении.

Если продольная сила направлена от сечения, то брус растянут. Растяжение считается положительной деформацией.

Если продольная сила направлена к сечения, то брус сжат. Сжатие считается отрицательной деформацией.

Изменение продольный силы по длине бруса удобно представлять в виде диаграммы, называемой эпюрой продольных сил.

Ось эпюры параллельна продольной силе. Нулевая линия проводится тонкой линией. Значения сил откладываются от оси, вверх – положительные, вниз – отрицательные. В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

Эпюра штрихуется тонкими линиями, перпендикулярными оси. Для наглядности на эпюрах N и знаками «+» и «—» отмечаются положительные и отрицательные значения участков эпюр.

При растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле ,

где 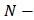продольная сила; A- площадь поперечного сечения. Очевидно, что при растяжении и сжатии форма сечения на напряжение не влияет.

Во всех сечениях бруса напряжения распределены равномерно и что в сечении, где к брусу приложена вдоль оси сосредоточенная сила, значения продоль­ной силы и напряжений меняются скачкообразно.

Пример. Построить эпюры продольных сил и нор­мальных напряжений для сту­пенчатого бруса.

Решение.

1. Разобьем брус на участки и пронумеруем их, как показано на рисунке.

2. Для построения эпюры продольных сил N под рисунком бруса проводим ось эпюры, параллельную оси бруса, и линиями ограничиваем его участки.

3. Приступим к построению эпюры N.Применяя метод сечений, устанавли­ваем, что во всех поперечных сечениях первого участка действует продольная си . Откладываем вверх от оси эпюры величину и произвольном масштабе и проводим прямую, параллельную оси эпюры. В точке С бруса приложена . Применяя метод сечений, устанавливаем, что во всех поперечных сечениях второго и третьего участков действуем продольная сил 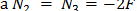и эпюра N будет горизонтальной линией, расположенной на 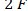единиц ниже оси эпюры. Очевидно, что значение ординаты эпюры продольных сил под заделкой равно реакции заделки.

4. Для построения эпюры определим нормальные напряжения на участках бруса, беря отношение значения продольной силы (из опоры 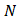) к площади поперечного сечения. Тогда на первом участке нормальные напряжения будут равны , на втором - , на третьем - .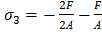

5. Правила построения эпюры те же, что и для эпюры N, включая и правило знаков. В пределах каждою из участков напряжения постоянны, поэтому эпюра на каждом участке прямая, параллельная оси.

Дата добавления: 2014-12-25