Тема 23. Спрос на ресурсы и их эффективное использование

Тема 22. Предприятие в условиях монополистической конкуренции и олигополии.

Задача 22.1. Проанализировав график, посчитайте максимальную прибыль предприятия работающего на рыке монополистической конкуренции.

а. 650

б. 195

в. 375

г. 50

Комментарий к заданию 5. Максимальная прибыль предприятия, работающего на рынке монополистической конкуренции, будет соответствовать площади четырехугольника образованного пересечением перпендикуляра, проведенного через точку (К) где MR=MC, с кривой средних общих издержек (ATC) и кривой спроса (D). Таким образом P_max = = (30-15)∙25=375. Ответ – в.

Задача 23.1. Производственная функция имеет вид Y=K∙L. Если общий объем затрат не должен превышать 30, цена труда равна 4, цена капитала - 5, то при какой комбинации труда и капитала будет достигнут максимальный выпуск?

а. 3.75 и 3

б. 2.52 и 2

в. 3.25 и 4

Комментарий к заданию 4. Искомые значения труда и капитала являются координатами точки касания изокванты Y=L∙K (при некотором Y) и изокосты 4L+5K=30. Общие точки этих двух кривых удовлетворяют системе . Отсюда К=(30-4L)/5=6-0.8L и тогда Y=L(6-0,8L)=6L-0,8L². Найдем максимум Y по L: 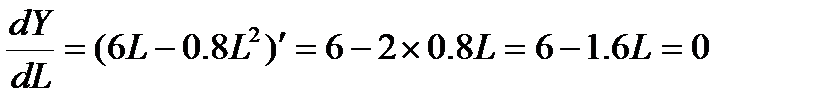, т.е. L=3.75. Подставим значение L в уравнение 4L+5K=30; 4∙3.75+5K =30, тогда K=3 и максимальный выпуск равен 11.25 (3 *3,75) Ответ – а.

Задача 23.2. Производственная функция фирмы имеет вид Y=100K∙L. Цена труда составляет 30, а капитала - 120. Чему равны средние издержки производства 100 единиц продукции, если фирма выбирает самый дешевый способ производства?

а. 1.2

б. 1.5

в. 1.4

омментарий к заданию 5. Минимальные издержки C соответствуют точке касания изокванты 100K∙L=100 и изокосты 30L+120K=C. Общие точки этих двух кривых удовлетворяют системе 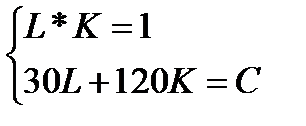. Отсюда К=1/L соответственно C=30L+120/L. Найдем минимум C по L 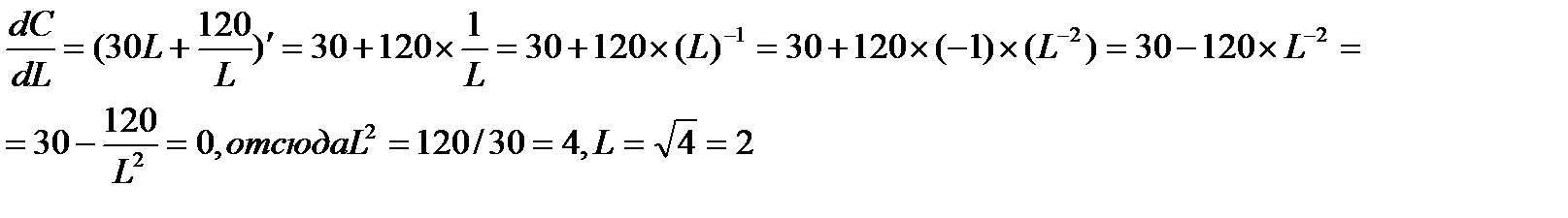, т.е. L=2. Тогда K∙2=1; К=0,5. Для получения минимальных издержек подставим значение K и L во второе уравнение системы 30∙2+120∙0.5=120. Средние издержки определяются как издержки, приходящиеся на единицу выпуска, т.е. 120/100=1,2. Ответ – а.

Задача 23.3. Совершенно конкурентное предприятие использует ресурсы X и Y, покупая их также на совершенно конкурентном рынке по ценам: Ц_х=120 руб., Ц_у=90 руб. Если предельный продукт ресурса Х равен 20 ед., а ресурса Y- 15 ед., то при какой цене на товар предприятие будет максимизировать прибыль?

а. 6 руб.

б. 7 руб.

в. 8 руб.

К

Комментарии к заданию 6. Цена на ресурс X (Ц_х) равна 120 руб. и цена ресурса Y (Ц_у) равна 90 руб.; предельный продукт ресурса х (ПП_x) равен 20 и предельный продукт у (ПП_у) равен 15. Для нахождения цены товара, максимизирующего прибыль предприятия при минимизации издержек, используются следующие отношения: 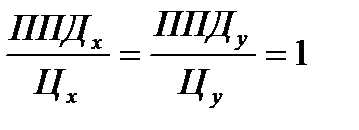, где

ППД — (предельный продукт в денежном выражении или предельный доход ресурса) = ПП (предельный продукт) * Ц.

Подставив в предыдущее равенство значение ППД, получим: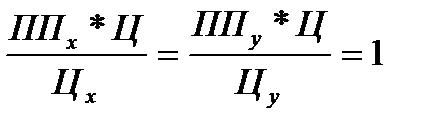

Из данного уравнения можно найти цену, при которой предприятие будет максимизировать свою прибыль: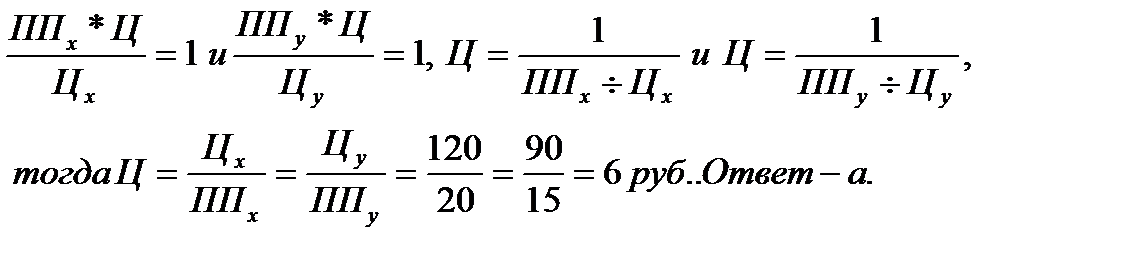

Дата добавления: 2014-12-25