Корреляционный анализ. Метод наименьших квадратов

Метод наименьших квадратов

При проведения опыта, целью которого является определение зависимости одной физической величины Y от другой X, неизбежны погрешности измерения. Поэтому возникает задача: по имеющимся экспериментальным точкам (y_i x_i) наилучшим образом воспроизвести искомую зависимость Y=f(X). Для решения подобных задач часто применяют метод наименьших квадратов, при использовании которого требование наилучшего (в смысле наиболее вероятного) согласования зависимости Y = f(X) с данными эксперимента сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей кривой обращалась в минимум:

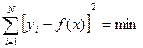
где y_i и x_i - экспериментальные значения переменных в i-м опыте; N- число опытов.

Во многих задачах требуется не только установить зависимость изучаемой случайной величины Y от одной или нескольких других случайных величин, но и оценить тесноту этой зависимости. Известно, что две случайные величины X и Y могут быть связаны функциональной или статистической зависимостями. В последнем случае изменение одной из величин влечет изменение распределения другой. В частности, если статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой, то она называется корреляционной (от лат. - взаимосвязь, взаимозависимость).

Дата добавления: 2014-12-25