Структура СПРК

Ку.

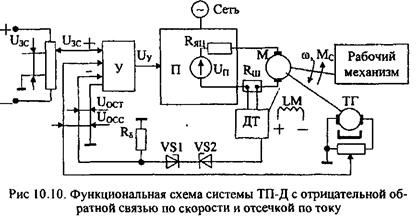
Обычно по условиям эксплуатации технологических устано­вок и условиям коммутации на коллекторе двигателя необходимо ограничивать максимальный момент, развиваемый двигателем, на уровне (2+3)М„. С этой целью в замкнутых системах электро­привода применяется задержанная отрицательная обратная связь по току якоря, называемая токовой отсечкой. Функциональная схема электропривода постоянного тока с отрицательной обрат­ной связью по скорости и токовой отсечкой приведена на рис. 10.10. Токовая отсечка в этой схеме реализована на стабили­тронах VS1 и VS2. Уравнения цепи обратной связи по току будет:

lame - ток якоря, при превышении которого вступает в дейст­вие отрицательная обратная связь по току;

и_ест - сигнал (напряжение) отрицательной обратной связи по току.

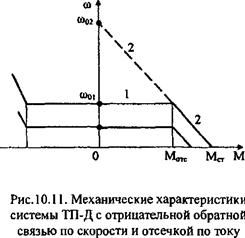
В результате со­вместного действия отрицательных об­ратных связей по скорости и току фор­мируется механиче­ская характеристика (см. рис. 10.11), кото­рая состоит из двух участков: рабочего(1) с высокой жестко­стью и участка (2) ограничения момента. На рабочем участке, пока не действует отрицательная об­ратная связь по току, механические харак­теристики описываются уравнением (10.4). При 1_я>1_отс работа электропривода может быть описана следующими уравнениями

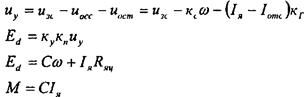
В результате решения этой системы уравнении относительно со получим уравнение механической характеристики для второго участка

Первые два слагаемых уравнения (10.6) определяют ско­рость идеального холостого хода механической характеристики для второго участка

Жесткость механической характеристики на втором участке будет

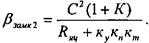
-З.д.с. преобразователя U_d при работе двигателя с замкнутой системой управления не остается постоянной, а изменяется в со­ответствии с уравнением

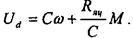
На рабочем участке механической характеристики скорость примерно постоянна. С увеличением нагрузки на валу двигателя U_d возрастает. После перехода на второй участок и дальнейшем повышении нагрузки скорость снижается до нуля, наступает режим стопорения и уменьшается до величины

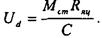
Таким образом, для формирования желаемой механической характеристики преобразователь должен иметь необходимый за­пас по величине E_d в соответствии с соотношением

В этой случае жесткость верхней механической
характеристики будет постоянной при всех нагрузках

вплоть до М_ош.

В связи с расширением использования полупроводниковой техники управ­ления и созданием унифицированных блочных систем регуляторов (УБСР), пред­назначенных для управления электроприводами, практический интерес представ­ляет последовательная коррекция контуров регулирования. При подчиненном регулировании координат система электропривода раз­деляется на группы звеньев, в каждой из которых, как правило, имеется только одна большая постоянная времени. Каждая из таких групп звеньев включается в контур регулирования со своим регулятором и обратной связью. В результате система получается многоконтурной, причем каждый последующий контур охва­тывает предыдущий. Выходные величины регуляторов внешних контуров регу­лирования оказываются входными для внутренних контуров регулирования.

Требуемые показатели качества регулирования в оптимизированном кон­туре (колебательность и перерегулирование) обеспечиваются выбором отношения постоянных времени а, а быстродействие определяется только величиной суммарной некомпенсированной постоянной времени Т_μ.

где — суммарная некомпенсированная постоянная времени контура регулирования.

а=Т₀ /Т_μ=2

При а=2 обеспечивается время регулирования, то есть когда регулируемая переменная первый раз достигает установившейся величины, t_p1 = 4,7 Т_μ при пе­ререгулировании меньшем 5 %. Полученный оптимум принято называть «техни­ческим» или «модульным».

Настройка на модульный оптимум обеспечивает наилучшие показатели регулирования по каналу управления, но не обеспечивает быстрой реакции системы на возмущение. Таким образом, для компенсации влияний возмущений регулятор должен быть настроен на «Симметричный Оптимум» (а=Т₀/Т_μ=4). В этом случи регулируемая переменная первый раз достигает установившейся величины, t_p1 = 3,1 Т_μ

11. Синтез (настройка) регуляторов тока и скорости на «МО» в системах ТП-Д, ТВ-Г-Д (Т_ТВ≠0).

Требуемые показатели качества регулирования в оптимизированном кон­туре (колебательность и перерегулирование) обеспечиваются выбором отношения постоянных времени а, а быстродействие определяется только величиной суммарной некомпенсированной постоянной времени Т_μ.

где — суммарная некомпенсированная постоянная времени контура регулирования.

а=Т₀ /Т_μ=2

При а=2 обеспечивается время регулирования, то есть когда регулируемая переменная первый раз достигает установившейся величины, t_p1 = 4,7 Т_μ при пе­ререгулировании меньшем 5 %. Полученный оптимум принято называть «техни­ческим» или «модульным».

Настройка на модульный оптимум обеспечивает наилучшие показатели регулирования по каналу управления, но не обеспечивает быстрой реакции системы на возмущение. Таким образом, для компенсации влияний возмущений регулятор должен быть настроен на «Симметричный Оптимум» (а=Т₀/Т_μ=4). В этом случи регулируемая переменная первый раз достигает установившейся величины, t_p1 = 3,1 Т_μ

Синтез регулятора тока:

При синтезе регулятора тока пренебрегаем влиянием внутренней обратной связи по ЭДС двигателя, что сказывается на точности регулирования тока, незна­чительно влияет на динамические показатели, но существенно упрощается синтез регулятора. При этом передаточная функция объекта регулирования КРТЯ примет вид:

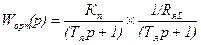
Желаемая передаточная функция разомкнутого КРТЯ:

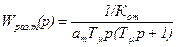
Передаточная функция регулятора тока:

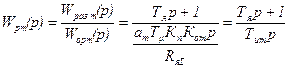
то есть получена передаточная функция ПИ-регулятора:

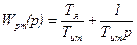
с постоянной времени интегрирования:

и коэфф. усиления пропорциональной части:

K_ут=Т_я /Т_ит

Параметры элементов и передаточной функции регулятора тока связаны следующими соотношениями:

Т_ит=R_зтС_ост

К_ут=R_ост /R_зт

Т_я=R_остС_ост

Синтез регулятора скорости:

В соответствии с рис. 3 объект регулирования скорости состоит из замкну­того контура регулирования тока якоря и механического звена электропривода и имеет передаточную функцию:

где Т_м=(R_яΣ×J_Σ)/c² — электромеханическая постоянная времени электропривода;

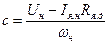— постоянная двигателя, В×с;

R_я.д — активное сопротивление якорной цепи двигателя, Ом.

Т_м=(3,3×0,12)/0,77²=0,67 с

Преобразуя передаточную функцию объекта регулирования скорости, пренебрегая членом, содержащим р² вследствие малости его коэффициента, в передаточной функции замкнутого КРТЯ:

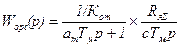
Желаемая передаточная функция разомкнутого контура регулирования скорости имеет вид:

,

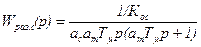где а_с=Т_ос /Т_μс — отношение постоянных времени в оптимизированном КРС.

Передаточная функция регулятора скорости:

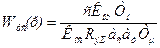
Таким образом, получен пропорциональный регулятор скорости с коэфф. передачи:

,

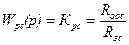где R_оос и R_зс — соответственно сопротивления резисторов цепи обратной связи и задающего входа усилителя (рис. 6).

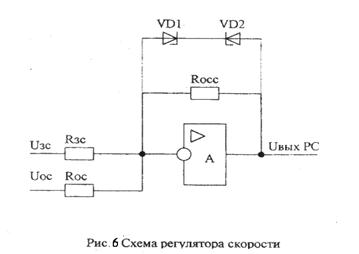
Коэфф. обратной связи приводится к цепи задающего сигнала:

К_ос=К_BRR_зс /R_ос,

где К_BR=U_BR /ω_дв — передаточный коэфф. тахогенератора.

Для определения величины К_ос необходимо задаться наибольшим входным напряжением задания по скорости U_зс.max, соответствующим заданной величине скорости идеального холостого хода двигателя. Эти параметры связаны между собой следующим соотношением:

U_зс.max=K_осω₀

Уравнение статической электромеханической характеристики в системе подчиненного регулирования координат получим исходя из условия равенства напряжений задания по току якоря U_зт=(U_зс-К_осω)W_pc(p) и обратной связи U_от=К_отI_я на входе регулятора тока. Тогда

, или

,

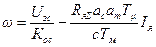а в случае настройки обоих контуров регулирования на “модульный оптимум”, то есть при а_с=а_т=а=2, выражение примет вид:

Еще раз отмечаем, что контуры регулирования в системах подчиненного регулирования координат по управляющему воздействию являются астатическими, т.е. ошибки регулирования координат равны нулю (при М_с=0 ω₀=U_зс /К_ос=const и при Е_дв=сω=0 I_стоп=U_зт.max / К_от=const).

При действии возмущающего воздействия появляется статическая ошибка регулирования по скорости:

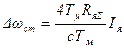
Статические электромеханические характеристики привода оптимизиро­ванного методом последовательной коррекции и настроенные на «модульный оп­тимум» приведены на рис. 8.

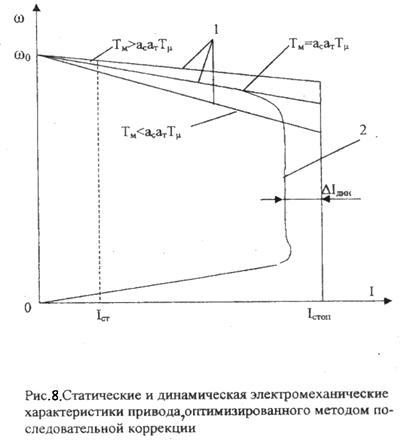
1 – статические характеристики

2 – динамическая характеристика

Дата добавления: 2014-12-25