Теоретический материал. Курс заочной формы обучения

Введение

Курс заочной формы обучения

Курс заочной формы обучения

Курс заочной формы обучения

Курс заочной формы обучения

Курс заочной формы обучения

Курс заочной формы обучения

Перевод (английский)

Курс заочной формы обучения

Перевод (английский)

Курс заочной формы обучения

Перевод (английский)

Курс заочной формы обучения

Перевод (английский)

Курс заочной формы обучения

№п/п	Ф.И.О.	Колич-во книг

ДОЛЖНИКОВ НЕТ

№п/п	Ф.И.О.	Колич-во книг

ДОЛЖНИКОВ НЕТ

№п/п	Ф.И.О.	Колич-во книг

ДОЛЖНИКОВ НЕТ

№п/п	Ф.И.О.	Колич-во книг

ДОЛЖНИКОВ НЕТ

№п/п	Ф.И.О.	Колич-во книг

ДОЛЖНИКОВ НЕТ

Язык и литература (немецкий)

№п/п	Ф.И.О.	Колич-во книг

ДОЛЖНИКОВ НЕТ

Язык и литература (немецкий)

№п/п	Ф.И.О.	Колич-во книг

ДОЛЖНИКОВ НЕТ

Язык и литература (немецкий)

№п/п	Ф.И.О.	Колич-во книг

ДОЛЖНИКОВ НЕТ

Язык и литература (немецкий)

№п/п	Ф.И.О.	Колич-во книг

ДОЛЖНИКОВ НЕТ

Язык и литература (немецкий)

№п/п	Ф.И.О.	Колич-во книг

ДОЛЖНИКОВ НЕТ

Данные методические указания составлены в соответствии с рабочей программой по дисциплине «Техническая механика» для специальности 140 «Техническая эксплуатация и ремонт электрического и электромеханического оборудования».

Методические указания содержат необходимый теоретический материал по данной теме, примеры решения задач, задания для выполнения практических и расчетно-графических работ.

Данное пособие может быть использовано студентами для самостоятельного выполнения практической части программы при отсутствии на занятиях по разным причинам.

Чистым изгибом называется деформация, при которой в поперечном сечении бруса возникает только изгибающий момент.

Деформация чистый изгиб возникает в том случае, если к прямому брусу в плоскости, проходящей через ось бруса, приложить две равные по величине и противоположные по знаку пары сил.

Поперечным изгибом называется деформация, при которой в поперечном сечении бруса возникает изгибающий момент поперечная сила.

Деформация поперечный изгиб возникает в том случае, если к прямому брусу приложены активные и реактивные силы, перпендикулярные оси бруса.

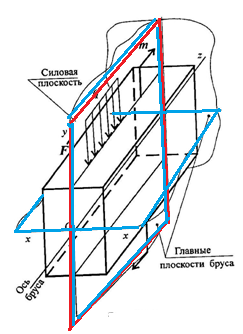Пусть брус, закрепленный справа, нагружен внешними силами и моментом.

Плоскость, в которой расположены внешние силы и моменты называется силовой плоскостью.

Если все силы лежат в одной плоскости. То изгиб называется прямым.

Плоскость, проходящая через продольную ось бруса и одну из главных центральный осей его поперечного сечения бруса, называется главной плоскостью бруса.

Если силовая плоскость совпадает с главной плоскостью бруса, изгиб называется прямым.

Для определения внутренний силовых факторов используют метод сечения.

При прямом поперечном изгибе в поперечных сечениях балки возникает два внутренних силовых фактора – поперечная сила Q_y и изгибающий момент M_x.

Поперечная сила, возникающая в произвольном поперечном сечении, численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения. .

Изгибающий момент в произвольном поперечном сечении численно равен алгебраической сумме моментов относительно центра тяжести сечения всех внешних сил, действующих справа или слева от сечение.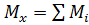

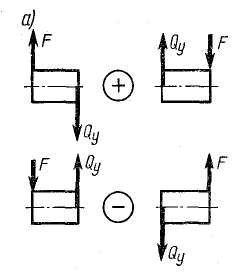
Правило знаков для силы:

· Если внешняя сила F, стремится повернуть рассматриваемую часть балки по часовой стрелки, то поперечная сила будет положительной;

· Если внешняя сила F, стремится повернуть рассматриваемую часть балки против часовой стрелки, то поперечная сила будет отрицательной (рисунок а).

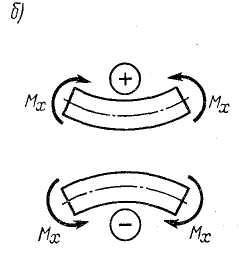
Правило знаков для момента:

· Если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент будет положительный;

· Если внешняя нагрузка стремится изогнуть балку выпуклостью вверх, то изгибающий момент будет отрицательным.

Для балок, имеющих много участков нагружения, т. е. нагруженных комбинацией нагрузок, целесообразно строить эпюры по характерным сечениям, а именно: вычислять поперечные силы и изгибающие моменты только для сечений, в которых эпюры претерпевают изменения, а затем, зная закон изменения эпюры между найденными сечениями, соединить их соответствующими линиями. К характерным относятся сечения, в которых приложены сосредоточенные силы или моменты.

Для построения эпюр необходимо запомнить следующие правила:

1. На участках, где изгибающий момент постоянен, поперечная сила равна нулю.

2. На участках, где приложена сосредоточенная сила: сила постоянна, а изгибающий момент изменяется по линейному закону, т.е. по прямой.

3. В точках приложения сосредоточенных сил на эпюре поперечных сил имеют место скачки, равные по значению силам, а на эпюре моментов - переломы, направленные навстречу силам.

4. В точках приложения пар сил на эпюре моментов возникают скачки, равные моментам пар, а эпюра Q_y не претерпевает изменения.

5. В точках, где поперечная сила равна нулю, значение момента принимает экстремальное значение - тах или тin.

6. В сечениях, где приложена сосредоточенная сила, значение поперечной силы определяется левее или правее сечений.

7. В сечениях, где приложена пара сил, значение изгибающего момента определяется правее или левее сечения.

8. Если на концах балки не приложена пара сил, то изгибающий момент равен нулю.

9. Если на концах балки не приложен внешний момент, то значение изгибающих моментов равно нулю.

10. Если на концах балки приложен внешний момент, то значение изгибающего момента равно внешнему моменту. При этом необходимо определить его знак.

11. При построении эпюры для консольной балки начало координат удобно брать на свободном конце балки, что дает возможность обойтись без определения реакций опор. В сечении соответствующем заделки, поперечная сила равна реактивной силе, а изгибающий момент – реактивному моменту.

После построению эпюры необходимо проверить, применяя следующие правила:

1. Правильность построения эпюр проверяют всегда слева на право.

2. Если Q = 0, то М_и = const.

3. Если Q > 0, то М_и - возрастает.

4. Если Q < 0, то М_и - убывает.

Дата добавления: 2014-12-25