Нормальные напряжения при чистом изгибе

Последовательность решения задачи на построение эпюр поперечных сил и изгибающих моментов

1. Освобождаем балку от опор, а действие опор заменяем реакциями опор.

2. Определяем реакции опор балки (по двум уравнениям моментов: одно – относительно левой опоры, второе – относительно правой), а затем обязательно проверить правильность решения по уравнению проекций на ось, перпендикулярную балке;

3. Определяем характерные сечения балки (сечения балки, где приложены сосредоточенные силы и моменты, включая опорные сечения).

4. Строим эпюру поперечных сил, для чего вычисляем значения поперечных сил в характерных сечениях.

5. Строим эпюру изгибающих моментов, для чего определяем значение изгибающих моментов в характерных сечениях.

При деформации изгиба:

· Поперечные прямые линии остаются прямыми, но повернуться навстречу друг другу;

· Продольные прямые линии и ось бруса искривятся;

· Сечения бруса расширятся в поперечном направлении на вогнутой стороне и сузятся на выпуклой стороне.

Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью.

При чистом изгибе волокна, лежащие на выпуклой стороне, растягиваются, а лежащие на вогнутой стороне – сжимаются, а на границе лежит нейтральный слой, волокна которого только искривляются, не изменяя своей длины. Поэтому при чистом изгибе в поперечном сечении бруса возникают только нормальные

напряжения, неравномерно распределенные по сечению, из-за искривления волокон и оси бруса.

Относительное удлинение при изгибе прямо пропорционально расстоянию до нейтральной оси .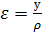

Для вычисления нормальных напряжений при изгибе используем закон Гука: 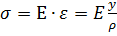. Эта зависимость определяет линейный закон распределения нормальных напряжений по сечению балки. По ширине балки напряжения постоянны. Наибольшего значения они достигают в точках сечения, наиболее удаленных от нейтральной оси. В точках нейтральной оси напряжения равны нулю.

Нормальные напряжения вычисляются по формуле: 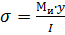, где I- осевой момент инерции. Для сечения разных форм есть формула.

Максимальное значение нормальные напряжения возникают с волокнах, наиболее удаленных от нейтральной оси: , где W- момент сопротивления изгибу.

Единица измерения .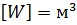

Определим моменты сопротивления изгибу наиболее распространенных сечений:

сечение	рисунок	формула
Прямоугольник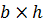
Прямоугольник
Круг диаметром d
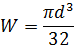
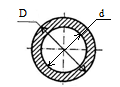
Кольцо

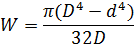
Дата добавления: 2014-12-25