КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Мощность при вращательном движении
|
|
|
|
Если вал машины передает скручивающий момент Мх, например, от мотора к станку, то значение момента зависит от передаваемой мощности и частоты вращения вала. Учитывая, что мощность равна работе в единицу времени 1Вт = 1Нм/с, можно составить равенство
 ,
,
где N – мощность, Вт (кВт);
Мх – момент, Н∙м;
ω – угловая скорость, 1/с:  .
.
Тогда скручивающий момент Мх определится по формуле
 ,
,
где n – число оборотов в минуту, об /мин.
Пример 9
Подобрать диаметр вала  (рис. 36), если даны диаметры шкивов
(рис. 36), если даны диаметры шкивов 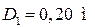 ,
, 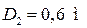 ; вес шкивов
; вес шкивов 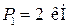 ,
,  ; натяжение ремней
; натяжение ремней  ,
,  ,
, 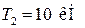 ,
,  ; длина вала
; длина вала 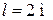 , угол наклона ремней второго шкива к оси Z
, угол наклона ремней второго шкива к оси Z  ; допускаемое напряжение материала вала равно
; допускаемое напряжение материала вала равно 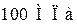 . Считать, что суммарный крутящий момент на шкивах полностью передается двигателю, подключенному в крайнем правом сечении вала.
. Считать, что суммарный крутящий момент на шкивах полностью передается двигателю, подключенному в крайнем правом сечении вала.
Решение. Вследствие действия сил натяжения и собственного веса шкивов вал будет подвержен деформации изгиба в вертикальной и горизонтальной плоскостях, а в результате разницы сил натяжения на каждом из шкивов появятся внешние скручивающие моменты, вызывающие кручение вала. Приводя силы натяжения ремней каждого шкива к центру сечения вала, находим внешние моменты 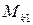 и
и  , вызывающие деформацию кручения:
, вызывающие деформацию кручения:
 ;
;
 .
.
Определив значение внешних моментов, найдем направления действия 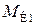 и
и  .
.
Так как внешние моменты определяются разницей сил натяжения на шкивах, то направления  определяются направлением большей силы натяжения. Так,
определяются направлением большей силы натяжения. Так, 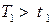 , и поэтому
, и поэтому 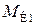 направлен по часовой стрелке (рис. 36). Составим расчетную схему при кручении (см. рис. 36, а). Построим эпюру крутящих моментов (см. рис. 36, б).
направлен по часовой стрелке (рис. 36). Составим расчетную схему при кручении (см. рис. 36, а). Построим эпюру крутящих моментов (см. рис. 36, б).
Теперь рассмотрим последовательно деформации изгиба в вертикальной и горизонтальной плоскостях. Для составления расчетных схем изгиба в этих двух плоскостях найдем проекции равнодействующих сил натяжения и веса шкивов на оси y и z. Снова определяем только значения этих проекций, а направление векторов сил учтем на расчетной схеме:
 ;
;
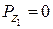 ;
;
 ;
;
 .
.
Составляем расчетную схему изгиба в вертикальной плоскости (см. рис. 36, в) и строим эпюру изгибающих моментов  (см. рис. 36, г.). Аналогично определяются изгибающие моменты
(см. рис. 36, г.). Аналогично определяются изгибающие моменты 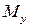 от сил, действующих в горизонтальной плоскости.
от сил, действующих в горизонтальной плоскости.
Найдем опасное сечение, где 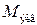 будет максимальным. В данном примере таким сечением будет сечение, где расположен второй шкив. В заданиях могут быть не такие очевидные случаи, поэтому надо сравнить значения
будет максимальным. В данном примере таким сечением будет сечение, где расположен второй шкив. В заданиях могут быть не такие очевидные случаи, поэтому надо сравнить значения 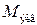 , как правило, в двух сечениях и выбрать наибольшее.
, как правило, в двух сечениях и выбрать наибольшее.
В данном примере 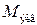 найдем по третьей теории прочности:
найдем по третьей теории прочности:
 .
.
Диаметр вала d при 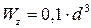 :
:
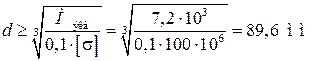 .
.
Принимаем диаметр вала  .
.

Рис. 36. Расчетные схемы и эпюры внутренних сил
при расчете вала на изгиб с кручением
Задача 10. Сложное сопротивление. Кручение и изгиб
Определить диаметр вала (рис. 37), если  . Считать, что суммарный крутящий момент на шкивах полностью передается двигателю, подключенному в крайнем правом сечении вала.
. Считать, что суммарный крутящий момент на шкивах полностью передается двигателю, подключенному в крайнем правом сечении вала.
План решения:
1) построить эпюру крутящих моментов 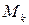 ;
;
2) построить эпюры изгибающих моментов 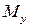 и
и  ;
;
3) определить эквивалентный момент 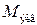 ;
;
4) подобрать диаметр вала d. Собственным весом шкивов пренебречь.
Данные к задаче приведены в табл. 11.
Таблица 11
Данные к задаче 10
| Номер строки | Номер схемы | l, м | 
| 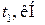
| 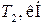
| 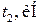
| 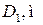
| 
| αo |
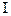 ,а ,а
| 1,0 | 0,2 | 0,5 | ||||||
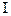 ,б ,б
| 1,2 | 0,3 | 0,6 | ||||||
 ,а ,а
| 1,4 | 0,4 | 0,7 | ||||||
 ,б ,б
| 1,6 | 0,5 | 0,8 | ||||||
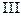 ,а ,а
| 1,8 | 0,6 | 0,9 | ||||||
 ,б ,б
| 2,0 | 0,7 | 1.0 | ||||||
 ,б ,б
| 2,2 | 0,5 | 0.9 | ||||||
 ,а ,а
| 2,4 | 0,5 | 0,8 | ||||||
 ,б ,б
| 2,6 | 0,4 | 0,7 | ||||||
 ,а ,а
| 2,8 | 0,3 | 0,6 | ||||||
| в | а | б | в | А | б | в | а | б |

Рис. 37. Схемы к задаче 10
Вопросы для самоконтроля
1. В каких точках сечения сочетание напряжений получается наиболее опасным для прочности вала?
2. Как находится опасное сечение вала, работающего на изгиб и кручение?
3. Как определяется скручивающий момент по мощности, передаваемой валом, и по числу оборотов в минуту?
Глава 9. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Под действием сжимающей силы стержень может утратить первоначальную форму равновесия и искривиться. Произойдет потеря устойчивости стержня. Наименьшая сила, при которой происходит потеря устойчивости, называется критической и определяется по формуле Эйлера:
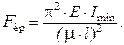
где Е – модуль упругости материала стержня;
I min – минимальный осевой момент инерции сечения стержня;
μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня (рис. 38);
l – длина стержня, μ ∙ l = l пр – приведенная длина стержня.
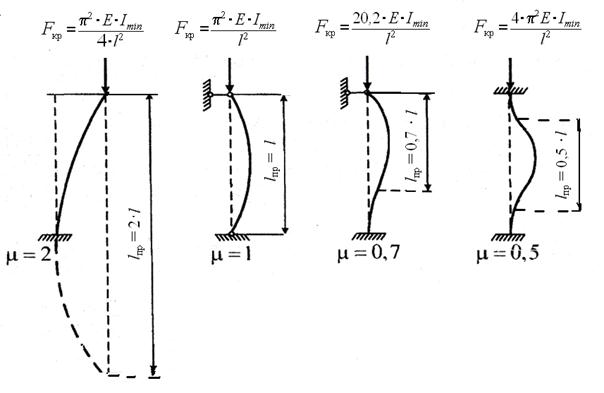
Рис. 38. Значения коэффициента μ приведенной длины и критической
силы F кр для сжатых стержней при различных способах закрепления концов
Напряжения, вызванные критической силой, называются критическими и определяются по формуле Эйлера:
 ,
,
где λ – гибкость стержня,  , (
, (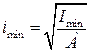 – минимальный радиус инерции сечения);
– минимальный радиус инерции сечения);
А – площадь поперечного сечения стержня.
Формула Эйлера применима при условии, что критическое напряжение не превышает предела пропорциональности материала  . Обычно это условие выражают через гибкость стержня и записывают в виде
. Обычно это условие выражают через гибкость стержня и записывают в виде

где 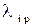 – предельное значение гибкости, которое определяет границу применимости формулы Эйлера.
– предельное значение гибкости, которое определяет границу применимости формулы Эйлера.
Формулой Эйлера можно пользоваться, если гибкость стержня 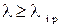 , если
, если  , то пользоваться формулой Эйлера нельзя.
, то пользоваться формулой Эйлера нельзя.
При значениях гибкости от 0 до 40  50 стержень настолько короткий, что практически разрушается при потере прочности, поэтому критическое напряжение равно пределу текучести:
50 стержень настолько короткий, что практически разрушается при потере прочности, поэтому критическое напряжение равно пределу текучести: 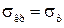 .
.
При значениях гибкости, лежащих в интервале 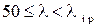 , стержень теряет устойчивость, деформируясь в упруго-пластической области, поэтому критическое напряжение
, стержень теряет устойчивость, деформируясь в упруго-пластической области, поэтому критическое напряжение  определяют по эмпирической формуле Ф. С. Ясинского:
определяют по эмпирической формуле Ф. С. Ясинского:
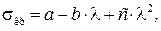
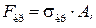
где а, b, с – коэффициенты, зависящие от материала и имеющие размерность напряжения. Они приведены в табл. 12.
Таблица 12
Опытные коэффициенты для определения  , МПа
, МПа
| Материал | а | b | с |
| Сталь Ст3 Сталь Ст5 Чугун Сосна (сжатие вдоль волокон) | 29,3 | 1,14 3,62 0,194 | 0,053 |
Критическая сила является недопустимой для сжатых стержней.
Определение допускаемой сжимающей силы [ F ] производят двумя способами. Первый способ используется, когда для рассчитываемого стержня известны длина, способ закрепления концов, форма и размеры поперечного сечения, материал, коэффициент запаса на устойчивость. Вначале определяют критическую силу F кр = sкр ∙ А, а затем допускаемую силу [ F ]:
 ,
,
где [ n у] – допускаемый коэффициент запаса на устойчивость.
Значения допускаемых коэффициентов запаса на устойчивость [ n у] для различных материалов приведены в табл. 13.
Таблица 13
Допускаемые коэффициенты запаса на устойчивость
для различных материалов
| Материал | [ n y] |
| Сталь Ст 3 | 1,8  3 3
|
| Сталь Ст 5 | 1,8  3 3
|
| Чугун | 5  5,5 5,5
|
| Сосна (сжатие вдоль волокон) | 2,8  3,2 3,2
|
Второй способ основан на применении таблиц j (l). Сначала определяют гибкость стержня λ, затем по таблице находят j (l) и вычисляют [ F ] по формуле
[ F ] = j . [sс] . А,
где j – коэффициент уменьшения допускаемого напряжения при сжатии [sс].
Значения коэффициента j в зависимости от гибкости λ и материала стержня приведены в табл. 14.
Для расчета критического напряжения, критической силы, допускаемой сжимающей силы и коэффициента запаса на устойчивость
можно использовать блок-схему, представленную на рис. 39.
Таблица 14
Значение коэффициента продольного изгиба j (l)
для различных материалов
| Гибкость λ | Значение j (l) | |||
| Сталь Ст3, Ст4 | Сталь Ст5 | Чугун | Дерево | |
| 1,00 | 1,00 | 1,00 | 1,00 | |
| 0,99 | 0,98 | 0,97 | 0,99 | |
| 0,97 | 0,96 | 0,91 | 0,97 | |
| 0,95 | 0,93 | 0,81 | 0,93 | |
| 0,92 | 0,89 | 0,69 | 0,87 | |
| 0,89 | 0,85 | 0,57 | 0,80 | |
| 0,86 | 0,80 | 0,44 | 0,71 | |
| 0,81 | 0,74 | 0,34 | 0,60 | |
| 0,75 | 0,67 | 0,26 | 0,48 | |
| 0,69 | 0,59 | 0,20 | 0,38 | |
| 0,60 | 0,50 | 0,16 | 0,31 | |
| 0,52 | 0,43 | – | 0,25 | |
| 0,45 | 0,37 | – | 0,22 | |
| 0,40 | 0,32 | – | 0,18 | |
| 0,36 | 0,28 | – | 0,16 | |
| 0,32 | 0,25 | – | 0,14 | |
| 0,29 | 0,23 | – | 0,12 | |
| 0,26 | 0,21 | – | 0,11 | |
| 0,23 | 0,19 | – | 0,10 | |
| 0,21 | 0,17 | – | 0,09 | |
| 0,19 | 0,15 | – | 0,08 | |
| 0,17 | 0,14 | – | – | |
| 0,16 | 0,13 | – | – |

Рис. 39. Блок-схема вычисления σкр, F кр, [ F ] и n у
Практически расчет на устойчивость ведется с использованием коэффициента j – коэффициента уменьшения допускаемого напряжения при сжатии [sс].
Условие устойчивости имеет вид

Расчет на устойчивость сводится к недопущению потери устойчивости, т.е. искривления стержня.
Подбор поперечного сечения стержня при заданных длине, сжимающей силе и материале выполняется с использованием таблиц значений j (l) методом последовательных приближений в следующем порядке.
1. Задают произвольное значение j. Например, полагают j = 0,5.
2. Вычисляют допускаемое напряжение на устойчивость:
[sу] = j ∙ [sс].
3. Определяют площадь поперечного сечения из условия
устойчивости:
A бр³ F / (j ∙ [sс]).
4. Подбирают размеры сечения или номер профиля. Вычисляют
площадь А, минимальный момент инерции I min, минимальный радиус инерции i min поперечного сечения.
5. Определяют гибкость стержня l.
6. Если гибкость стержня l > 220, то считают, что заданная сила
F равна допускаемой [ F ]:
 ,
,
где F кр – критическая сила (определяется по формуле Эйлера), а n у – коэффициент запаса на устойчивость (выбирается по табл. 13).
Тогда можно определить значение наименьшего момента инерции I min по формуле
 .
.
7. Если гибкость стержня l 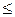 220, то для полученной гибкости
220, то для полученной гибкости
находят истинное значение jи.
8. Вычисляют действующее напряжение s =  .
.
9. Вычисляют допускаемое напряжение [sу] = jи ∙[sс].
10. Сравнивают действующее напряжение с допускаемым, вычисляя относительную разницу k: k =  .
.
11. Если k > 0, то имеем недонапряжение, если k < 0, то имеем
перенапряжение.
12. Сечение считают подобранным, если s и [sу] отличаются не
более, чем на 5%, т.е. |k| £ 5%.
13. Если |k| > 5%, то в качестве второго приближения берут
j2 = j + jи и повторяют расчет, пока не будет выполняться условие |k| £ 5%.
Подбор сечения по изложенному алгоритму представлен в виде
блок-схемы (рис. 40).
В сопротивлении стержней продольному изгибу основную роль
играет гибкость стержня и, следовательно, величина наименьшего радиуса инерции сечения, поэтому существенным является вопрос не только величины площади сечения, как при расчете на прочность, но и формы поперечного сечения.
Для наиболее оптимального выбора сечения необходимо
конструировать сечение так, чтобы при определенной площади
величина наименьшего радиуса инерции была бы возможно большей. Для этого прежде всего следует стремиться к тому, чтобы центральные моменты инерции сечения были равны. Такой стержень будет оказывать одинаковое сопротивление потере устойчивости в любом направлении.
Далее, необходимо стремиться к получению при данной площади
наибольших центральных моментов инерции. Для этого надо разместить материал сечения по возможности дальше от центра тяжести. Этим условиям хорошо удовлетворяют трубчатое сечение или сечение, составленное из двух швеллеров, раздвинутых на определенное расстояние.
На выбор материала для сжатых стержней влияют два фактора:
1. Если sкр < sпц (при большой гибкости), то единственной
механической характеристикой, влияющей на устойчивость, является модуль продольной упругости Е, а Е мало зависит от марки стали. Поэтому для тонких и длинных стержней применяют низколегированные стали.
2. Для стержней средней и особенно малой гибкости sкр
существенно зависит от предела текучести или предела прочности материала. Применение высоколегированных сталей для этих стержней дает существенную экономию материала.
Значение проверки на устойчивость велико. Достаточно сказать,
что все значительные катастрофы инженерных сооружений произошли вследствие потери устойчивости сжатых элементов конструкции. Особая опасность потери устойчивости заключается в том, что обычно она наступает внезапно.
|

Рис. 40. Блок-схема подбора сечения из расчета на устойчивость
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 3635; Нарушение авторских прав?; Мы поможем в написании вашей работы!