Пример 11. Определить величину и sкр для дюралюминиевого стержня кольцевого сечения: , ,

Пример 10

Определить величину 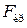и s_кр для дюралюминиевого стержня кольцевого сечения: 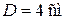, , 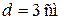, , 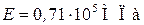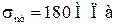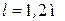(рис. 41).

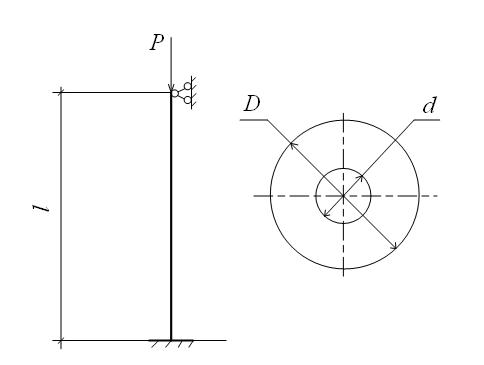
Рис 41. Определение критической силы для стержня

кольцевого сечения

Осевой момент инерции кольцевого сечения стержня:

.

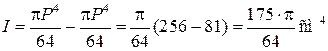Площадь поперечного сечения стержня:

.

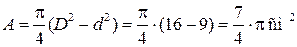Радиус инерции поперечного сечения:

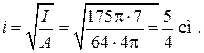
При заданном способе закрепления концов стержня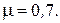

Гибкость стержня: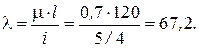

Критерий применимости формулы Эйлера:

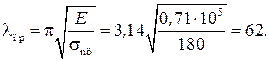
Так как 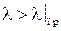, то 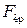можно определить по формуле Эйлера:

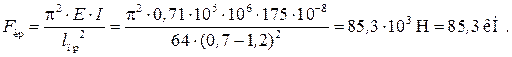
Критическое напряжение:

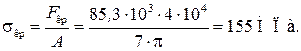
Колонна, составленная из двух швеллеров (рис. 42), нагружена силой

F = 200 кН, l = 2,5 м.

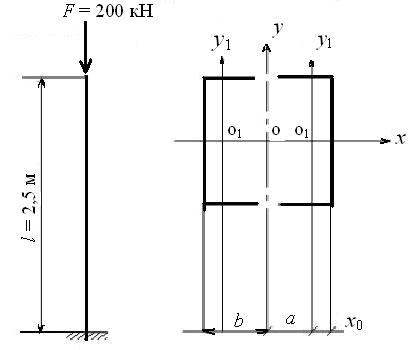
Рис. 42. Подбор поперечного сечения колонны

из расчета на устойчивость

Подобрать номер швеллера, если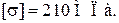

Сначала нужно выявить главную центральную ось заданного сечения из двух швеллеров с минимальным значением момента инерции. В нашем примере такой осью будет ось симметрии o y (см. рис. 42).

Момент инерции произвольного сечения относительно оси o y, параллельной главной оси сечения o y ₁ и удаленной от нее на расстояние a, можно вычислить по формуле

,

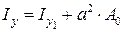где 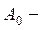площадь сечения.

Так как наша колонна состоит из двух одинаковых швеллеров, состыкованных вплотную друг к другу, то

,

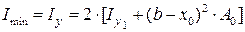где А ₀ – площадь одного швеллера.

Площадь всего сечения А = А ₀.

Подбор размеров сечения ведется путем последовательного приближения. Обычно задают значение φ и определяют A. Для первого приближения примем произвольно 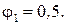Тогда из условия устойчивости

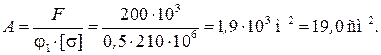
По сортаменту (ГОСТ 8240 – 72) исследуем швеллер № 10:

, , , .

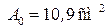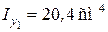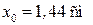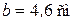Для рассматриваемого сечения, состоящего из двух швеллеров

№ 10, имеем:

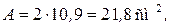
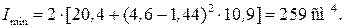
Гибкость колонны 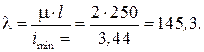Для стержня с защемленным концом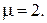

По таблице для стали марки Ст3, интерполируя, находим истинное значение 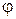для выбранного профиля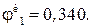

Действующее напряжение: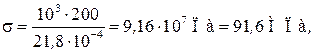

допустимое напряжение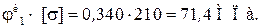

Перенапряжение составляет 28,4%.

Второе приближение.

Задаемся тогда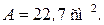

Исследуем швеллер № 12,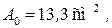

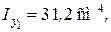
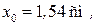
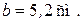
Для сечения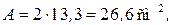

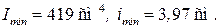
Гибкость колонны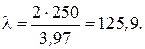

Коэффициент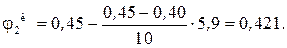

Напряжение в колонне:

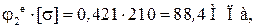
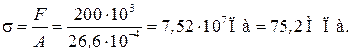
Недонапряжение составляет 15,1%.

Анализируя расчеты, заметим, что сечение из двух швеллеров

№ 10 дает большое перенапряжение, а из двух швеллеров № 12 – существенное недонапряжение. Уменьшить это недонапряжение мы не можем, так как ближайший стандартный профиль с меньшим поперечными размерами – это уже рассмотренный нами швеллер № 10.

Поскольку размеры сечений прокатных профилей от номера к номеру изменяются скачкообразно, во многих случаях не удается подобрать такое сечение, чтобы расхождение в напряжениях не превышало 5 %.

Итак, принимаем сечение из двух швеллеров № 12.

Задача 11. Устойчивость сжатых стержней

Выполнить расчет на устойчивость центрального сжатого стержня из стали марки Ст3, имеющего двутавровое сечение (рис. 43), если 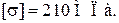Данные к задаче приведены в табл. 15.

План решения задачи:

1) при предварительно заданном значении 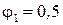определить размеры поперечного сечения (номер двутавра);

2) проверить устойчивость стержня при предварительно вычисленных размерах сечения;

3) если устойчивость стержня не обеспечивается или имеет место большое недонапряжение, произвести повторный расчет с новым значением:

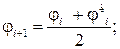
4) повторять п. 3, пока не будет найден оптимальный номер двутавра.

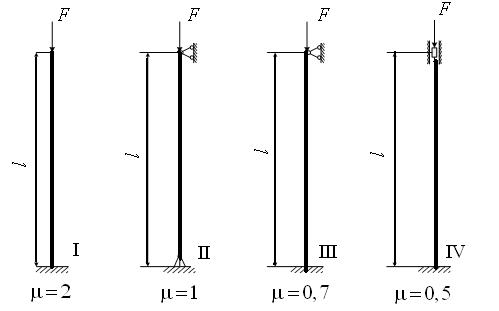
Рис. 43. Схемы к задаче 11

Таблица 15

Данные к задаче 11

Номер строки	Номер схемы	F, кН	l, м
	I		4,1
	II		4,2
	III		4,3
	IV		4,4
	I		4,5
	II		4,6
	III		4,7
	IV		4,8
	I		4,9
	II		5,0
	в	б	а

Вопросы для самоконтроля

1. Что называется критической силой?

2. Как определяется запас устойчивости?

3. Как учитывается влияние способа закрепления концов сжатого

бруса на величину критической силы?

4. Что называется коэффициентом длины и как он определяется?

5. Что называется гибкостью сжатого бруса и как она определяется?

6. На чем основывается установление границ применимости формулы Эйлера?

7. Два стержня шарнирно оперты по концам и сжаты силами F. Поперечное сечение одного из них круглое, а другого – квадратное. Для какого из стержней критическая сила окажется больше, если модуль упругости, длина и площадь поперечного сечения у них одинаковы?

Глава 10. ДИНАМИЧЕСКОЕ ДЕЙСТВИЕ НАГРУЗОК

Под действием нагрузки элементы конструкции деформируются и

перемещаются. Перемещения происходят с ускорением, отчего возникают силы инерции.

При статическом действии нагрузка изменяется медленно. Ускорения

перемещений элементов конструкций, а, следовательно, и силы инерции весьма малы и поэтому их можно не учитывать.

При динамическом действии нагрузка изменяется быстро,

воздействует резко. Перемещения элементов конструкции происходят с заметным ускорением. Возникающие силы инерции существенны и подлежат учету.

Усилия, напряжения и перемещения от динамического действия

нагрузки в K _д раз больше, чем от статического действия той же нагрузки:

,

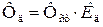где 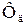– фактор от динамического действия нагрузки;

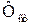– фактор от статического действия той же нагрузки;

K _д – коэффициент динамичности.

Для учета сил инерции при подъеме груза с ускорением

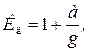
где a – ускорение, с которым движется груз;

g – ускорение свободного падения.

При ударном действии груза (без учета массы ударяемого элемента)

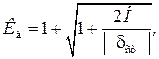
где H – высота падения груза;

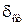– перемещение точки приложения груза от его статического действия.

При продольном ударе .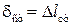

При поперечном (изгибающем) ударе .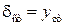

Пример 12

Груз весом 500 H падает с высоты 65 см на деревянную балку длиной 3 м и сечением 12 х 20 см (рис. 44). Проверить прочность балки, если 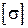=10 МПа и Е = 1 ГПа.

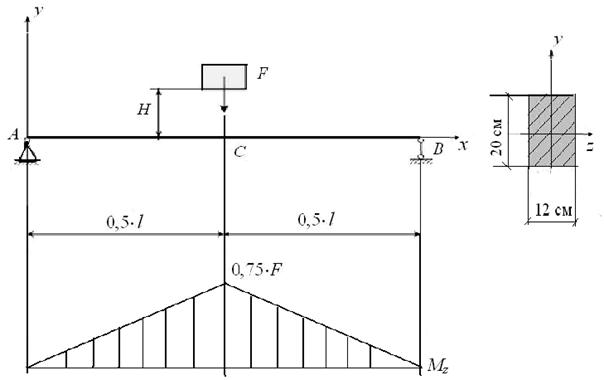
Рис. 44. Удар груза по балке

Балка подвергается поперечному (изгибающему) удару.

Условие прочности балки:

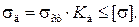
Напряжение в балке от статического действия груза:

.

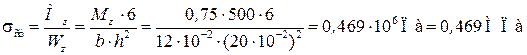Для определения коэффициента динамичности необходимо знать величину прогиба в точке приложения груза от его статического действия. Воспользуемся методом начальных параметров и составим уравнение прогибов:

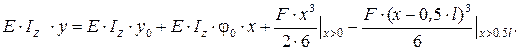
Так как начало отчета абсциссы х принято на опоре А, начальный

прогиб 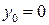. Определим :

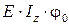При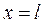

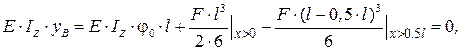
откуда .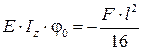

При .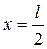

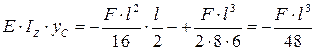Прогиб при 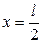в точке С равен

.

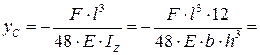
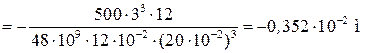Коэффициент динамичности:

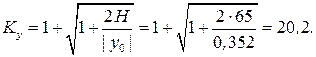
Динамическое напряжение:

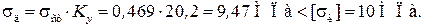
Прочность балки обеспечена.

Задача 12. Динамическое действие нагрузок

Произвести расчет балки при ударном действии груза весом 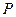(рис.45). Материал балки – сталь, 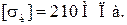Данные к задаче приведены в табл. 16.

Таблица 16

Данные к задаче 12

Номер строки	Номер схемы	Вес груза P, кН	Номер двутавра	Длина l, м	Высота падения H, м
	I	1,10		2,1
	II	1.20	22а	2,2
	III	0.30		2,3
	IV	0.40	24а	2,4
	V	0.50		2,5
	VI	0.60	27а	2,6
	VII	0.70		2,7
	VIII	0.80	30а	2,8
	IX	0.90		2,9
	X	1,00		3,0
	в	б	а	в	в

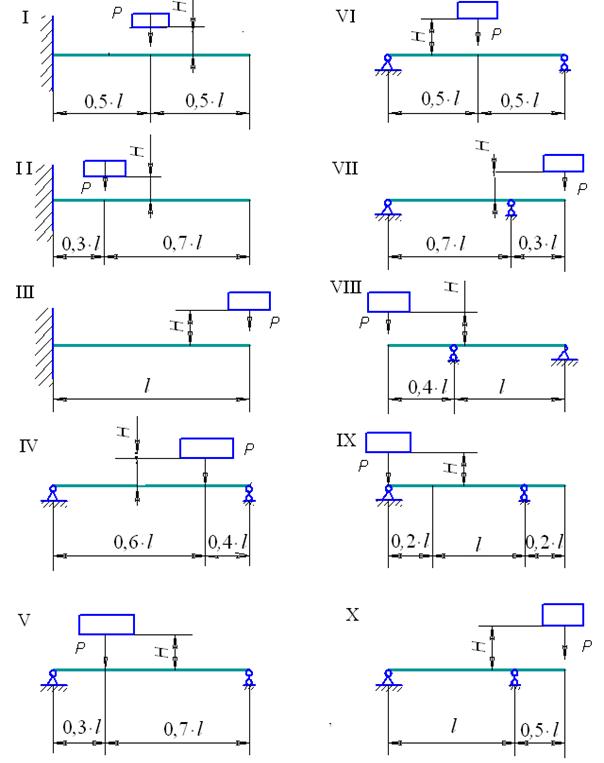
Рис. 45. Схемы балок к задаче 12

План решения задачи:

1) определить максимальное нормальное напряжение в балке при

статическом действии веса P;

2) определить прогиб балки в точке приложения веса P от

статического его действия;

3) вычислить динамический коэффициент;

4) вычислить максимальное нормальное напряжение от

динамического действия веса 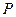и сделать заключение о прочности балки;

5) вычислить прогиб от динамического действия веса 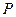в точке его приложения.

Примечание. Прогиб от статического действия груза весом P (в точке его приложения) определить по следующей формуле, взятой из справочника:

– в схемах I – III: ;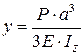

– в схемах IV – VI: ;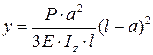

– в схемах VII – X: .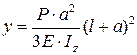

Вопросы для самоконтроля

1. Чем отличается динамическое нагружения от статического?

2. Что такое динамический коэффициент и чему он равен при подъеме груза с постоянным ускорением?

3. Что такое удар? Какие допущения используются при определении динамического коэффициента при ударе?

4. Запишите формулу для динамического коэффициента при ударе. Объясните влияние на него величины .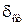

Заключение

В пособии изложены основные теоретические положения по простым и сложным видам деформации, напряженному и деформированному состоянию в точке, устойчивости сжатых стержней и динамическому действию нагрузок. Рассмотрены также такие темы курса «Сопротивление материалов», как «Метод расчета на прочность по допускаемым напряжениям», «Статически неопределимые системы при растяжении - сжатии и при изгибе», «Определение моментов инерции плоских сечений».

Приведены решения типовых задач по указанным разделам. В некоторых задачах представлены различные способы их решения. Составлены задания для выполнения контрольных работ. Разработана схема выбора индивидуального задания для студентов, в основу которой положен номер зачетной книжки студента.

Вопросы для самоконтроля позволяют студентам проверить усвоение изучаемого материала.

Дата добавления: 2014-12-26