Определение перемещений при плоском изгибе

Перемещения при плоском изгибе характеризуются прогибом y и углом поворота поперечного сечения φٕ, величины которых определяются из универсального уравнения изогнутой оси балки:

,

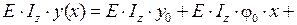
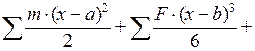
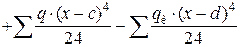где y ₀, φ₀ – прогиб и угол поворота сечения в начале координат;

a, b – расстояние от начала координат до сечения, в котором

приложен внешний силовой фактор (F и m или опорная реакция);

с – расстояние от начала координат до начала приложения

распределенной нагрузки;

d – расстояние от начала координат до конца приложения

распределенной нагрузки (начала приложения компенсирующей распределенной нагрузки q _к);

x – абсцисса рассматриваемого сечения.

При использовании универсального уравнения начало координат всегда выбирается на левом конце балки. Это уравнение получено путем интегрирования приближенного дифференциального уравнения упругой линии балки:

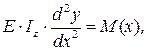
где 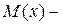изгибающий момент в сечении x.

Поэтому знаки у слагаемых, включающих F, m и q, будут определяться по правилу знаков для изгибающего момента при рассмотрении равновесия левой части балкой. По этой же причине в уравнения включаются только те силовые факторы, которые находятся слева от сечения с координатой x. Если распределенная нагрузка q не действует до правого конца балки, ее действие надо продолжить до этого конца и, соответственно, приложить равнозначную компенсирующую нагрузку q _к, которая учитывается в уравнении с противоположным основной q знаком. На эту особенность надо обратить внимание, так как при построении эпюр Q и M такой необходимости не возникало. Начальные параметры y ₀ и φ₀ определяются из условия, что на опорах прогибы равны нулю (см. далее прим. 7).

Для проверки правильности построения упругой линии балки можно использовать соответствие знака кривизны упругой линии и знака 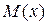. Если 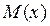>0, то на этом участке выпуклость упругой линии будет направлена вниз, и наоборот.

Пример 7

Определить прогибы в характерных сечениях балки (рис. 30) и построить ее изогнутую ось.

Построение эпюр Q и M, а также подбор сечения балки проделайте самостоятельно. Принимается двутавр № 16, , .

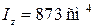Начало координат выбираем в крайнем левом сечении балки (на опоре С). Балка имеет три участка нагружения: I, II, III (см. рис. 30). Распределенная нагрузка q действует только на участке II. Доводим распределенную нагрузку q до конца балки и на этом участке III показываем компенсирующую (уравновешивающую) нагрузку.

Составим уравнение прогибов:

.

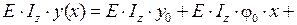
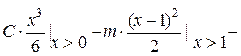
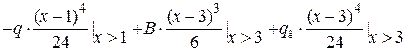Рассматриваемая балка имеет три участка нагружения. В уравнении прогибов отмечены участки, на которых учитывается каждый из силовых факторов. Слагаемые уравнения от соответствующего внешнего фактора имеют такой же знак, как и при определении изгибающего момента.

Начальные параметры y ₀ и φ₀ определим из условий, что на опорах балки прогибы равны нулю.

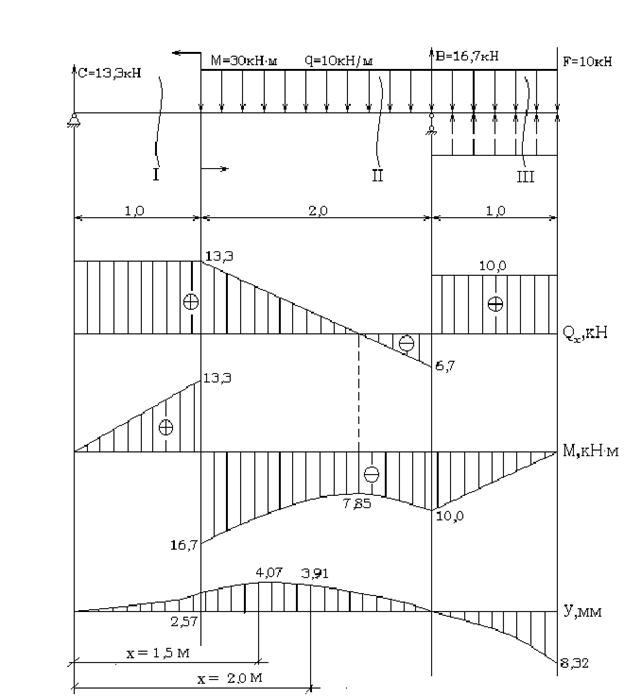
Рис. 30. Определение перемещений для двухопорной балки

При x = 0 .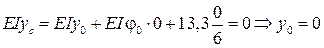

При x = 3 м ,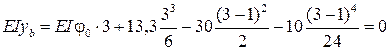

откуд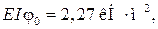а а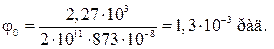

Положительное значение откладывается против хода часовой стрелки.

Определим прогибы в некоторых сечениях балки.

При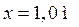

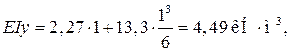
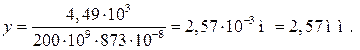
Величину прогиба при 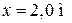определите самостоятельно (получится ).

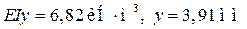В межопорной части балки максимальный прогиб будет примерно посередине пролета.

При х = 1,5 м ,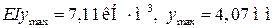

При х =4,0 м

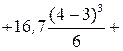
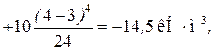
В некоторых случаях начало координат может быть выбрано на свободном конце балки. В этом случае 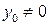и 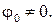Если начало координат в опорном защемлении, то 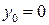и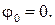

Задача 8. Определение перемещений при плоском изгибе

Определить перемещение балки и изобразить вид упругой линии балки, если Е = 2∙10¹¹ Па, 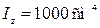(рис. 31).

План решения задачи:

1) определить опорные реакции;

2) построить эпюру ;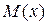

3) вычислить величины прогибов в характерных сечениях;

4) изобразить вид упругой линии балки.

Данные к задаче 8 приведены в табл. 9.

Таблица 9

Данные к задаче 8

Номер строки	Номер схемы	Нагрузки	Длина a, м
F, кН	М, кН∙м	q, кН/м
	I				1,0
	II				1,2
	III				1,4
	IV				1,6
	V				1,8
	VI				2,0
	VII				1,9
	VIII				1,7
	IX				1,5
	X				1,3
	в	а	б	в	б

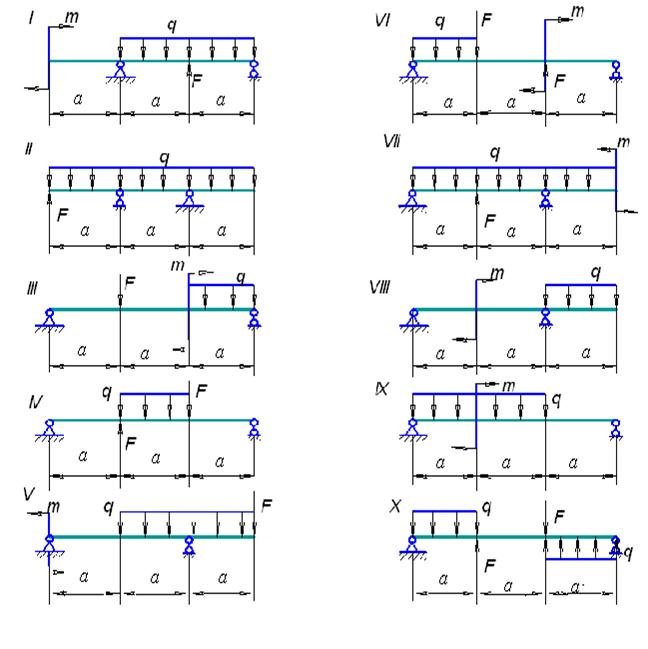
Рис. 31. Схемы балок к задаче 8

Вопросы для самоконтроля

1. Какие типы опор применяются для соединения балок с основанием и какие реактивные усилия могут возникать в этих опорах?

2. Какие уравнения равновесия применяются для определения опорных реакций и как проверить правильность определения опорных реакций?

3. При какой нагрузке на брус получается явление, называемое чистым изгибом?

4. Какой изгиб называется поперечным и какие внутренние усилия возникают в поперечных сечениях балки при поперечном изгибе?

5. Какое правило знаков принято для поперечной силы и изгибающего момента?

6. Когда изгиб балки называется плоским?

7. Какие зависимости существуют между поперечной силой, изгибающим моментом и интенсивностью вертикальной распределенной нагрузки?

8. Какие следствия вытекают из дифференциальных зависимостей при поперечном изгибе и как они используются при построении эпюр поперечных сил и изгибающих моментов?

9. Какая геометрическая характеристика сечения определяет прочность по нормальным напряжениям при изгибе?

10. Как распределяются нормальные напряжения по сечению балки?

11. Как определяется изгибающий момент и поперечная сила, передающиеся на отдельные элементарные объемы балки?

12. Как рассчитываются балки на прочность?

13. Как находится опасная точка в сечении при плоском изгибе?

14. В чем состоит общая идея метода начальных параметров? Запишите универсальную формулу для прогибов и углов поворота.

Глава 7. РАСЧЕТ НА ПРОЧНОСТЬ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ БАЛКИ

О принципе расчета статически неопределимых систем уже было сказано ранее (см. п.1.2). Рассмотрим на примере, как это делается применительно к балкам.

Пример 8

Определить размеры h, b прямоугольного поперечного сечения стальной балки (рис. 32, а), если [σ_и] = 160 МПа, E = 2·10⁵ МПа и h/b = 2. Определить прогибы посредине пролета балки и на конце консоли.

Число неизвестных реакций 4, уравнений статики 3: балка один раз статически неопределима. Целесообразные уравнения статики:

;

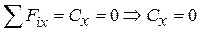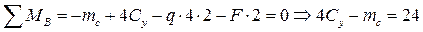. (13)

Дополнительное уравнение составим, исходя из условия, что на опоре B прогиб равен нулю:

.

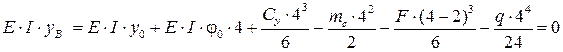Так как начало координат помещено в защемлении, начальные параметры y ₀ = 0 и φ₀ = 0. Тогда из уравнения прогибов получим:

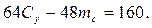(14)

Из уравнений (13) и (14) следует: 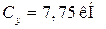, m_c = 7 кН∙м.

Определим опорную реакцию B:

,

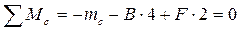откуда .

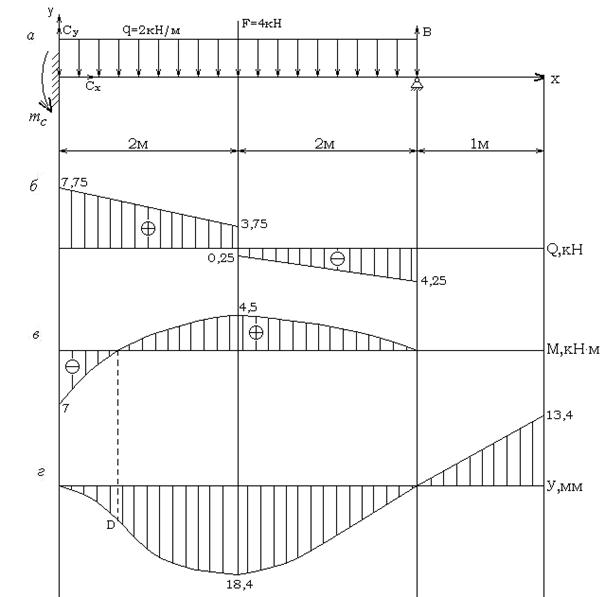
Рис. 32. Эпюры поперечных сил Q,

изгибающих моментов M и прогибов y

Проверка вычислений реакций:

.

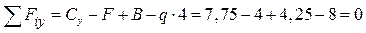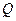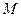Эпюры и показаны на рис. 32, б, в.

Размеры сечения балки определим из условия прочности по нор-мальным напряжениям:

; ;

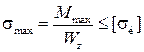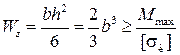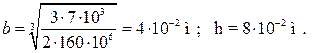
Момент инерции сечения

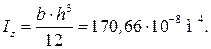
Жесткость сечения

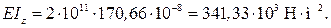
Прогиб посередине пролета балки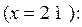

;

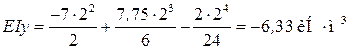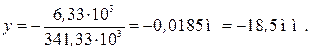
Прогиб на конце консоли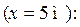

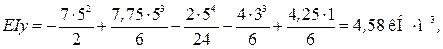
откуда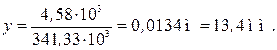

Изогнутая ось балки показана на рис. 32, г. Необходимо отметить,

что консольная часть балки не деформируется 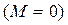, но перемещается за счет деформации пролетной части. Точка D – точка перегиба упругой линии.

Задача 9. Расчет статически неопределимой балки

Произвести расчет статически неопределимой балки (рис. 33).

Материал балки – сталь 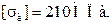Данные к задаче приведены

в табл.10.

План решения задачи:

1) раскрыть статическую неопределимость;

2) построить эпюры Q и M;

3) определить номер профиля сечения;

4) изобразить изогнутую ось балки, определив величины погибов в

характерных сечениях (не менее двух).

Примечание. Для раскрытия статической неопределимости следует

составить уравнения прогибов для шарнирной опоры и уравнение моментов относительно той же опоры.

Таблица 10

Данные к задаче 9

Номерстроки	Номерсхемы	Нагрузки	Длины участков, м
F, кН	М, кН·м	q, кН/м	а	в	с
	I				3,1	2,1	1,1
	II				3,2	2,2	1,2
	III				3,3	2,3	1,3
	IV				3,4	2,4	1,4
	V				3,5	2,5	1,5
	VI				3,6	2,6	1,6
	VII				3,7	2,7	1,7
	VIII				3,8	2,8	1,8
	IX				3,9	2,9	1, 9
	X				3,0	2,0	1,0
	в	а	б	в	а	б	в

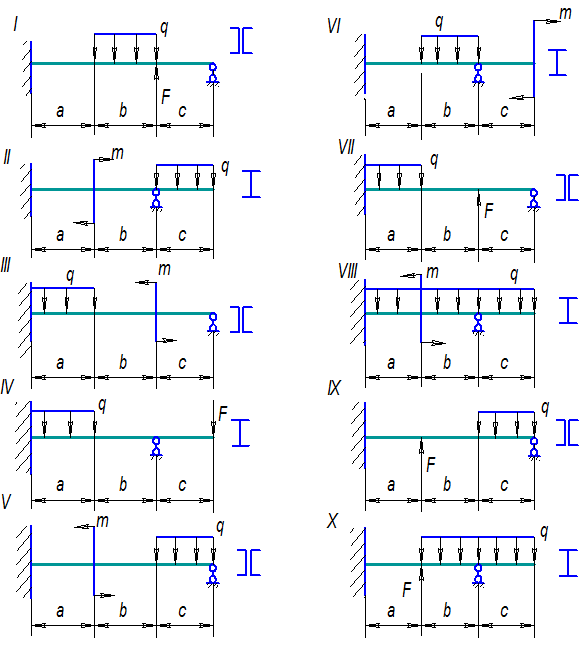
Рис. 33. Cхемы балок к задаче 9

Вопросы для самоконтроля

1. Какие системы называются статически неопределимыми и чем они отличаются от статически определимых систем?

2. Что такое основная система метода сил?

3. В чем заключается выбор основной системы?

4. Каков физический смысл уравнений деформаций?

Глава 8. СЛОЖНОЕ СОПРОТИВЛЕНИЕ.

Дата добавления: 2014-12-26