Состояние в точке

Для исследования напряженного состояния в точке деформируемого тела в ее окрестности выделяют элементарный объем в виде прямо­угольного параллелепипеда (рис. 8).

В общем случае деформирования напряженное состояние в точке характеризуется девятью величинами: тремя нормальными напряжениями σ _x, σ _y и σ _z и шестью касательными напряжениями – τ _xy, τ _xz, τ _yz, τ _zx, τ _yx, τ _zy.

Вследствие закона парности касатель­ных напряжений (τ _yz = τ _zy, τ _zx = = τ _xz, τ _xy = τ _yx) число независимых компонентов уменьшается до шести.

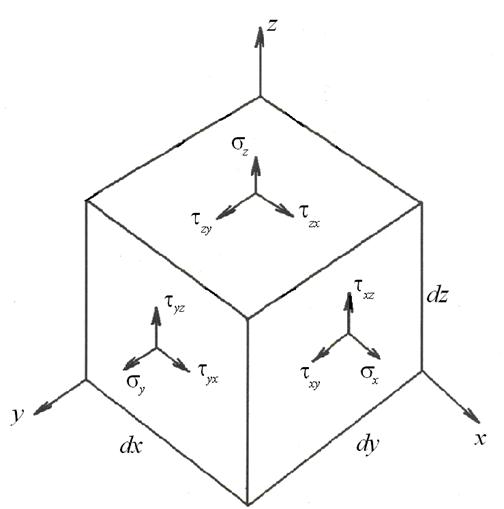
Рис. 8. Объемное напряженное состояние

Исследование напряженного состояния включает определение напряжений по произвольной площадке, проходящей через данную точку, а также положение главных площадок и значений главных нормальных напряжений. Среди бесконечно большого числа площадок, проходящих через данную точку тела, всегда найдутся по крайней мере три взаимно перпендикулярные площадки, на которых касательные напряжения отсутствуют. Такие площадки носят название главных площадок, а нормальные напряжения на них – главных норма­льных напряжений. Напряженное состояние в любой точке можно свести к растяжению или сжатию по одному, двум или трем взаимно перпендикулярным направлениям. В зависимости от этого различают линейное, пло­ское и объемное напряженное состояние (рис. 9).

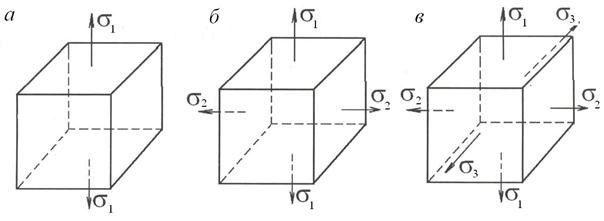
Рис. 9. Виды напряженного состояния:

а – линейное; б – плоское; в – объемное

Очень важно уметь определять значения главных нормальных напряжений в случае плоского напряженного состояния, которое наиболее часто встречается в брусе, подвергающемся действию изгибающих, скручивающих и растягивающих нагрузок, а также в тонкостенных оболочках.

Пример 3

Исследовать плоское напряженное состояние стального кубика

(рис. 10, а).

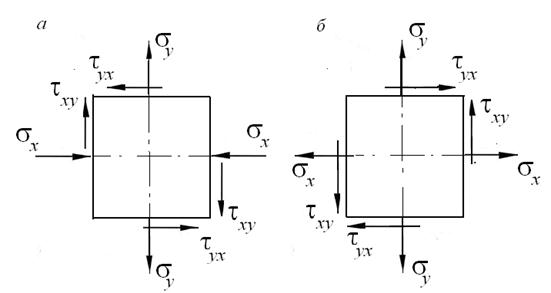
Рис. 10. Hормальные и касательные напряжения по граням кубика:

а – направления напряжений для исследуемого напряженного состояния;

б – положительные направления напряжений

Абсолютные величины напряжений (см. рис. 10, а):

σ _x = 100 МПа; σ _y = 70 МПа; τ _xy = τ _yx = 50 МПа; Е = 2 ·10⁵ МПа; μ = 0,25.

Прежде всего установим знаки нормальных и касательных напряжений, показанных на рис. 10, а. Положительные направления

нормальных напряжений σ _x, σ _y и касательных напряжений τ _xy = τ _yx показаны на рис. 10, б. Нормальные растягивающие напряжения принято брать со знаком плюс, а сжимающие – со знаком минус. Следовательно, σ _x = –100 МПа и σ _y = 70 МПа, τ _xy = –50 МПа.

Определение главных напряжений. Наибольшее σ₁:

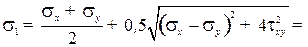
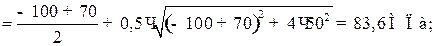
наименьшее из главных напряжений σ₂ :

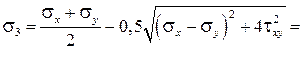
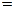
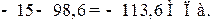
Определение направления главных площадок. Угол наклона нормали главной площадки к оси X определяется по формуле

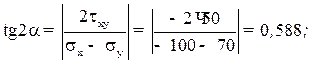
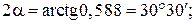
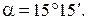
Знак касательных напряжений и угла α можно неустанавливать, если пользоваться следующим правилом для определения ориентации главных площадок.

Главные площадки, на которых действует наибольшее из главных напряжений σ_1, получаются поворотом на угол α тех из исходных площадок, на которых действует большее (по алгебраической величине) из исходных напряжений σ _x, σ _y. В нашем примере такими исходными площадками будут площадки, где действует нормальное напряжение σ _y, так как σ _y > σ _x.

Направление поворота указывает стрелка касательного напряжения на исходной площадке (рис. 11). Вторая пара главных площадок перпендикулярна найденным.

Определение максимальных касательных напряжений:

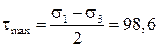МПа.

Эти напряжения действуют на площадках, наклоненных под углом 45° к главным, и направлены в сторону σ₁ (см. рис. 11).

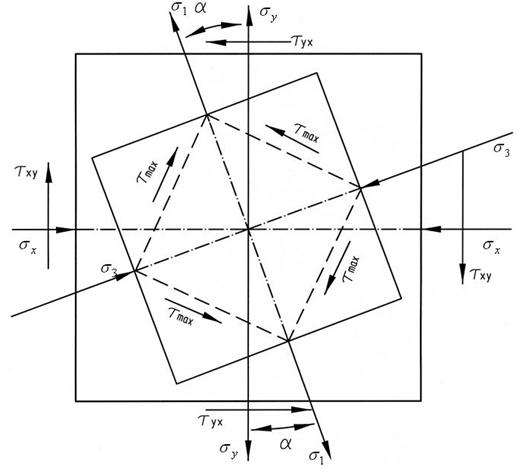
Рис. 11. Расположение главных площадок

Определение относительных деформаций ε _x, ε _y, ε _z:

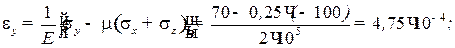
Обратите внимание на то, что при σ _z = 0 ε _z ≠ 0, т.е. при от­сутствии напряжения по оси Z деформация в этом направлении имеет место.

Определение относительного изменения объема θ:

.

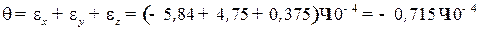Определение удельной потенциальной энергии деформаций. Потен- циальная энергия изменения объема U _об:

U _об 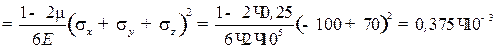МПа.

Потенциальная энергия изменения формы U _ф:

U _ф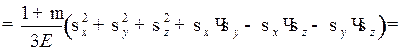

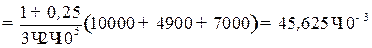МПа (Н/мм²).

Полная энергия U:

U = U _об + U _ф = 46·10^–3 = 46·10^–3 МПа (Н/мм²).

Задача 3. Плоское напряженное состояние

Исследовать плоское напряженное состояние (рис. 12). Данные к задаче приведены в табл. 3.

План решения задачи:

1) найти главные напряжения и направления главных площадок;

2) вычислить максимальные касательные напряжения;

3) определить относительные деформации;

4) найти относительное изменение объема;

5) найти удельную потенциальную энергию деформаций.

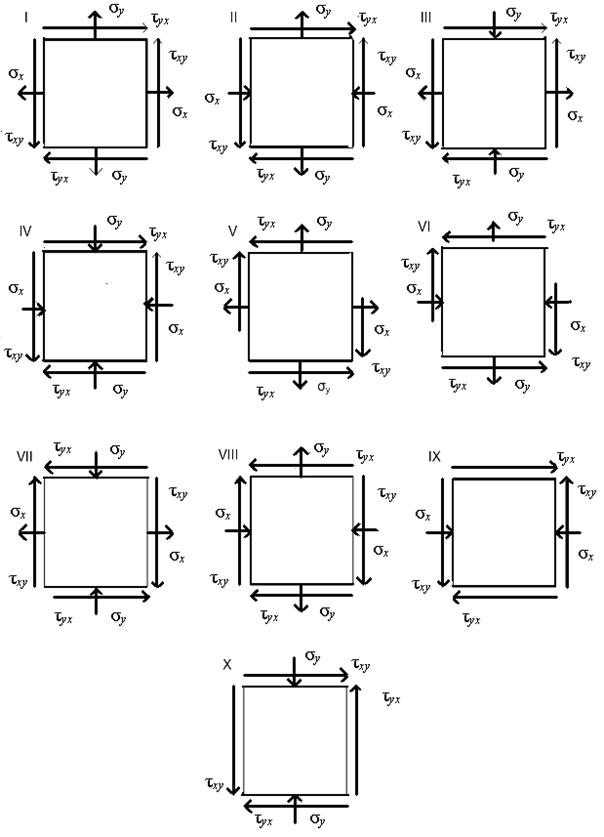
Рис. 12. Схемы к задаче 3

Таблица 3

Данные к задаче 3

Номер строки	Номер схемы	σ х, МПа	σ y, МПа	τ xy, МПа
	I
	II
	III
	IV
	V
	VI
	VII
	VIII
	IX
	X
	в	а	б	в

Вопросы для самоконтроля

1. Что такое напряженное состояние в точке?

2. Дайте понятие главных напряжений и трех основных видов напряженного состояния.

3. Чему равны касательные напряжения в главных площадках?

4. Как устанавливаются величины главных напряжений и положение главных площадок для плоского напряженного состояния?

5. Как расположены площадки с напряжениями τ_max и как они выражаются через главные напряжения?

6. Как связаны относительные линейные и объемная деформации в точке?

7. Напишите выражения удельной потенциальной энергии деформации в общем случае напряженного состояния в точке.

8. Что называется коэффициентом поперечной линейной деформации?

9. Как определяется линейная деформация при трехосной нагрузке?

10. Как формулируется закон парности касательных напряжений?

Глава 4. КРУЧЕНИЕ

При кручении в поперечном сечении стержня возникает крутящий момент М _К. Нагрузкой при кручении являются скручивающие моменты m_i, действующие относительно продольной оси стержня. Крутящий момент определяется методом сечений и равен алгебраической сумме внешних (скручивающих) моментов, действующих на рассматриваемую часть стержня: М _К = ∑ m_i. Момент считается положительным, если он направлен против хода часовой стрелки (при взгляде со стороны сечения).

При кручении в поперечном сечении стержня возникают касательные напряжения τ. Касательные напряжения τ распределяются по площади круглого поперечного сечения стержня неравномерно, нарастая от оси вала к поверхности по линейному закону, наибольшие напряжения возникают по контуру сечения. Закон распределения напряжений τ вдоль произвольного радиуса в сечении изображен на рис. 13. Во всех точках окружности радиуса ρ напряжение τ = const и направлено по касательной к этой окружности. Напряжения τ в сечении сводятся к крутящему моменту М _К (рис.13):

М _К = .

Формула для определения τ имеет вид

,

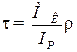где I_p – полярный момент инерции сечения, м⁴; для сплошного круглого сечения 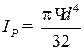(прил. 4);

М _К – крутящий момент, Н·м.

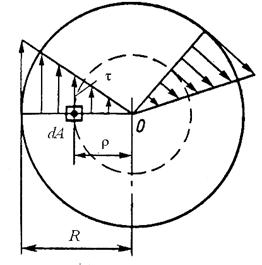
Рис. 13. Распределение касательных напряжений

в сечении при кручении

Условие прочности имеет следующий вид:

,

где 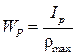– геометрическая характеристика прочности при кручении, называемая полярным моментом сопротивления, м³;

[τ_к] – допускаемое напряжение на кручение, Па.

Для сплошного круглого сечения (рис. 14)

.

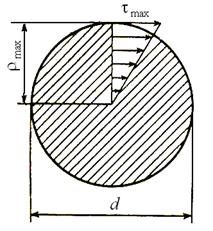
Рис.14. К определению полярного момента сопротивления W_p

для сплошного круглого сечения

Для полого толстостенного цилиндра (рис. 15)

.

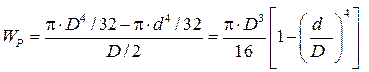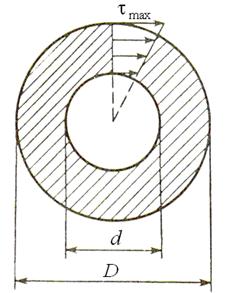
Рис. 15. К определению полярного момента сопротивления W_p

для полого толстостенного цилиндра

Деформация при кручении характеризуется углом закручивания на единицу длины стержня θ:

.

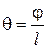Величина θ называется относительным углом закручивания и имеет размерность рад/м.

Условие жесткости имеет вид

,

где G – модуль упругости материала при сдвиге, Па.

Зависимость между модулями упругости Е и G имеет вид

,

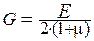где μ – коэффициент Пуассона;

[θ] – допускаемый относительный угол закручивания на единицу длины стержня (рад/м).

Диаметр стержня, работающего на кручение, определяется из двух условий: прочности и жесткости. Во внимание берется наибольший диаметр. Окончательное значение его принимается согласно стандарту.

Пример 4

Определить диаметры поперечных сечений участков стержня (вала) (рис. 16, а), если [τ_K] = 100 МПа, G = 80 ГПа, [θ] = 1,5^о/м. Построить эпюру углов поворота сечений φ.

[θ] = 1,5^о/м = 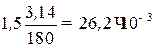рад/м.

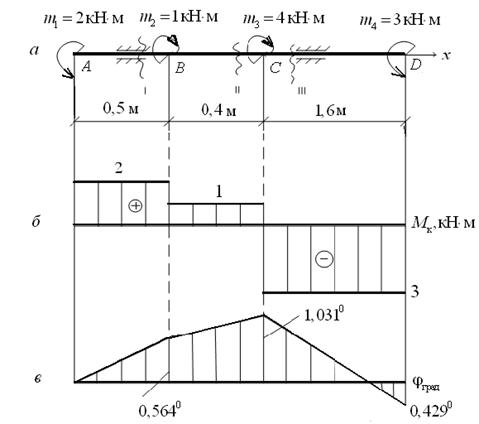
Рис.16. Построение эпюр крутящих моментов М _к

и углов поворота сечений φ:

а – расчетная схема; б – эпюра крутящих моментов М _к;

в – эпюра углов поворота сечений φ

Должно выполняться условие равновесия ∑ m_x = 0:

∑ m_x = m ₁ – m ₂ – m ₃ + m ₄ = 2 – 1 – 4 + 3 = 0.

Для определения крутящих моментов М _к на участках стержня будем рассматривать левую часть его.

Участок I: М _KI = m ₁ = 2 кН·м.

Участок II: М _KII = m ₁ – m ₂ = 2 – 1 = 1 кН·м.

Значение М _КIII определите самостоятельно (М _КIII = – 3 кН·м).

По вычисленным значениям М _к строится эпюра (см. рис. 16, б).

Преобразуем условия прочности и жесткости к виду, удобному для определения диаметра стержня.

Условие прочности:

, .

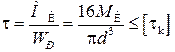Условие жесткости:

,

откуда

.

Вычисляем диаметр вала из условий прочности и жесткости.

На первом участке:

– диаметр вала из условия прочности

;

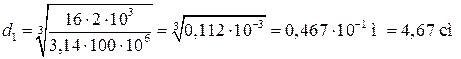– диаметр вала из условия жесткости

.

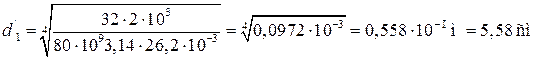Принимаем d ₁ = 6 см.

На втором участке:

– диаметр вала из условия прочности

;

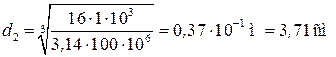– диаметр вала из условия жесткости

.

Принимаем d ₂ = 5 см.

Диаметр поперечного сечения на участке III рассчитайте самостоятельно (d ₃ = 5,35 см, d^’ ₃ = 6,18 см, принимаем d ₃ = 7 см).

Если стержень имеет постоянное сечение, то диаметр его определяется исходя из максимального значения М _к.

Определим деформации участков стержня:

.

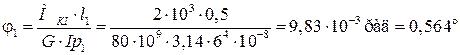Значения φ на других участках следующие:

.

Углы поворота характерных сечений (границ участков) равны:

;

.

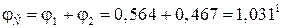Значение φ _D определите самостоятельно (φ _D = – 0,429^о).

Эпюра углов поворота сечений показана на рис. 16, в.

Вычислим максимальные напряжения на участках стержня:

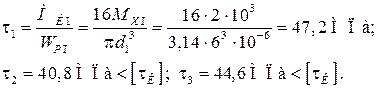
Вычисленные значения диаметров участков стержня обеспечивают его прочность и жесткость.

Задача 4. Кручение стержней с круглым сечением

Произвести расчет стального вала (рис. 17). Данные к задаче приведены в табл. 4.

План решения задачи:

1) построить эпюры крутящих моментов;

2) определить диаметр вала из расчета на прочность и округлить его до нормального размера (считать [τ _К ]=100 МПа);

3) определить диаметр вала из расчета на допускаемый угол

закручивания (принять [θ]=2⁰ на один погонный метр);

4) построить эпюру углов закручивания.

Таблица 4

Данные к задаче 4

Номер строки	Номер схемы	Расстояние, м	Момент, кН∙м
а	в	с	М 1	М 2	М 3
	I	1,1	1,1	1,1	1,1	1,1	1,1
	II	1,2	1,2	1,2	1,2	1,2	1,2
	III	1,3	1,3	1,3	1,3	1,3	1,3
	IV	1,4	1,4	1,4	1,4	1,4	1,4
	V	1,5	1,5	1,5	1,5	1,5	1,5
	VI	1,6	1,6	1,6	1,6	0,6	1,6
	VII	1,7	1,7	1,7	1,7	0,7	1,7
	VIII	1,8	1,8	1,8	1,8	0,8	1,8
	IX	1,9	1,9	1,9	1,9	0,9	1,9
	X	2,0	2,0	2,0	2,0	1,0	2,0
	в	а	б	в	а	б	в

Рис. 17. Схемы к задаче 4

Вопросы для самоконтроля

1. При какой нагрузке на брус получается деформация, называемая кручением?

2. Какая зависимость существует между модулями упругости G и Е?

3. Что называется крутящим моментом?

4. Как распределяются касательные напряжения по площади круглого сечения при кручении?

5. Как выражаются касательные напряжения при кручении через величину крутящего момента?

6. Как определяются относительный и абсолютный углы закручивания вала?

7. Какая существует дифференциально-интегральная зависимость между τ, М _к, φ, θ?

8. В чем состоит расчет на прочность и жесткость валов?

9. Что такое момент сопротивления сечения при кручении? В чем состоит условие прочности?

10. Как найти диаметр сечения вала, удовлетворяющего условиям прочности и жесткости?

11. Как формулируется закон Гука при сдвиге?

Глава 5. МОМЕНТЫ ИНЕРЦИИ ПЛОСКИХ СЕЧЕНИЙ

Любое плоское сечение характеризуется рядом геометрических характеристик: площадью, координатами центра тяжести, статическим моментом, моментом инерции и др.

Статические моменты относительно осей х и y равны:

, .

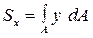Статические моменты обычно выражаются в кубических сантиметрах или метрах и могут иметь как положительные, так и отрицательные значения. Ось, относительно которой статический момент равен нулю, называется центральной. Точка пересечения центральных осей называется центром тяжести сечения. Формулы для определения координат центра тяжести x_c и y_c сложного сечения, разбитого на простейшие составные части, для которых известны площади А_i и положение центра тяжести x_ci и y_ci, имеют вид

, .

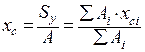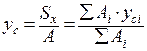Величина момента инерции характеризует сопротивляемость стержня деформации (кручения, изгиба) в зависимости от размеров и формы поперечного сечения. Различают моменты инерции:

– осевые, определяемые интегралами вида

, ;

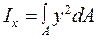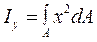– полярный:

;

– центробежный:

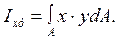
Осевые и полярные моменты инерции всегда положительны и не

обращаются в нуль. Полярный момент инерции I_p равен сумме осевых моментов инерции I_х и I_у относительно любой пары взаимно перпендикулярных осей х и у:

I_х + I_у = I_p = const.

Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Размерность моментов инерции — см⁴ или м⁴. Формулы для определения моментов инерции простых сечений относительно центральных осей приведены в справочниках. При вычислении моментов инерции сложных сечений часто используют формулы перехода от центральных осей простых сечений к другим осям, параллельным центральным.

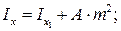
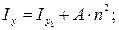
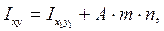
где 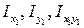– моменты инерции простых сечений относительно центральных осей;

m, n – расстояния между осями (рис. 18).

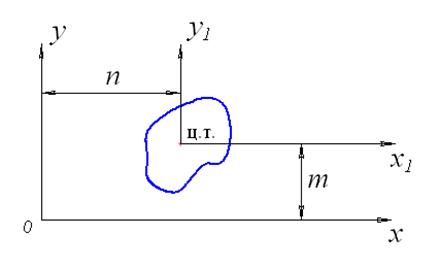
Рис. 18. К определению моментов инерции относительно осей,

параллельных центральным

Важное значение имеют главные центральные оси сечения. Главными центральными называются две взаимно перпендикулярные оси, проходящие через центр тяжести сечения, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции имеют экстремальные значения. Главные моменты инерции обозначаются I_{u (max)} и I_{v (min)} и определяются по формуле

.

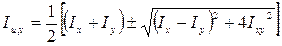Положение главных осей определяется углом α₀, который находится из формулы

.

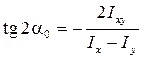Угол α₀ откладывается от оси с большим неглавным моментом инерции; положительное значение – против часовой стрелки.

Если сечение имеет ось симметрии, то эта ось является главной. Другая главная ось перпендикулярна оси симметрии. На практике часто используются сечения, составленные из нескольких прокатных профилей (двутавр, швеллер, уголок). Геометрические характеристики этих профилей приведены в таблицах сортамента. Для неравнобокого и равнобокого уголков центробежный момент инерции относительно центральных осей, параллельных полкам, определяется по формуле

.

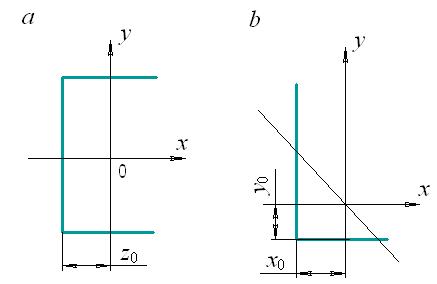
Обратите внимание на обозначение главных центральных осей в таблице сортамента для уголков. Знак I_xy для уголка зависит от положения его в сечении. На рис.19 показаны возможные положения уголка в сечении и приведены знаки для I_xy.

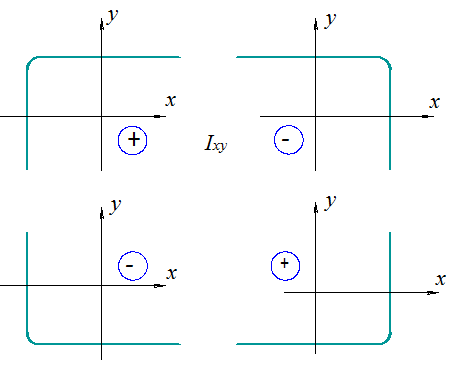
Рис. 19. Возможные положения уголка в сечении

и знаки для I_xy

Пример 5

Определить I_u, I_v и положение главных центральных осей сечения

(рис. 20).

Сложное сечение состоит из двух прокатных профилей. Выписка из таблиц сортамента (прил. 5) приведена на рис. 21.

В качестве вспомогательных примем оси, проходящие по внешним

сторонам швеллера (оси x_B, y_B, см. рис. 20).Координаты центра тяжести сечения:

;

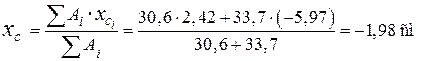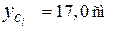(вычислите самостоятельно).

Рис. 20. Положение главных центральных осей инерции

U и V сложного сечения

В качестве вспомогательных можно было бы выбрать, например, центральные оси швеллера. Тогда несколько сократится объем вычислений.

Осевые моменты инерции:

.

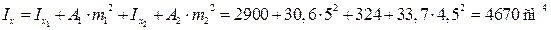Обратите внимание, что неравнобокий уголок в сечении расположен

иначе, чем показано в таблице сортаментов. Значение 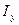вычислите самостоятельно .

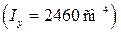№ 24 180 x 110 x 12

A = 30,6 см² A = 33,7 см²

I_x = 2900 см⁴ I_x = 1123 см⁴

I_y = 208 см⁴ I_y = 324 см⁴

z ₀ = 2,42 см I_{x (min)}=194 см⁴

х ₀=2,52см, y ₀=5,97 см

Рис. 21. Значения геометрических характеристик прокатных профилей:

а – швеллера № 24; б – неравнобокого уголка 180 x 110 x 12

Центробежные моменты инерции:

– для швеллера 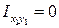(есть оси симметрии);

– для уголка ,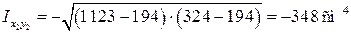

знак минус – в связи с положением уголка в сечении;

– для всего сечения:

.

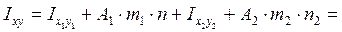
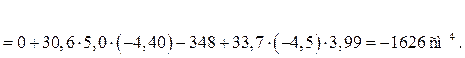
Проследите назначение знаков у n и m. От центральных осей швеллера переходим к общим центральным осям сечения, поэтому + m₂

и – n₂.

При переходе от осей x ₂ y ₂ к осям xy будет: – m ₂ и n ₂.

Главные моменты инерции сечения:

;

I_u = 5,53∙10³ cм⁴ = 5,53∙10^–5 м⁴;

I_v =1,6∙10³ cм⁴ = 1,6∙10^–5 м⁴.

Положение главных центральных осей сечения:

; α₀ = 55^о48^′;

α₀ = 27^о54^′.

Угол α₀ отсчитывается от оси x, так как I_x > I_y.

Проверка правильности вычисления величин I_u, I_v и α₀ производится по формуле

.

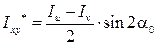Угол α₀ для этой формулы отсчитывается от оси u.

,

значит, операции по вычислению I_u, I_v, и α₀ произведены правильно.

Рассмотренное сечение имеет наибольшую сопротивляемость изгибу относительно оси u и наименьшую – относительно оси v.

Задача 5. Моменты инерции плоских сечений

Определить геометрические характеристики сечения (рис. 22), составленного из прокатных профилей (табл. 5).

План решения задачи:

1) определить положение центра тяжести;

2) найти величины осевых и центробежного моментов инерции относительно центральных осей;

3) вычислить величины главных центральных моментов инерции;

4) определить положение главных центральных осей инерции сечения;

5) вычертить сечение в масштабе 1: 2 и указать на нем все размеры в числах и все оси.

Рис. 22. Схемы к задаче 5

Таблица 5

Данные к задаче 5

Номер строки	Тип сечения	Номер швеллера	Равнобокий уголок	Номер двутавра
	I		80 х 80 х 8
	II		80 х 80 х 6
	III		90 х 90 х 8
	IV		90 х 90 х 7
	V		90 х 90 х 6	20а
	VI		100 х 100 х 8
	VII		100 х 100 х 10	22а
	VIII		100 х 100 х 10
	IX		125 х 125 х 10	24а
	X		125 х 125 х 12
	в	а	б	в

Вопросы для самоконтроля

1. По каким формулам определяются координаты центра тяжести сечения?

2. Для каких сечений при определении центра тяжести достаточно найти только одну координату?

3. Что называется осевым, центробежным и полярным моментами

инерции сечения?

4. Какова размерность моментов инерции?

5. Чему равен осевой момент инерции прямоугольника относительно

центральной оси параллельной основанию?

6. Относительно, каких центральных осей осевые моменты инерции

имеют наибольшее и наименьшее значения?

7. Запишите зависимость для осевого момента инерции при

параллельном переносе осей.

8. Как определяется положение главных осей?

Глава 6. ПЛОСКИЙ ИЗГИБ

Дата добавления: 2014-12-26