Пример 1. Определить площадь поперечных сечений на всех участках чугунного стержня (рис

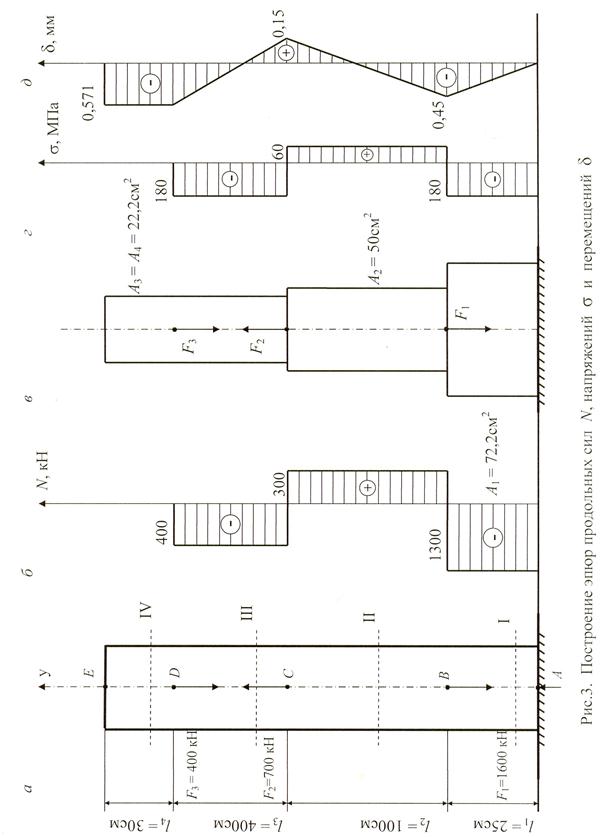
Определить площадь поперечных сечений на всех участках чугунного стержня (рис. 3, а). Построить эпюры продольных сил N, напряжений σ и перемещений δ. Принять для чугуна [σ_с] = 180 МПа, [σ_р] = 60 МПа, Е = 10⁵ МПа = 10¹¹ Па.

Рассматриваемый стержень имеет одну опорную реакцию R, и для него можно составить лишь одно уравнение статики: Σ Y = 0. Значит, эта система статически определима:

Σ Y = R – F ₁+ F ₂ – F ₃ = 0,

откуда R = 1300 кН.

Стержень подвергается растяжению – сжатию. Выделяем участки нагружения 1 – 4 (между точками приложения внешних сил), в пределах которых намечаются сечения I – IV.

Для определения N ₁ на первом участке рассмотрим равновесие части стержня, расположенной ниже сечения I – I. На нее действует реакция R (рис. 4). Уравнение статики Σ Y = 0 имеет вид

Σ Y = R + N ₁ = 0,

N ₁= – R = –1300 кН.

Полученный в результате подсчета знак минус при N ₁ указывает,

что N ₁ имеет направление, противоположное заданному, и что первый участок сжат.

Рис. 4. Определение внутренних сил N ₁

На часть стержня, расположенную ниже сечения II — II, действуют реакция R и сила F ₁. Тогда продольная сила в сечении II — II равна

N ₂ + R – F ₁= 0, N ₂ = – R + F ₁ = 300 кН.

Аналогично определяются N ₃, N ₄: N ₃ = – 400 кН; N ₄ = 0. По вычисленным значениям N строится эпюра продольных сил (см. рис. 3, б).

Из условия прочности 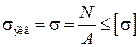определяем площади поперечных сечений на участках стержня:

A ₁ = м² = 72,2 см²;

;

.

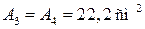Вычисления сделайте самостоятельно.

Рассчитываемый стержень с найденными площадями поперечных сечений показан на рис.3, в.

Нормальные напряжения:

; ; .

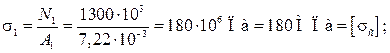
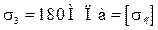Проделанные расчеты напряжений являются проверочными.

На рис. 3, г показана эпюра нормальных напряжений. Вычислим

деформации участков стержня:

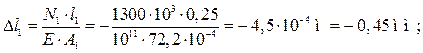
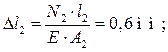
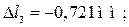
Перемещение любого сечения стержня равно сумме деформаций участков, расположенных между сечением и опорой.

Перемещение δ _А точки А: δ _А = 0. Перемещение точки В обусловлено деформацией участка I:

Перемещение точки С складывается из деформаций участков I и II:

Перемещение точки D складывается из деформаций участков I, II

и III:

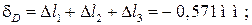
Перемещение точки E складывается из деформаций участков I, II, III

и IV:

По вычисленным значениям δ строится эпюра перемещений (см. рис. 3, д).

Задача 1. Растяжение и сжатие

(статически определимая система)

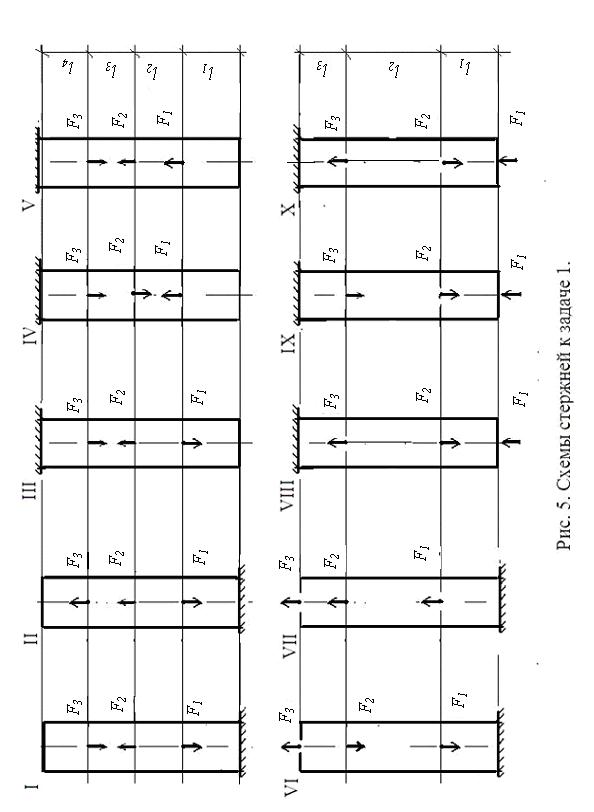
Произвести расчет стержня постоянного поперечного сечения (рис. 5) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением [σ], равным 210 МПа и модулем продольной упругости Е, равным 200 ГПа. Данные к задаче приведены в табл. 1.

План решения задачи:

1) вычислить продольные силы на участках стержня и построить эпюру N;

2) определить размеры поперечного сечения (сторону квадрата или диаметр);

3) вычислить нормальные напряжения на участках стержня и пос­троить эпюру σ по длине стержня;

4) вычислить деформацию участков стержня и построить эпюру перемещений δ.

Таблица 1

Данные к задаче 1

Номер строки	Номер схемы	Нагрузка, кН	Длина участков, см	Форма сечения
F 1	F 2	F 3	l1 , l4	l2	l3
	I							Круг
	II							Квадрат
	III							Круг
	IV							Квадрат
	V							Круг
	VI							Квадрат
	VII							Круг
	VIII							Квадрат
	IX							Круг
	X							Квадрат
	в	а	б	в	а	б	в	в

Дата добавления: 2014-12-26