Статически неопределимые системы

Системы, внутренние силы в элементах которых невозможно определить при помощи лишь одних уравнений статики, называются статически неопределимыми. Такие системы имеют «лишние» связи: внешние (опорные) или внутренние. Будем рассматривать только внешние ста­тически неопределимые системы.

Степень статической неопределимости определяется разностью между числом неизвестных реакций (связей) и числом независимых уравнений статики. Для раскрытия статической неопределимости к уравнениям статики нужно составить столько дополнительных уравнений, сколько раз статически неопределима система. Эти дополнитель­ные уравнения составляются из условий совместности деформаций.

Существуют несколько методов раскрытия статической неопределимости. Наиболее простой – метод сравнения перемещений (деформа­ций). Суть этого метода заключается в сравнении перемещений (деформаций) от заданной нагрузки и от реакции опоры в одностержневых системах и сопоставлении деформаций стержней в многостержневых системах. Раскрытие статической неопределимости для одиночных стержней, работающих на растяжение-сжатие, кручение и изгиб, однотипно. Для ведения расчета выбирается основная система, которая получается из заданной путем удаления лишних связей и, следовательно, является статически определимой (основная система, загруженная внешними силами и неизвестной реакцией, соответствующей удаленной связи, называется эквивалентной системой). Затем составляется дополнитель­ное уравнение, которое характеризует перемещение (деформацию) в сечении, где удалена связь.

Пример 2

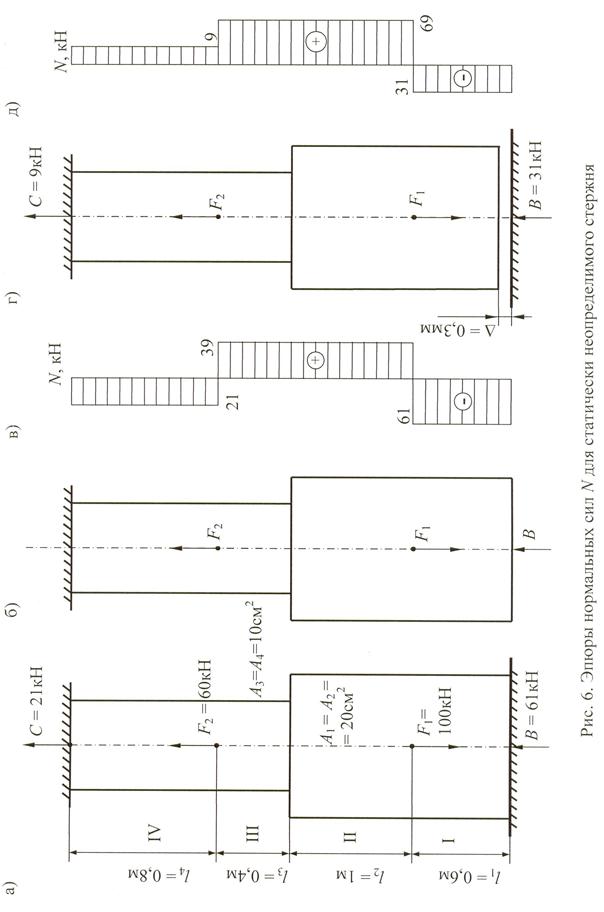
Раскрыть статическую неопределимость ступенчатого стержня, изготовленного из стали Ст3 (рис. 6, а) и построить эпюру продольных сил. Модуль упру­гости материала стержня Е равен 200 ГПа (прил. 3).

Стержень имеет две неизвестные опорные реакции С и В (направляем произвольно). Уравнение статики можно составить только одно:

Σ Y = С + F ₂ – F ₁ + В = 0.

Таким образом, система один раз статически неопределима. Основную систему получим, удалив связь, принадлежащую, например, опоре В. Эквивалентная система показана на рис. 6, б.

В сечении В заданной системы перемещение равно нулю. Значит, и в эквивалентной системе должно выполняться это условие δ _В = 0. Это и есть дополнительное уравнение. Для раскрытия его используем принцип независимости действия сил. Перемещение сечения В равно алгебраической сумме деформации всех участков стержня, вычисленных от каждой силы в отдельности.

Рассматривая эквивалентную систему, заметим, что реакция В сжимает все участки стержня, сила F ₁ растягивает участки II, III и IV_, а сила F ₂ сжимает участок IV.

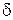_B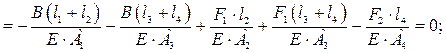

откуда В = 61·10³ Н = 61кН (направление совпадает с выбранным).

Опорную реакцию С определим из уравнения статики:

С + 60 – 100 + 61 = 0,

откуда С = – 21 кН (направление обратное).

Эпюра продольных сил N, построенная обычным образом (см. прим. 1), показана на рис. 6, в.

Опорную реакцию С можно определить аналогично реакции В, а уравнение статики – использовать для проверки правильности вычислений. Проделайте это самостоятельно.

Если рассматриваемый стержень вследствие неточности изготовления не будет достигать опоры на величину Δ (рис. 6, г), то дополнительное уравнение приметвид δ _В = Δ.Нарис. 6, д показана эпюра N при Δ = 0,03см.

Задача 2. Растяжение и сжатие

(статически неопределимая система)

Для бруса (рис. 7), изготовленного из стали 40, необходимо:

1) построить эпюры N, σ и δ;

2) определить запас прочности n.

Данные к задаче приведены в табл. 2.

Планрешения задачи:

1) определить степень статической неопределимости системы;

2) раскрыть статическую неопределимость системы (определяются опорные реакции);

3) построить эпюры N, σ и δ;

4) определить запас прочности из выражения .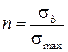

Таблица 2

Данные к задаче 2

Номер строки	Номер схемы	Нагрузка, кН	Площадь поперечного сечения, см^2	Зазор Δ, мм
F 1	F 2	А 1	А 2
	I					0,5
	II					0,4
	III					0,3
	IV					0,2
	V					0,3
	VI					0,1
	VII					0,2
	VIII					0,3
	IX					0,4
	X					0,5
	в	в	а	б	в	б

Вопросы для самоконтроля

1. Что называется эпюрой внутреннего усилия и для чего она строится?

2. Какое правило знаков принято для продольной силы?

3. Как вычисляют нормальные напряжения в поперечном сечении растянутого стержня?

4. Что называется абсолютным и относительным удлинением и какова их размерность?

5. Как формулируется закон Гука?

6. Какие системы называют статически неопределимыми? Каков

порядок их решения?

7. Как записывается условие прочности растянутого стержня по

методу допускаемых напряжений?

8. Можно ли в сопротивлении материалов переносить силу по линии

ее действия?

9. Что называется пределами пропорциональности, упругости,

текучести, прочности и какова их размерность?

10. По какой эпюре можно найти опасное сечение?

11. В чем состоит расчет стержня на прочность и на жесткость?

Глава 3. НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ

Дата добавления: 2014-12-26