Управляющий элемент

Фильтр нижних частот

Идеальный фильтр нижних частот (ФНЧ) обладает прямоугольной амплитудно-частотной характеристикой (АЧХ) (рис. 3.11).

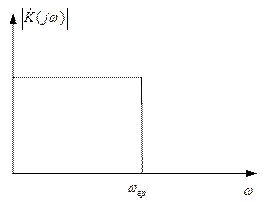
Рис. 3.11. Идеальная АЧХ ФНЧ

Примером элементарного реального ФНЧ может служить простейшая RC-цепочка (рис. 3.12).

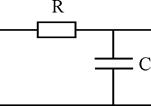
Рис. 3.12. RC-цепочка

Коэффициент передачи RC-цепочки

,

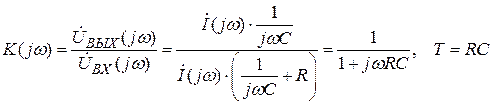или

.

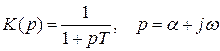ФНЧ в схеме ЧАП выполняет весьма важные функции. Он обеспечивает очищение полезных воздействий от шумов, а также требуемый астатизм и память системы при срыве слежения. Эти понятия будут рассмотрены дальше. АЧХ RC-цепочки при различных значениях постоянной времени изображена на рис. 3.13.

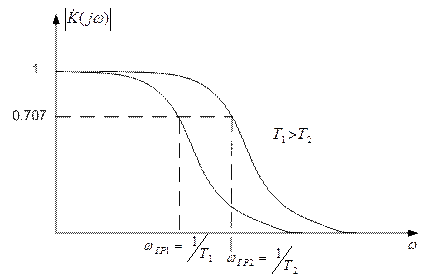
Рис. 3.13. АЧХ RC-цепи

Обычно это реактивный элемент, входящий в состав резонансного контура управляемого автогенератора и обладающий емкостным или индуктивным сопротивлением, изменяющимся под воздействием приложенного к этому элементу напряжения. Самым простым таким элементом является варикап.

Работа управляющего элемента характеризуется управляющей или регулировочной характеристикой. Регулировочной характеристикой управляющего элемента называют зависимость изменения частоты управляемого генератора 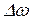от приложенного к управляющему элементу напряжения. Это напряжение снимается с выхода ФНЧ и, как правило, является медленно изменяющимся.

На рис. 3.14 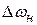– начальная расстройка или неточность настройки автогенератора, имеющая место в схеме к моменту начала регулирования.

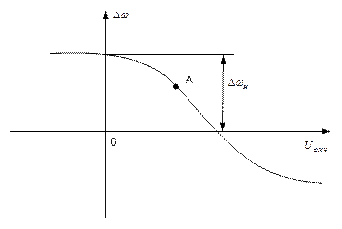
Рис. 3.14. Регулировочная характеристика УЭ

Теперь, когда рассмотрены схемы и функции основных элементов, входящих в схему ЧАП, напомним еще раз элементарный принцип ее действия (рис. 3.15). Основной задачей схемы является обеспечение быстрого стремления 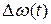к нулю. Достигается это следующим образом. Дискриминатор на своем выходе вырабатывает напряжение, пропорциональное величине 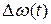. Знак этого напряжения зависит от знака 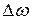. Возникшее напряжение фильтруется в ФНЧ, где очищается от шумов, далее воздействует на управляемый генератор и изменяет его частоту так, чтобы на выходе смесителя 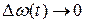, т.е. .

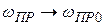Таким образом, в схеме реализуется отрицательная обратная связь по частоте.

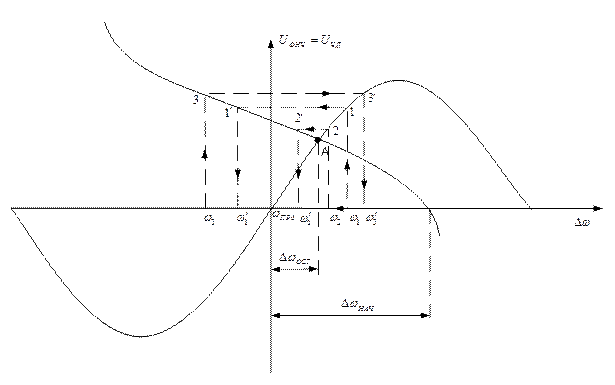
Рис. 3.15. Графики регулированной и дискриминационной характеристик

Поясним дополнительно физическую сущность процесса регулирования, используя графики дискриминационной и регулировочной характеристик, объединив их в одном чертеже. Считаем при этом для упрощения, что ФНЧ отсутствует и выход дискриминатора подключен непосредственно ко входу регулировочного элемента. Пусть в силу каких-либо причин частота управляемого генератора приняла значение 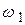. Тогда напряжение на выходе частотного дискриминатора примет значение, соответствующее точке 1. Это же напряжение воздействует на регулировочный элемент (точка 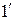), которому по регулировочной характеристике соответствует частота 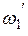. Частота управляемого генератора будет стремиться принять это значение 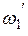, однако, приняв в процессе регулирования значение 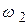под воздействием возникшего напряжения на выходе дискриминатора (точки 2, 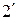), эта частота будет стремиться принять значение 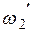. Остановится процесс регулирования в точке пересечения дискриминационной и регулировочной характеристик. Аналогичный процесс изменения частоты будет иметь место, если она в силу каких-либо причин примет значение 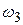справа. Процесс изменения частоты также завершится в точке пересечения дискриминационной и регулировочной характеристик. Остаточная расстройка частоты 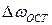будет рана нулю лишь тогда, когда будет равной нулю начальная расстройка 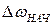. Остаточная расстройка свойственна астатическим системам, которые будут рассмотрены в разд. 4. Величину этой расстройки можно уменьшить, либо увеличив крутизну дискриминационной и регулировочной характеристик, либо повысив порядок астатизма схемы.

Структурная схема модели системы ЧАП

Из сказанного ранее следует, что основным параметром, который нас интересует в данной схеме, является частота. Поэтому имеет смысл рассмотреть схемную модель системы ЧАП, но не для исследования поведений напряжений, а для исследования поведения частоты.

Эта схема показана на рис. 3.16. Рассмотрим функции каждого из ее элементов.

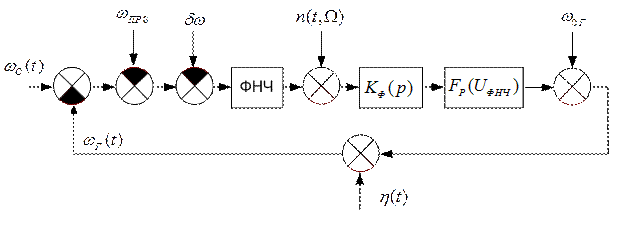Рис. 3.16.Структурная схема модели системы ЧАП

Входным сигналом (воздействием) схемы является не напряжение, а частота. Первый элемент в этой модели системы ЧАП моделирует смеситель и выполняет операцию вычитания частот:

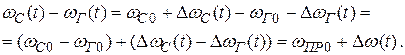
Для пояснения следующих операций рассмотрим рис. 3.17.

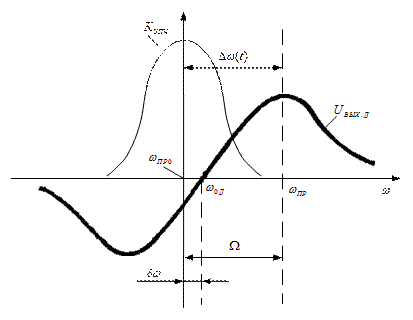
Рис. 3.17. Неточность настройки частот 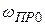и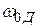

Здесь 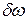– неточность настройки центральной частоты УПЧ 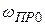и центральной частоты дискриминатора 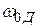. В идеальном случае должно быть совпадение этих частот, т.е. 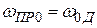. Ω – расстройка относительно центральной частоты дискриминатора. Именно эта частота приводит к появлению на выходе дискриминатора напряжения, которое, пройдя через ФНЧ и воздействуя на регулировочный элемент, управляет работой управляемого автогенератора. Эта частота, как видно из рисунка, равн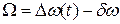а , а 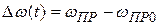. Поэтому прежде чем исследовать в схеме непосредственное воздействие на дискриминатор частоты Ω, необходимо из промежуточной частоты вычесть частоты 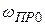и 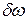. F(Ω) – дискриминационная характеристика частотного дискриминатора. При отсутствии шумов – это зависимость 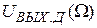, т.е. 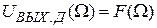. В случае наличия шумов – это зависимость математического ожидания выходного напряжения от :

.

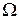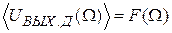Далее в этой схемной модели (см. рис. 3.16) после дискриминатора размерность воздействий – напряжение.

Как правило, на вход системы ЧАП полезный сигнал поступает в смеси с шумом. Этот шум проходит входные цепи, УПЧ, а затем поступает в дискриминатор. Дискриминатор, как видно по его характеристике, является нелинейным устройством. Шум, пройдя через это нелинейное устройство, претерпевает сложные изменения и становится зависимым не только от времени 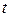, но и от частоты Ω. Этот шум целесообразно исследовать и включить с соответствующими статистическими характеристиками в виде некоторого автономного источника в схемную модель на выходе дискриминатора.

Напряжение с выхода дискриминатора и шум поступают в фильтр (характеризующийся коэффициентом передачи 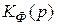), где осуществляется обработка смеси полезного напряжения и шума. Обработка может быть как простой, так и сложной, требующей цифровых фильтров. Выходное напряжение фильтра воздействует на регулировочный элемент и управляет частотой автогенератора. Регулировочный элемент характеризуется регулировочной характеристикой 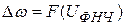, а регулировочная характеристика – крутизной .

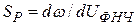Изменение частоты на выходе УГ

.

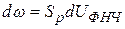На линейном участке регулировочной характеристики

.

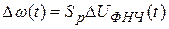К этим изменениям частоты в схемной модели необходимо добавить рабочую частоту управляемого автогенератора 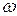_0Г, а также его нестабильность 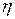(t), являющуюся функцией времени. Таким образом,

.

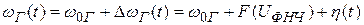В схеме ЧАП основной интерес представляет исследование изменений частоты 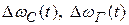и 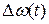. Причем необходимо, чтобы 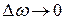. Другими словами, в схеме имеет смысл рассматривать лишь те слагаемые в выражениях для частот 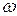_Г(t) и 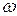_C(t), которые изменяются во времени. Поскольку в схеме 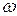_Г0 и 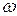_C0 не изменяются, то для упрощения схемы их можно исключить. Тогда упрощенная схема будет иметь вид, изображенный на рис 3.18.

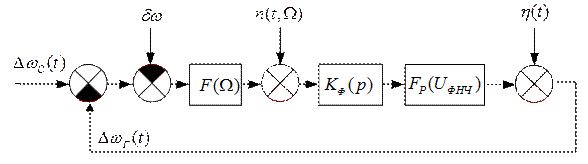Рис. 3.18. Структурная схема модели системы ЧАП по отношению

к приращениям частот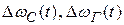

Однако и эта схема является сложной для анализа. Поэтому для того чтобы исследовать схему с наибольшим пониманием происходящих в ней процессов как процессов управления, введем еще ряд упрощений.

1. Предположим, что частоты настройки УПЧ и дискриминатора совпадают, т.е. δ 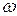=0.

2. Так как схема нормально выполняет свои функции, когда изменение частоты происходит в пределах линейного участка дискриминационной характеристики, то полагаем, что 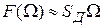, где .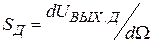

3. Крутизна регулировочной характеристики 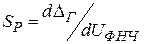может быть включена в фильтр 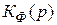как постоянный коэффициент (например коэффициент усиления). Обозначим .

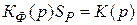4. Пересчитаем случайный процесс 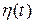на вход фильтра 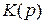и объединим его с процессом 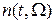. Обозначим новый процесс 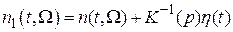. Учесть это в полном объеме в схеме достаточно сложно, поэтому для упрощения дальнейшего анализа можно считать, что процесс 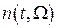является белым шумом с корреляционной функцией 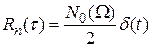. Далее будет рассмотрен еще более простой случай, когда шум 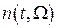не зависит от Ω, т.е. , .

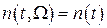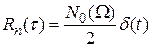С учетом всех этих упрощений схема примет такой вид (рис. 3.19).

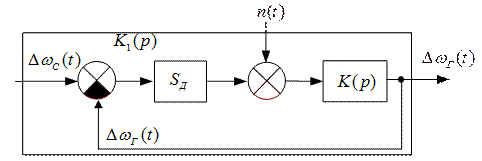а

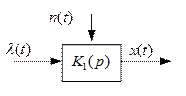б

Рис. 3.19. Упрощенная структурная схема модели системы ЧАП: а – расширенная структурная схема модели системы ЧАП; б – представление модели системы ЧАП в виде фильтра

Полученная упрощенная структурная схема модели системы ЧАП позволяет, несмотря на ее простоту, подробно изучить процесс слежения за изменением частоты принимаемого сигнала .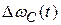

Дата добавления: 2014-12-26