Построение переходной матрицы

1. Запишем переходную матрицу в виде

,

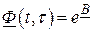где

.

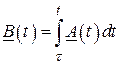Как уже отмечалось, матричная экспонента представляется рядом

.

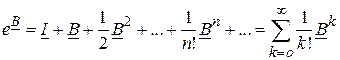Первый способ построения переходной матрицы заключается в непосредственном вычислении этого ряда, который ограничивается 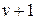слагаемым. Если некоторая 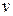степень матрицы 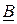равна нулю, т.е. 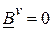, такие матрицы называются нильпотентными.

В линейной алгебре доказывается следующий факт. Если некоторая функция 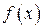, где 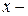действительная переменная, определена на спектре матрицы 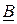(принимают определенные значения сама функция и ее производные при 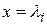, где 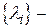совокупность собственных чисел – спектр матрицы 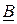) и если удается подобрать полином 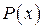, определенный на этом спектре и принимающий в точках 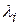те же значения, что и функция 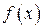, т.е. 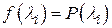, то функция и полином, рассматриваемые как функции матрицы 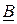, совпадают:

.

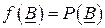Более того, любые функции, определенные на спектре матрицы 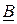и принимающие на нем одинаковые значения, совпадают, если они рассматриваются как функции этой матрицы:

.

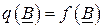Формула (2.96) называется формулой Лагранжа – Сильвестра, а полином 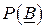– интерполяционным полиномом Лагранжа – Сильвестра. Это означает, что функция 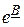, представленная бесконечным рядом, может быть заменена полиномом как функцией матрицы 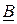с конечным числом слагаемых.

Интерполяционный полином Лагранжа – Сильвестра можно составить следующим образом.

Пусть известны матрица 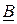, например размерностью 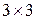, с собственными числами 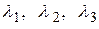, а также некоторая функция 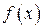, определенная на этом спектре, например функция 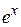, имеющая значения 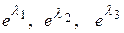. Такие же значения 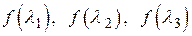принимает полином

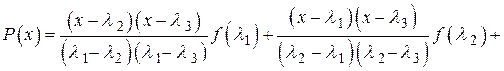
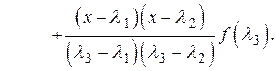
Действительно, легко убедиться, что

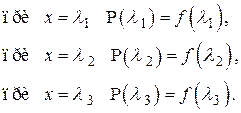
В соответствии с формулой Лагранжа – Сильвестра

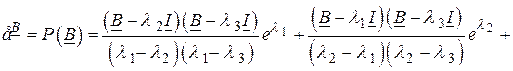
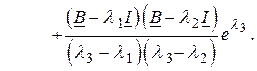
Таким образом, переходную матрицу состояния можно получить, суммируя не бесконечное число слагаемых, как в (2.94), а всего три слагаемых.

2. Пусть матрица 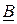приводится к диагональному виду, т.е. существует матрица :

.

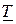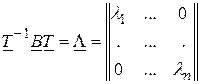Тогда имеют место формулы, аналогичные (2.88) – (2.90):

.

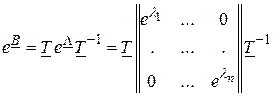Основные трудности построения матрицы 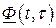в соответствии с пп. 1 – 3 (см. с. 34) связаны с тем, что матрица 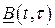зависит от переменных 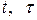, т.е. все указанные условия изменяются в соответствии с изменением этих двух аргументов.

3. Для стационарных систем матрица . Поскольку и переходная матрица зависит от разностного аргумента, тогда, не уменьшая общности, можно принять начальный момент времени 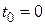. Так как

,

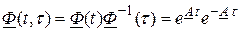то достаточно найти 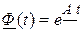. Эту функцию проще получить, решая дифференциальное уравнение (2.71) для фундаментальной матрицы методом преобразований Лапласа

,

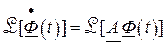или

.

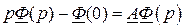Здесь 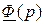– изображение функции 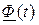, , 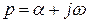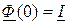- значение оригинала при 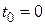(начальное условие). Решая алгебраическое матричное уравнение, получаем

,

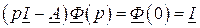откуда

.

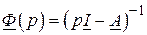Искомую фундаментальную матрицу 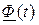находим путем применения к матрице 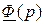обратного преобразования Лапласа:

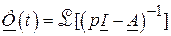
(элементы матрицы 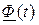находят путем обратного преобразования Лапласа к каждому элементу матрицы ).

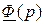Дата добавления: 2014-12-26