Метод дифференциальных уравнений

Этот метод применим для исследования стационарных и нестационарных систем в установившемся и переходном режимах с учетом начальных условий. Входные воздействия могут иметь стационарный и нестационарный характер, быть как регулярными, так и случайными. Метод в значительной степени универсален. Однако во многих случаях по простоте использования он уступает методам преобразований Фурье и Лапласа, например, при изучении стационарных линейных систем.

В соответствии с этим методом работу схемы фильтрации, показанной на рис. 2.1, можно описать дифференциальным уравнением вида

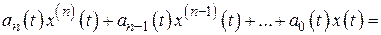
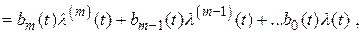
где

.

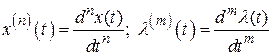Введем символическую запись оператора :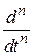

.

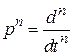Тогда дифференциальное уравнение (2.16) запишется так:

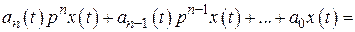
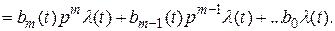
Формально функци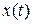и и 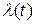можно вынести вправо [1, 2]:

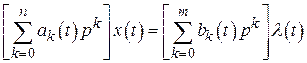
и записать

,

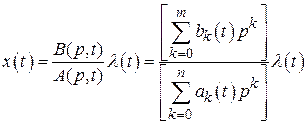где

;

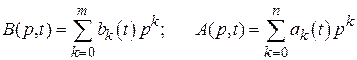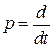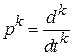, – линейные дифференциальные операторы.

С учетом этих обозначений можно записать дифференциальное уравнение (2.16) в компактной форме:

,

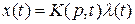где .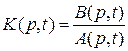

Дополнительно необходимо учесть такие начальные условия:

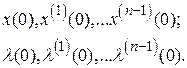
Система, описываемая дифференциальным уравнением (2.16), является линейной нестационарной. Признак нестационарности системы – зависимость от времени коэффициентов 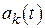. Для стационарной системы дифференциальные уравнения (2.16) и (2.22) примут следующий вид:

.

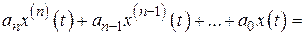
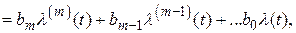
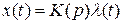Для нахождения отклика 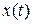необходимо решить уравнения (2.16), (2.18) или (2.20), (2.22) при заданных начальных условиях (2.23).

Одним из таких методов является метод преобразований Лапласа. Применим к дифференциальному уравнению (2.16) прямое преобразование Лапласа. Для функции 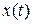и ее производных изображения Лапласа будут иметь вид

,

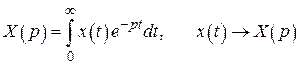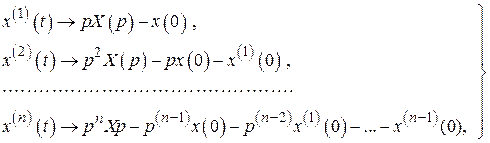
где 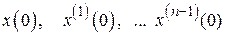– начальные условия.

Аналогичные соотношения имеют место для функции и ее производных.

Подставив эти соотношения в уравнение (2.24), получим

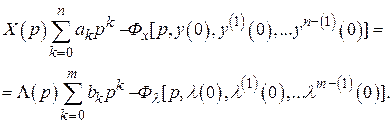
Изображение отклика на выходе системы равно

,

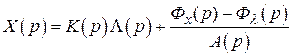где

.

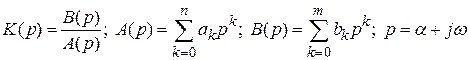Отметим подобие формул (2.25) и (2.28) (с точностью до слагаемого, содержащего начальные условия). Различие состоит в том, что в формуле (2.25) 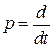, а в (2.28) 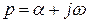. В формуле (2.25) 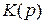– линейный оператор, примененный к функции 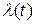, а в (2.28) 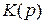- передаточная характеристика фильтра.

Таким образом, по внешнему виду линейного оператора 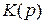, представляющего собой дифференциальное уравнение (2.24), можно определить передаточную характеристику фильтра, заменив 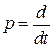на .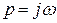

Отклик линейной системы 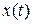находим, применяя к изображению 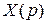обратное преобразование Лапласа:

.

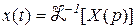Все рассмотренные методы связаны между собой. Передаточные 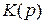, 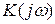и импульсная 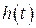характеристики связаны между собой преобразованиями Фурье и Лапласа, а с коэффициентами дифференциального уравнений (2.16), (2.24) - соотношениями (2.21), (2.29).

Отметим также, что поскольку для нестационарных систем коэффициенты 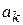, 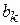дифференциального уравнения (2.16) зависят от времени, то импульсная характеристика будет зависеть от момента подачи импульса и иметь вид 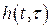, т.е. импульсная характеристика будет зависеть не от разностного аргумента 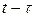, а от каждой переменной 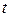, 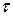отдельно. Соответственно функциями времени будут являться и коэффициенты передачи 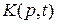, 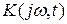. Последние требуют корректного к ним отношения, так как интегрирование в преобразованиях Фурье и Лапласа осуществляется в бесконечных пределах.

Дата добавления: 2014-12-26