Метод пространства состояний

Этот метод широко применяется в современных системах для решения задач оптимальной фильтрации с помощью цифровых фильтров и ЭВМ и имеет преимущества по сравнению с другими методами при фильтрации нестационарных процессов, а также при использовании нестационарных систем. В простейшем случае сущность метода заключается в замене дифференциального уравнения n-го порядка системой из n уравнений первого порядка, искомые переменные которой при описании динамических систем называют состояниями.

Рассмотрим два способа описания системы фильтрации в пространстве состояний.

I. Пусть 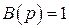. Коэффициент передачи

.

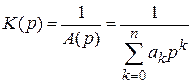Для простоты полагаем также, что . В этом случае дифференциальное уравнение (2.24) примет следующий вид:

.

Если коэффициент , то на него можно разделить знаменатель и числитель и ввести новые коэффициенты 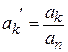. Тогда

,

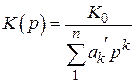где 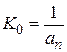рассматривается как постоянный коэффициент передачи дополнительного четырехполюсника, входящего в состав фильтра 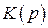. Этот коэффициент всегда можно учесть в конечном результате фильтрации, и поэтому без потери общности целесообразно рассматривать выражение (2.31).

В развернутой форме дифференциальное уравнение, соответствующее коэффициенту передачи (2.31), не содержит в правой части производных от функции :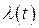

.

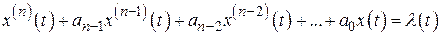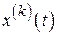Обозначим функцию и производные такими переменными:

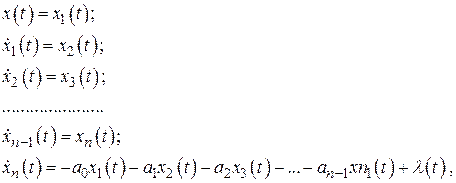
где .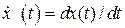

Запишем эту систему дифференциальных уравнений первого порядка в векторно-матричной форме

,

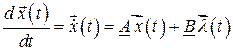или

где вектор 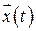имеет размерность 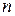, матрица 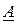– размерность 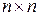, матрица 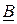– размерность n 1, вектор – размерность, равную единице.

Переменные 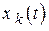называют состояниями системы, или ее фазовыми координатами (переменными).

Для фильтра, описываемого операторным коэффициентом передачи (2.31) или системой уравнений (2.34), интересующей нас переменной чаще всего является функция 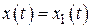, т.е. первая фазовая координат этой системы.

В случае, когда 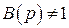, т.е.

,

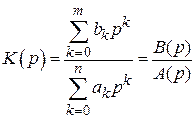и в правой части дифференциального уравнения стоят производные от входного воздействия 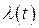, задача приведения дифференциального уравнения к векторно-матричному виду сложнее. Введем промежуточную переменную

.

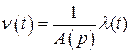Тогда

.

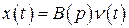Дифференциальное уравнение (2.38) относительно переменной 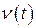содержит операторный коэффициент передачи (2.31) и аналогично уравнению (2.32). В векторно-матричной форме уравнение (2.38) запишется так же, как и уравнение (2.35):

,

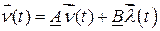где

.

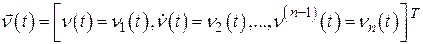Искомую функцию находим путем дифференцирования функции 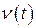, применяя дифференциальный оператор :

.

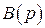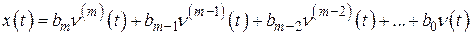Последнее равенство можно записать в векторно-матричной форме

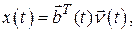
если ввести вектор 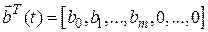размерностью n.

II. Второй способ представления дифференциального уравнения в векторно-матричной форме заключается в следующем.

Запишем дифференциальное уравнение

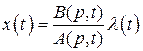
в развернутом виде

.

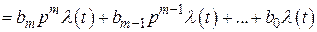Разделим обе части уравнения на величину и решим уравнение относительно функции :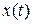

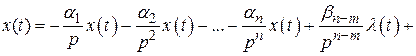
где

Рассматривая оператор 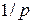как интегральный, составим схемную модель фильтра, описываемого дифференциальным уравнением (2.41) (рис. 2.6).

Рис. 2.6. Модель фильтра, описываемого дифференциальным уравнением

В качестве переменных состояния примем значения процессов на выходах интеграторов в составе схемы. Нумерацию этих переменных начинаем с последних каскадов:

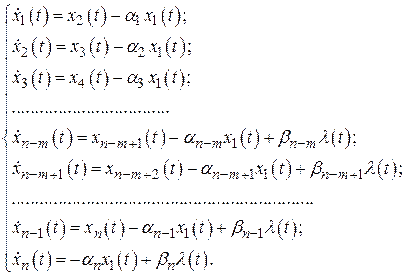
В векторно-матричной форме эта система дифференциальных уравнений первого порядка будет иметь следующий вид:

,

или

.

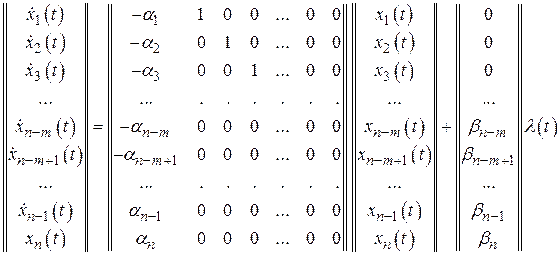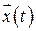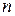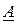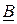Здесь размерность вектора равна , матрицы – n n, матрицы – n 1 и вектора – 1.

В общем случае многомерной нестационарной системы (рис. 2.7), когда на ее входах действуют 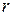регулярных и 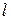случайных процессов, уравнение состояния в векторно-матричной форме запишется так:

.

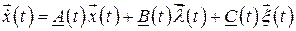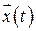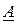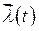В этом уравнении вектор имеет размерность n, матрица –размерность n n, вектор – размерность 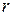, матрица 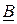равна n 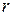, вектор 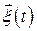– размерность 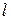и матрица 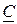– размерность n 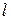. Единственное решение имеет место, если заданы начальные условия .

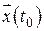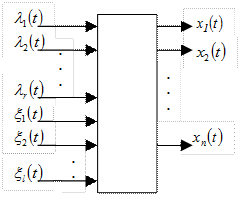
Рис. 2.7. Многомерная система

При исследовании динамических систем и фильтров в пространстве состояний оценке подлежат координаты вектора 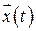, т.е. состояния системы. При этом следует учитывать то, что эти координаты наблюдаются в шумах и через связи, которые заданы в виде уравнения наблюдения

,

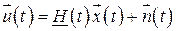где матрица 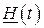имеет размерность k n, векторы 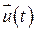и 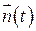– размерность k. Например, пусть имеем скалярный процесс

.

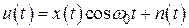Здесь – амплитуда, подлежащая оценке. Амплитуда рассматривается как фазовая переменная (состояние) некоторого формирующего фильтра; 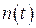– помеха; .

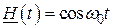Имея уравнение состояния системы и наблюдения, легко составить схемную модель, удовлетворяющую этим условиям (рис. 2.8).

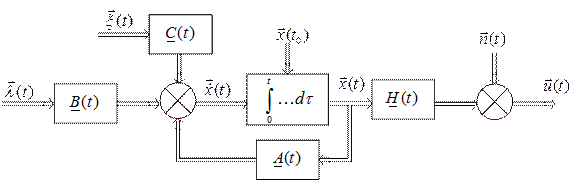Рис. 2.8. Схемная модель системы и уравнение наблюдения в пространстве состояний

Прежде чем решить векторно-матричное дифференциальное уравнение (2.46), решим простое скалярное дифференциальное уравнение первого порядка:

.

Общее решение этого уравнения состоит из суммы общего решения однородного уравнения

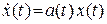
и частного решения 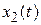, соответствующего внешним воздействиям и :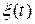

.

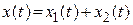При заданном начальном условии 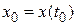общее решение однородного уравнения становится частным. Оно обусловлено наличием в системе лишь этого начального условия (для электрической схемы – начального заряда или тока).

Решение однородного уравнения находим методом разделения переменных. Запишем (2.50) в виде

.

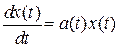Разделим переменные:

.

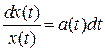Проинтегрируем полученное уравнение:

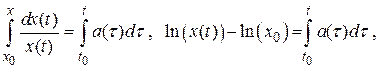
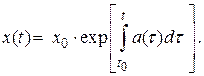
В том случае, если уравнение (2.50) описывает стационарную систему, то и

.

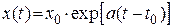Введем функцию

.

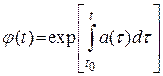Эта функция также является решением дифференциального уравнения (2.50) при 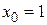. Продифференцируем эту функцию:

.

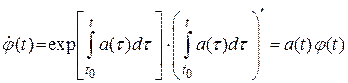Очевидно, что эта функция удовлетворяет уравнению (2.50) и является одним из его решений. Заметим, что .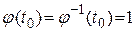

Таким образом, имеем

.

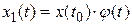Частное решение дифференциального уравнения (2.49) при наличии внешних воздействий на систему 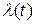и 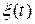ищем методом вариации произвольных постоянных, т.е. представляем это решение в виде, подобном (2.55), но с множителем 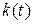, зависящим от времени (внешние воздействия как бы изменяют начальный заряд ):

.

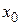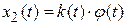Это решение должно удовлетворять уравнению (2.49), т.е. превращать его в тождество. Подставив его в (2.49), получаем

.

Принимая во внимание выражение (2.54) и подставляя его в это уравнение, имеем

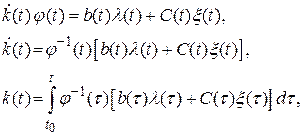
а

.

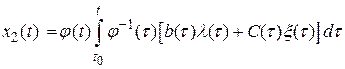Внесем 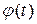под знак интеграла и обозначим произведение:

.

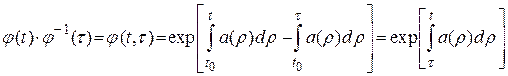Суммарное решение (2.51) примет такой вид:

.

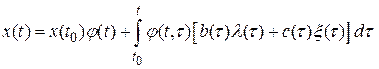Умножим первое слагаемое на функцию 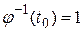. От этого ничего не изменится, но функцию 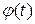, как и функцию (2.56), можно будет представить в виде .

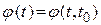Тогда

.

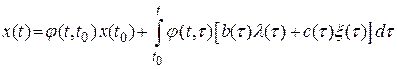В соответствии с методом импульсных характеристик здесь по отношению ко входам, на которые действуют процессы 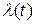и 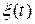, импульсные характеристики имеют вид

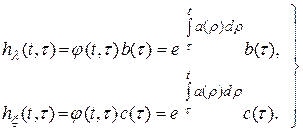
Для линейных систем 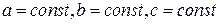. Тогда

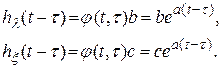
Решение векторно-матричного уравнения ищем, следуя той же методике, которая выше была применена к решению скалярного уравнения (2.49).

Дата добавления: 2014-12-26