Метод преобразований Лапласа

Метод преобразований Лапласа также позволяет найти отклик на выходе линейной динамической системы. Он, в частности, применим тогда, когда условие не выполняется. Преобразованиями Лапласа называют интегралы

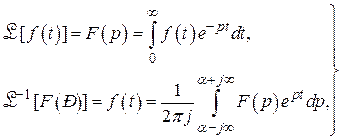
где 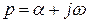; – константа; 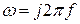– круговая частота. Исходную функцию 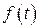, которую подвергают прямому преобразованию Лапласа, называют оригиналом, а функцию 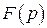– изображением функции 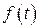. Восстанавливается функция 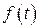путем применения к 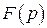обратного преобразования Лапласа.

Ценностью преобразований Лапласа является то, что ему могут поддаваться функции, не удовлетворяющие условию. Это можно показать следующим образом. Учитывая, что 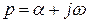, запишем прямое преобразование Лапласа в таком виде:

.

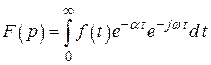Здесь преобразование Фурье применяется к функции 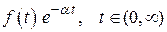. Экспонента 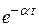- одна из наиболее быстро спадающих функций, которая существенно снижает рост функции 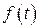(рис. 2.3). Тогда интеграл сходится, т.е.

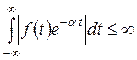
В этом случае при взятии этого интеграла обычно не возникает проблем. Следует отметить, что преобразование Фурье от ряда функций, не удовлетворяющих условию (2.2), можно найти, предварительно вычислив преобразование Лапласа и положив затем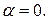

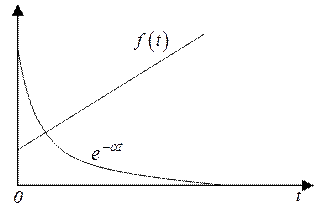
Рис. 2.3. Снижение роста функции 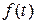функцией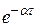

Линейные стационарные системы можно исследовать методом преобразований Лапласа следующим образом. Если при заданном входном воздействии требуется определить выходное, то в этом случае следует действовать в такой последовательности:

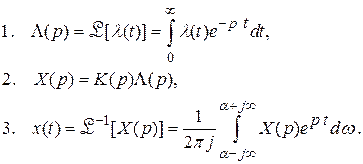
Возможны решения и других задач, указанных при рассмотрении метода Фурье.

На рис. 2.4 показаны типичные входные воздействия: .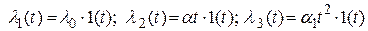

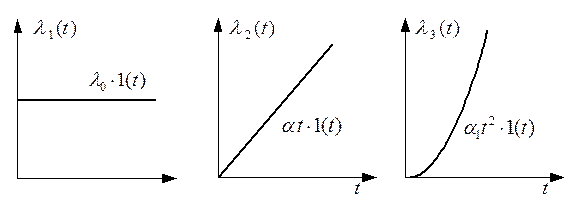
а б в

Рис. 2.4. Типичные входные воздействия

Для них образы Лапласа соответственно равны

.

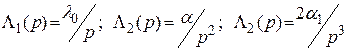Положив 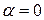, получим образы Фурье

.

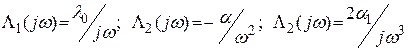Амплитудные спектры, как видим, имеют особенность при 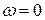(равны бесконечности).

Дата добавления: 2014-12-26