Переходная матрица системы

Решение векторно-матричного дифференциального уравнения.

Рассмотрим сначала однородное уравнение

.

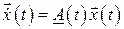Решение ищем в виде

.

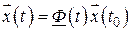Подставив (2.60) в (2.47), получаем

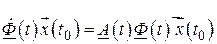
или

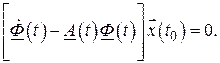
Так как вектор 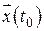, характеризующий начальные условия, может принимать произвольные значения в некоторой области значений, то неизвестная функция (2.60) должна удовлетворять матричному дифференциальному уравнению

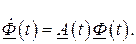
Следует отметить, что выражение (2.60) должно быть справедливым в начальный момент времени 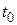, т.е.

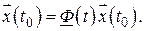
Это возможно в том случае, когда

,

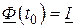где 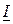– единичная матрица.

Условие (2.62) является начальным для решения дифференциального уравнения (2.61).

Аналогично тому, как для простейшего скалярного уравнения с разделяющимися переменными 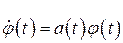решением есть функция

,

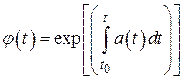решением матричного уравнения является матрица

,

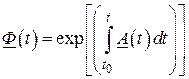где

.

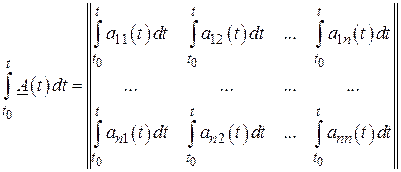Тогда частным решением однородного векторно-матричного уравнения (2.59) будет вектор (см. (2.60))

.

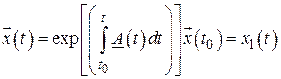Матрицу 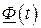называют фундаментальной матрицей решений однородной системы уравнений (1.47). Если элементы матрицы 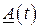– постоянные величины, то

.

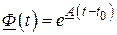Эту матрицу называют матричной экспонентой.

Наглядный смысл функция 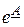имеет, если представить ее, как и обычную экспоненту от скалярной переменной, в виде ряда

.

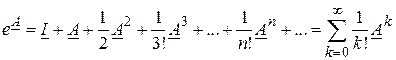Отметим такие свойства матричной экспоненты:

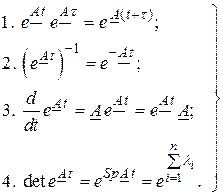
Если 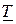– невырожденная матрица, то

.

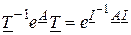что легко проверяется подстановкой (2.68) в (2.66). Если матрица 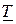приводит матрицу 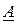к диагональному виду, т.е.

,

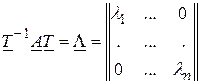то

.

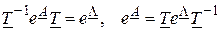Здесь 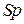– след матрицы (сумма диагональных элементов); 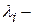собственные числа матрицы .

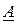Частное решение неоднородного дифференциального уравнения (2.46) находим методом вариации произвольных постоянных, т.е. в виде (2.65), заменив вектор 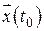на неизвестную векторную функцию :

.

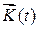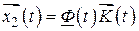Так как по предположению этот вектор является решением уравнения (2.46), то функцию 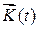находим подстановкой вектора (2.71) в уравнение (2.46):

.

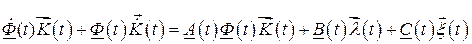Заметим, что производная от матрицы 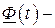матрица 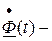состоит из элементов, равных производным от элементов матрицы 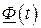. Подставляя в левую часть этого равенства вместо матрицы 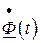правую часть уравнения (2.61) и сокращая в обеих частях равенства (2.72) первые слагаемые, имеем

.

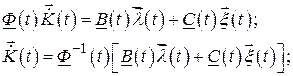
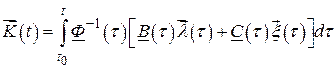Подставляя последнее равенство в выражение (2.71), получаем частное решение неоднородного уравнения (2.46):

.

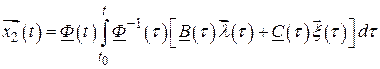Полное частное решение неоднородного уравнения равно сумме частного решения однородного уравнения и полученного выше частного решения неоднородного уравнения:

.

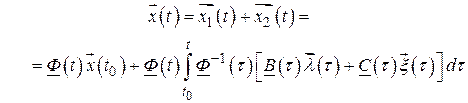Введем функцию

.

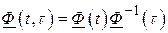В слагаемом, соответствующем частному решению уравнения (2.59), вместо матрицы 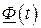введем равную ей матрицу :

.

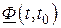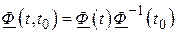Так как (см. (2.62))

,

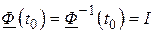то

.

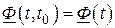Тогда

.

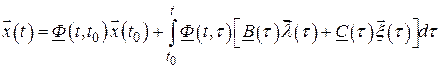Функцию 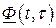называют переходной матрицей состояния

.

В литературе эту матрицу называют также фундаментальной матрицей решений однородной системы уравнений (2.59), нормированной фундаментальной матрицей, матрицей Грина, матрицей Коши, нормированной интегральной матрицей, резольвентным ядром. Матрицы 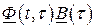и служат матричными аналогами импульсных характеристик системы и называются импульсными переходными, или весовыми матрицами.

Как отмечалось, импульсные характеристики являются реакциями системы на импульсы, имеющие вид дельта-функций.

Введем такие обозначения:

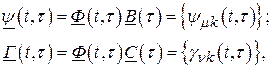
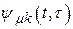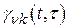где и – элементы матриц 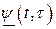и 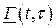; 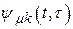– отклик многомерной системы (см. рис. 2.7) на -м выходе при подаче на

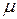-й вход вместо функции 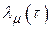импульса в виде дельта-функции 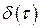; 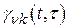– отклик на -м выходе системы (см. рис. 2.7) при подаче на ее вход дельта-импульса вместо функции .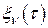

Для многомерного формирующего фильтра, описываемого дифференциальным уравнением

,

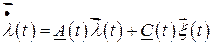имеем решение

.

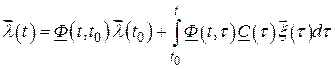Для стационарного фильтра

.

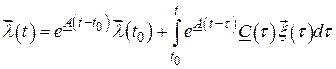Свойства переходной матрицы такие:

1. .

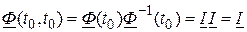2. .

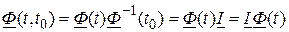3. .

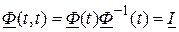4. .

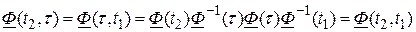5. .

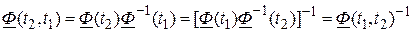6. Переходная матрица удовлетворяет дифференциальному уравнению

.

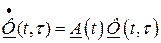7. Детерминант матрицы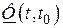

.

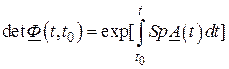8. Для стационарной системы (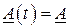) имеют место следующие свойства:

,

.

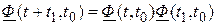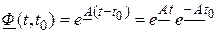В п. 5 использовано известное свойство матриц

.

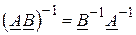При выводе дифференциального уравнения в п. 6

.

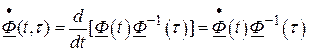Учитывая, что фундаментальная матрица 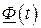удовлетворяет дифференциальному уравнению (2.51), получаем

.

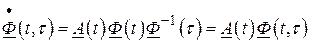Начальным условием этого уравнения является .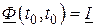

Из п. 8 следует, что достаточно вычислить 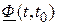при 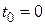, т.е. 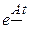. В целях получения матрицы 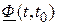для стационарной системы достаточно заменить в матричной экспоненте 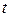на .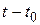

Дата добавления: 2014-12-26