В дискретной форме

Представление решений дифференциальных уравнений

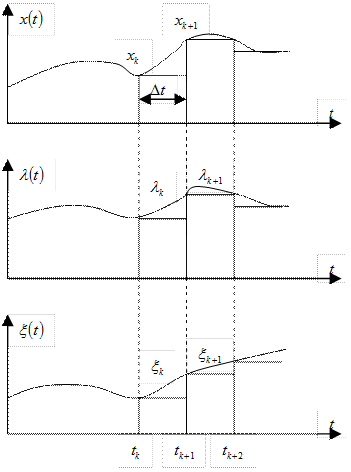
Рассмотрим рис. 2.9. На оси времени отмечены точки 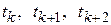, следующие через интервалы времени 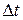. Сначала считаем, что на интервалах дискретизации функци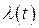и и 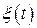постоянны. Например, на интервале времени (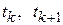) функци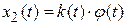и и 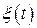равны соответственно 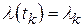и 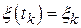. Если предположить, что искомая функция 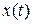в момент времени 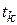известна (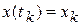), то это значение можно принять в качестве начального условия и искать решение дифференциального уравнения 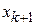в момент 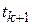в соответствии с формулой (2.70):

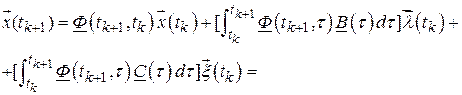
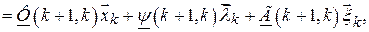
где

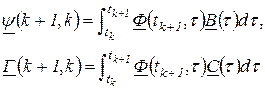
переходные матрицы по входам поступления воздействи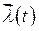й и 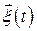соответственно.

Эти выражения проясняют смысл «переходная матрица», так как позволяют перейти от известного значения (начального условия) 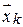в момент времени 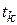к искомому значению 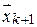в момент времени .

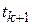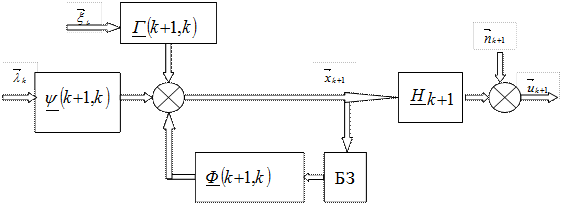
Схема, соответствующая решению (2.103) с учетом уравнения наблюдения (2.47), показана на рис. 2.10 (БЗ – блок задержки на один шаг ).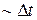

При достаточно малом интервале дискретизации 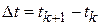все функции можно вынести за знаки интегралов:

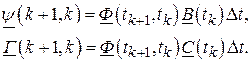
Тогда

,

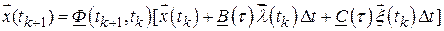или

.

  Рис. 2.9. Дискретизация воздействий

Рис. 2.10. Дискретная модель системы и уравнение наблюдения в пространстве состояний

Для стационарных систем

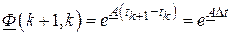
и

.

Для формирующего фильтра, на выходе которого имеем модуль процесса 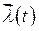, представленного решением (2.84), аналогично (2.103) имеем

.

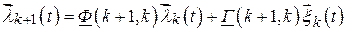При достаточно малом 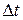для последовательностей 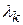имеют место формулы, аналогичные формулам (2.104), (2.105).

Нередко в теории фильтрации векторная случайная функция 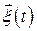рассматривается как совокупность процессов типа белого шума с ковариационной матрицей 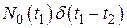и спектральными плотностями мощностей 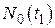(в общем случае эти белые шумы нестационарные). Такую функцию выносить за пределы интеграла нельзя ни при каком малом 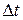. Все остальные функции при достаточно малом интервале 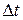можно вынести за знаки интегралов. Тогда

,

или

,

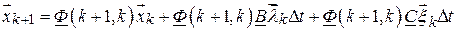где

.

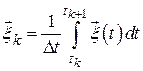Матрица ковариаций составляющих вектора :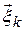

По диагонали полученной ковариационно матрицы расположены величины, равные дисперсиям отдельных составляющих вектора :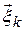

.

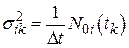Если матрица 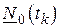принята диагональной, то составляющие процесса 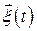некоррелированы между собой.

Совокупности нормальных случайных последовательностей чисел с заданными дисперсиями и нулевым средним легко формируются на ЭВМ с помощью специальных подпрограмм.

Аналогично представим в случае, когда 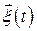- белый шум. Дискретную модель входного случайного воздействия 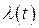, соответствующую выходному процессу формирующего фильтра и описываемую уравнениями (2.83) и (2.84), запишем в виде

.

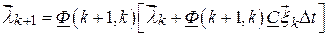Дата добавления: 2014-12-26